Метод Гаусса

Метод Гаусса, его еще называют методом гауссових исключений, состоит в том, что систему линейных алгебраических уравнений

относительно неизвестных , , …, сводят последовательными исключениями неизвестных к эквивалентной системе стреугольной матрицей:

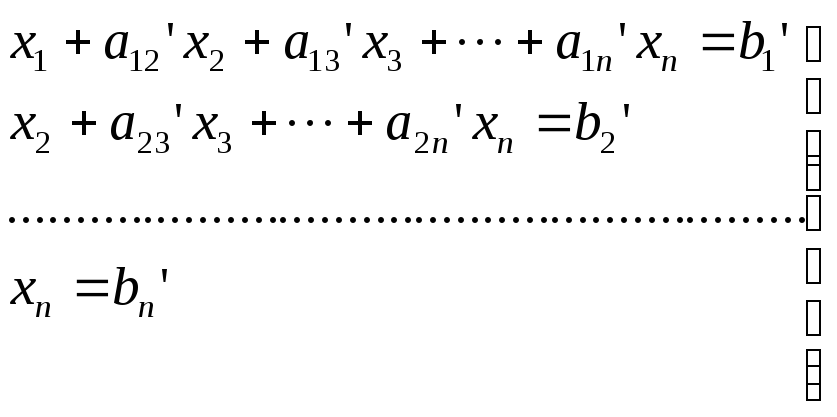
(5

Процесс сведения исходной системы к эквивалентной форме называется прямым ходом метода Гаусса. Прямой ход метода Гаусса выполняется с помощью аппарата элементарных преобразований. Заметим, что в данном случае элементарные преобразования применяются только для строк исходной системы. С другой стороны, необходимо отметить, что, если в исходной системе матрица коэффициентов невырождена, то такую систему уравнений к треугольной форме сводят всегда.

Обратный ход метода Гаусса состоит непосредственно в определении корней системы уравнений, которые находят по рекуррентным соотношениями

;.

Для удобства вычислений элементарные преобразования исходной системы выполняют относительно ее матричной формы. Поэтому записывают расширенную матричную систему

.

Далее прямым ходом метода Гаусса сводят ее к виду:

.

На основании такой матрицы записывают эквивалентную систему уравнений и, используя рекуррентные соотношения, определяют корни исходной системы. Проиллюстрируем применения аппарата метода Гаусса для конкретного примера.

Задача 1.8.Методом Гаусса решить систему линейных алгебраических уравнений

Решение

Запишем расширенную матрицу коэффициентов системы и с помощью элементарных преобразований над строками сведем ее к треугольной форме.

.

Таким образом, прямой ход метода Гаусса завершен. Для реализации обратного хода на основе последней матрицы запишем эквивалентную систему к заданной.

Реализуя обратный ход метода Гаусса, определяютнепосредственно корни исходной системы. В самом деле, из последнего соотношения эквивалентной матрицы значит, что . После подстановкив предпоследнее уравнение имеем

;

В конце концов, из первого равенства имеем:

; .

Итак, исходная система имеет решение:

; ;.

Тема 1.3. Общее исследование систем линейных алгебраических уравнений

При решении систем линейных алгебраических уравнений довольно часто может оказаться, что определитель матрицы коэффициентов системы превращается в нуль или число уравнений не равняется числу неизвестных , то есть . В связи с отмеченным, необходимо заметить, что решение любой системы линейных алгебраических уравнений должно начинаться из выяснения вопроса о ее совместности. Итак, решению системы уравнений должны предшествовать исследования, которые проводятся по такой схеме:

1. Исследовать, является исходная система уравнений совместной или несовместной (то есть, имеет ли исходная система решения вообще).

2. Если исходная система совместная, то необходимо исследовать, имеет такая система единственное решение или их бесчисленное множество.

3. Если система совместная и имеет единственное решение, то определить его известными методами.

4. Если совместная система имеет бесчисленное множество решений, то необходимо описать всю совокупность решений.

Пусть задан общий вид системы линейных алгебраических уравнений с неизвестными

(1.4)

Вопрос о совместности СЛАУ определяется теоремой Кронекера–Капелли. В отличие от теоремы Крамера, эта теорема не является конструктивной, поскольку она не дает соотношений для определения корней системы уравнений. Тем не менее, она имеет очень важное практическое значение.