
01 случайные события / 05_геометрическое представление событий
.doc§5. Геометрическое представление событий и их вероятностей.
Диаграммы Эйлера.
Новые определения.
Многие задачи, связанные со случайными событиями и с подсчетом вероятностей случайных событий гораздо удобнее и проще решать, если пользоваться изложенными в этом параграфе методами – геометрическим представлением событий. Метод был предложен Леонардом Эйлером.
Все
возможные исходы опыта будем изображать
точками единичного квадрата (квадрата
со стороной, равной единице).
Исходы,
благоприятствующие событию
А – точками
области А.
 Изобразим
достоверное
и невозможное
события.
Изобразим
достоверное
и невозможное
события.

По классическому определению для подсчета вероятности нужно подсчитывать количество исходов: благоприятствующих А, и всех возможных.
Геометрически исходы изображаются точками. Измерить количество точек можно площадью. Поэтому общее количество исходов интерпретируем как площадь квадрата (равна 1). Количество исходов, благоприятствующих событию А – площадью круга А. Вероятность события – это отношение этих двух площадей:
( 12
)![]()
Чем больше у события благоприятствующих исходов, тем больше точек включается в круг А, тем больше его площадь, т.е., вероятность события. Максимально возможная площадь – это площадь всего квадрата, т.е. единица.
Изобразим операции над событиями: сумму и произведение.
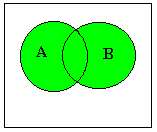
Сумма ( она же объединение ) событий А и В включает в себя все исходы, принадлежащие А (при них появляется событие А)
и все исходы, принадлежащие В
(при них появляется событие В)
объединение исходов
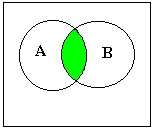
Произведение ( оно же пересечение ) событий А и В включает в себя все исходы, принадлежащие
обоим событиям А и В одновременно.
пересечение двух множеств исходов
Это наглядное представление очень облегчает решение многих задач и позволяет анализировать свойства вероятностей. Мы будем его постоянно использовать, когда будем строить формулы для:
-
вероятностей суммы событий и
-
вероятностей произведения событий
А сейчас рассмотрим примеры:
Пример 1:
Опыт – извлечение одной карты из колоды.
С
Событие В – появление туза черной масти
Что представляют собой события: A + B, A · B ?
И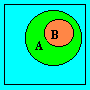 зобразим
геометрически множества исходов каждого
события, учитывая, что событие B
зобразим
геометрически множества исходов каждого
события, учитывая, что событие B
это частный случай события A
Теперь совершенно очевидно, что
A + B = A , A · B = B .
Пример 2:
Используя геометрическое представление событий, определить:
ч
Попробуйте разобрать этот пример самостоятельно. Ответы проверьте, посмотрев в конец параграфа.
Дадим несколько новых определений:

Пример 1:
О
События: А – появление герба, В – появление решки.
События несовместные, они не могут появиться вместе в одном опыте.
Опыт – два человека стреляют в цель.
События: А – попадание 1-го, В – появление попадание 2-го.
События совместные, они могут оба попасть в цель.
Опыт – бросание кубика.
События: А – выпадение четного числа очков.
В – выпадение числа очков, большего четырех.
Выпишем исходы, из которых состоят эти события:
А = { 2, 4, 6 } В = { 5, 6 }
Эти события появятся вместе, если выпадет { 6 } они совместны.
Общее
правило: События
совместны, если у них есть общие исходы.
Если
общих исходов нет, события несовместны.
Геометрическое представление:


О8
События
А1
, А2
, А3
, . . . , Аn
образуют
полную
группу если
в
результате опыта обязательно появляется
хотя бы одно из них.
Это же определение можно записать иначе, формулой:

Левая часть равенства – хотя бы одно событие, правая часть – обязательно.
Пример 1:
Опыт – бросание кубика.
События: А1 – выпадение четного числа очков;
А2 – выпадение числа очков, большего либо равного 5;
А3 – выпадение 1;
А4 – выпадение числа очков, меньшего либо равного 4.
Проверить, образуют ли они полную группу.
Чтобы ответить на этот вопрос нужно выписать исходы, из которых состоят эти события:
А1 = { 2, 4, 6 }
А2 = { 5, 6 }
А3 = { 1 }
А4 = { 1, 2, 3, 4 }
Перебираем по порядку все возможные исходы опыта и проверяем, появляются ли перечисленные выше события:
Выпадает { 1 } – появляются А3 и А4 ;
Выпадает { 2 } – появляются А1 и А4 ;
Выпадает { 3 } – появляется А4 ;
и т.д.
Убеждаемся, что какое бы число ни выпало, обязательно появляется одно или несколько из записанных событий. Значит, эти события образуют полную группу.
Опыт – пытаются поступить на работу в банк два выпускника ДУЭП.
События: А1 – первого из них в банк приняли;
А2 – на работу приняли только одного.
Проверить, образуют ли они полную группу.
В
1 = { + , + } – первого приняли, второго приняли
 2
=
{
+ , – }
– первого
приняли, второго нет, и т.д.
2
=
{
+ , – }
– первого
приняли, второго нет, и т.д.
 3
=
{
– , + }
3
=
{
– , + }
4 = { – , – }
Теперь рассмотрим, из каких исходов состоят заданные события:
А1 = { 1, 2 }
А2 = { 2, 3 }
Убеждаемся, что при появлении исхода ( 4 ) ни одно из записанных событий не происходит. Следовательно, эти события не образуют полную группу.
Замечание
:
Для того, чтобы некоторый набор
событий составлял полную группу,
все
исходы опыта должны быть между этими
событиями распределены.
Геометрическое представление полной группы:

Полная группа
распределены
между событиями Все исходы
опыта

Это же определение тоже можно записать формулами:


О пыт
– бросание кубика.
пыт
– бросание кубика.
События: А – выпадение числа очков, большего 4;
А – выпадение числа очков, меньшего либо равного 4.

Замечание
:
Обычно,
не задумываясь, говорят, что противоположным
к больше
4
будет слово меньше.
Но при
этом теряется один исход:
равно
4.
И тогда
нет полной группы.
Пример 2:
Опыт – бросание точки случайным образом на числовую ось
С обытия:
А
– точка
попадает в область (
-4 ≤ x
< 5 );
обытия:
А
– точка
попадает в область (
-4 ≤ x
< 5 );
А – ( –∞ < x < – 4) или ( 5 ≤ x < + ∞)
Пример 3:

 Событие
B
= A 1·
A
2
+ A
1
·
A
2
.
Событие
B
= A 1·
A
2
+ A
1
·
A
2
.
Что представляет собой событие B ?
Здесь событие B связано с появлением или непоявлением некоторых двух событий A 1 и A 2. Перечислим все возможные исходы, связанные с появлением или непоявлением этих событий:
1 = { + , + } – первое событие появилось, второе появилось;
2 = { + , – } – первое событие появилось, второе нет, и т.д.
3 = { – , + }
4 = { – , – }
Событие B включает в себя исходы 3 и 1 : B = { 3 , 1 }.
В противоположное
B
нужно
включить все
оставшиеся исходы:
противоположное
B
нужно
включить все
оставшиеся исходы:
 B
= {
2
,
4
}
= A
1·
A
2 + A
1 ·
A
2.
B
= {
2
,
4
}
= A
1·
A
2 + A
1 ·
A
2.
.
А теперь пример, который будет очень важным для нас, когда мы будем подсчитывать вероятность суммы событий
Пример 4:
 Событие
B
= A
1+
A
2 + A
3 .
Событие
B
= A
1+
A
2 + A
3 .
Что представляет собой событие B ?
Событие B это сумма, т.е., появление хотя бы одного из слагаемых.
Хотя бы одного – это значит: или одного, или двух, или всех трех.
На долю противоположно события остается один исход:
не появление ни одного.
И так:
B
= A
1·
A
2 ·
A
3
так:
B
= A
1·
A
2 ·
A
3
Выделим особо этот полученный результат. Он нам очень понадобится в дальнейшем:
( 16
)
![]()
Ответ к примеру:
Пример 2:
Используя геометрическое представление событий, определить:
ч
A + U = U, A · U = A,
A + V = A, A · V = V .
Это, кстати означает, что:
событие
U
играет
среди событий ту же роль, что и число
1
среди
чисел,
событие
V
играет
среди событий ту же роль, что и число
0
среди
чисел.
