
- •Матрицы. Операции над матрицами. Матрицы.
- •Виды матриц.
- •Операции над матрицами.
- •Определители квадратных матриц
- •Обратная матрица.
- •Системы линейных уравнений.
- •Метод обратной матрицы.
- •Метод Крамера.
- •Метод Гаусса.
- •Производная.
- •Правила дифференцирования.
- •Производные сложной и обратной функции.
- •Интегрирование.
- •Свойства неопределенного интеграла.
- •Метод замены переменной.
- •Метод интегрирования по частям.
- •Задания для контрольных работ (6 заданий по 25 вариантов)
- •Задание №1
- •Задание №2
Метод замены переменной.
Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой:
![]() ,
,
где
![]() – функция, дифференцируемая на
рассматриваемом промежутке.
– функция, дифференцируемая на
рассматриваемом промежутке.
Пример. Найти
интегралы: а)![]() ;
б)
;
б)![]() ;
в).
;
в).![]()
Решение.
а) Положим
![]() .
Тогда
.
Тогда![]() ,
,
![]() ,
,
![]() .
.
б) Положим
![]() .
Тогда
.
Тогда![]() ,
,![]() и, следовательно,
и, следовательно,
![]() .
.
в) Положим
![]() .
Тогда
.
Тогда![]() .
Так как
.
Так как![]() ,
то
,
то
![]()
![]() .
.
Метод интегрирования по частям.
Пусть
![]() и
и![]() – дифференцируемые функции.Формула
интегрирования по частям
для неопределенного интеграла имеет
вид:
– дифференцируемые функции.Формула
интегрирования по частям
для неопределенного интеграла имеет
вид:
![]() .
.
Формула интегрирования по частям используется для интегралов следующих типов интегралов:
1.
![]() ;
;![]() ;
;![]() .
.
2.
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Пример. Найти
интегралы: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение.
а) Так как
![]() ,
а функция
,
а функция![]() при интегрировании практически не
изменяется (появляется лишь постоянный
множитель) , то данный интеграл можно
найти интегрированием по частям , полагая
при интегрировании практически не
изменяется (появляется лишь постоянный
множитель) , то данный интеграл можно
найти интегрированием по частям , полагая![]() ,
,![]() .
Найдем необходимые для записи правой
части формулы
.
Найдем необходимые для записи правой
части формулы![]() и
и![]() .
.
Так как
![]() ,
то
,
то![]() .
Найдем
.
Найдем![]() :
:
![]() .
.
Теперь, применяя формулу интегрирования по частям, получаем:
![]()
Используя метод
разложения, убеждаемся, что полученный
интеграл – сумма табличного и интеграла,
который был определен при нахождении
![]() .
Таким образом, окончательно
.
Таким образом, окончательно
![]() Замечание.
Анализ
полученного решения показывает, что
постоянная
Замечание.
Анализ
полученного решения показывает, что
постоянная
![]() ,
возникшая при нахождении
,
возникшая при нахождении![]() (по заданному
(по заданному![]() )
не входит в запись окончательного
ответа. Аналогично, в общем случае
постоянная
)
не входит в запись окончательного
ответа. Аналогично, в общем случае
постоянная![]() ,
возникающая при нахождении
,
возникающая при нахождении![]() ,
исключается в процессе решения. Поэтому
в дальнейшем, при интегрировании по
частям и нахождении
,
исключается в процессе решения. Поэтому
в дальнейшем, при интегрировании по
частям и нахождении![]() будем полагать
будем полагать![]() ,
что несколько упрощает запись решения.
,
что несколько упрощает запись решения.
б) Пусть
![]() ,
,![]() .
Тогда
.
Тогда
![]()
и
![]()
Применяя формулу интегрирования по частям , получаем
![]()
![]() .
.
В) Пусть
![]() ,
,![]() .
Тогда
.
Тогда![]() и
и![]() .
Применяя формулу интегрирования по
частям, получаем
.
Применяя формулу интегрирования по
частям, получаем
![]()
![]() .
.
Задания для контрольных работ (6 заданий по 25 вариантов)
Вариант выбирается студентом в соответствии с последними двумя цифрами зачетной книжки. В случае, если две последние цифры превышают 25, то вариант выбирается по формуле: номер зачетки минус необходимое число раз по 25, пока разность не будет меньше или равна 25.
Задание №1
Вычислить матрицу
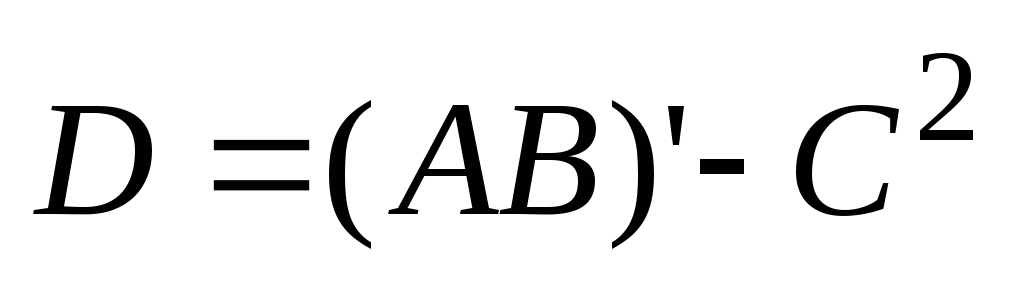 ,
где
,
где ;
; ;
;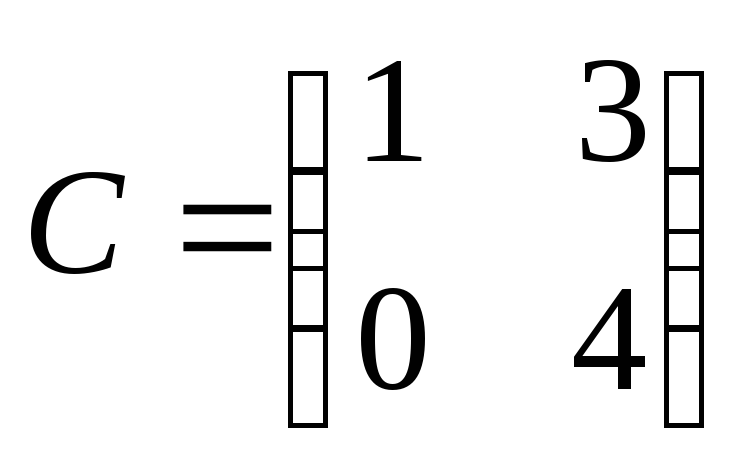 .
.Найти произведение матриц
 ,
где
,
где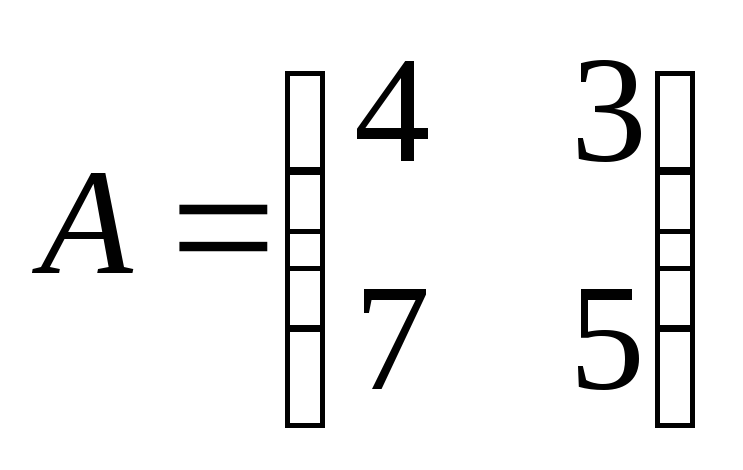 ;
; ;
; .
.Решить уравнение
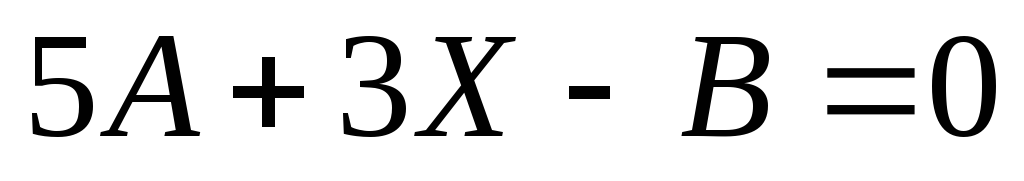 ,
где
,
где ,
, .
.Вычислить матрицу
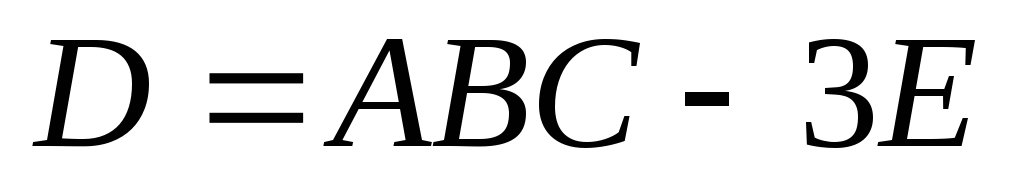 ,
где
,
где
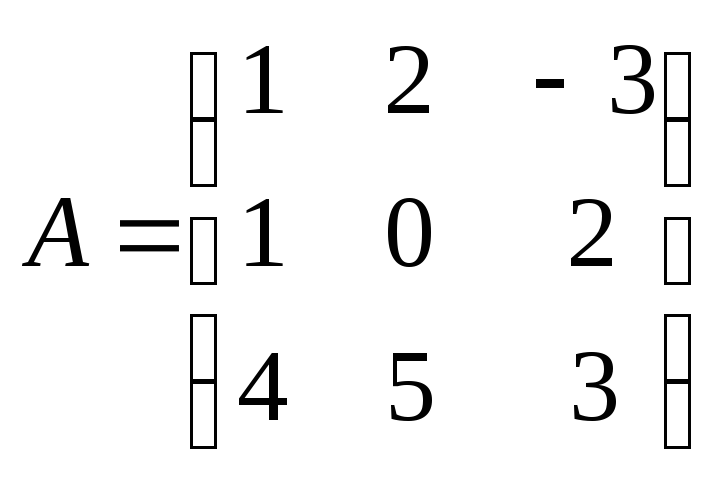 ;
;
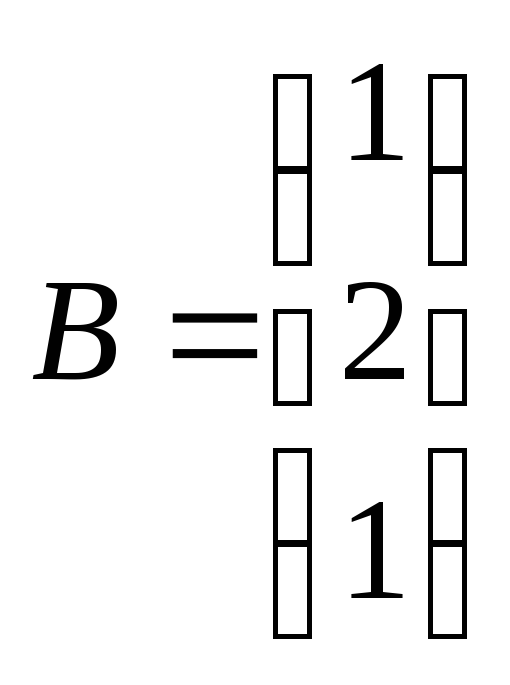 ;
;![]() ;
;![]() – единичная матрица.
– единичная матрица.
Найти произведение матриц
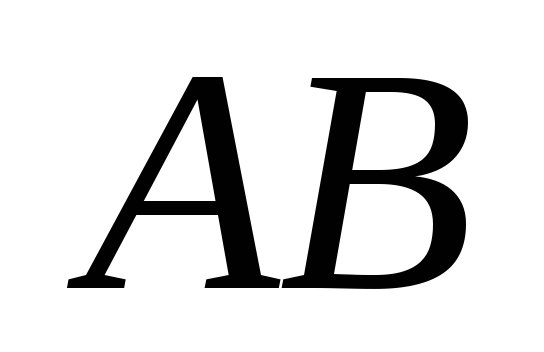 и
и ,
где
,
где
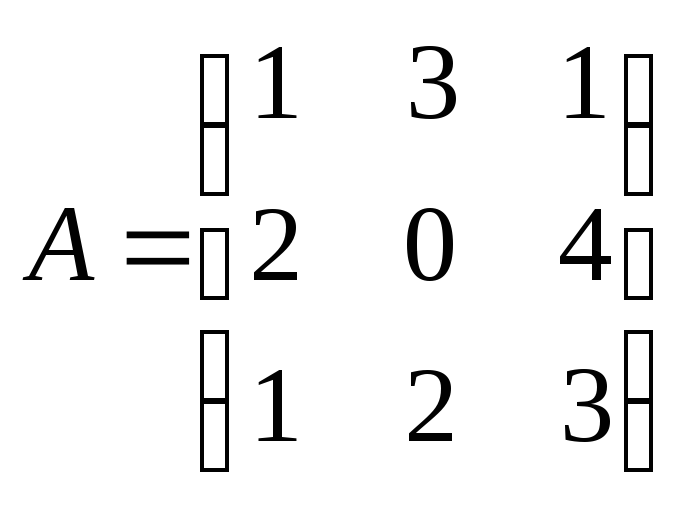 ,
,
 .
.
Найти произведение матриц
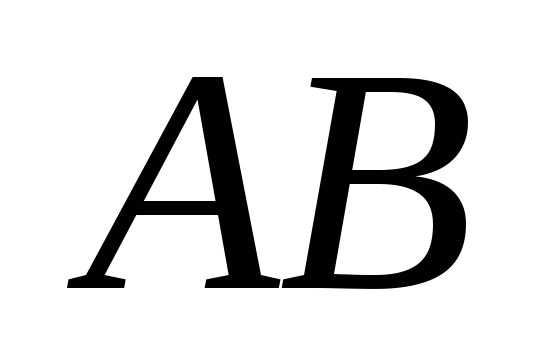 ,
где
,
где
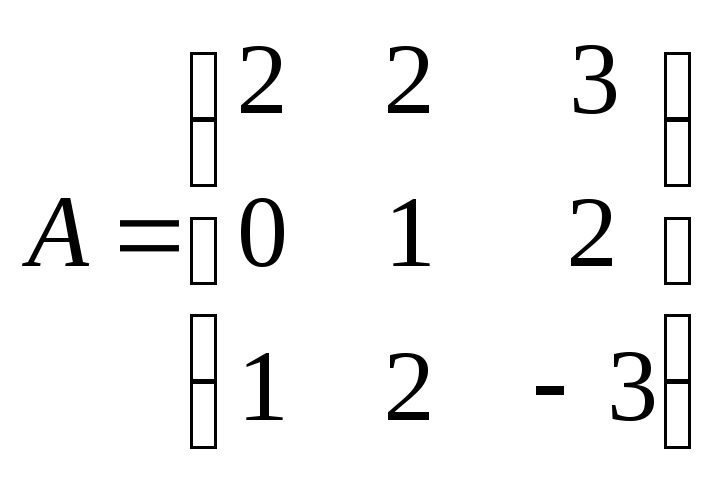 ,
,
 .
.
Найти произведение матриц
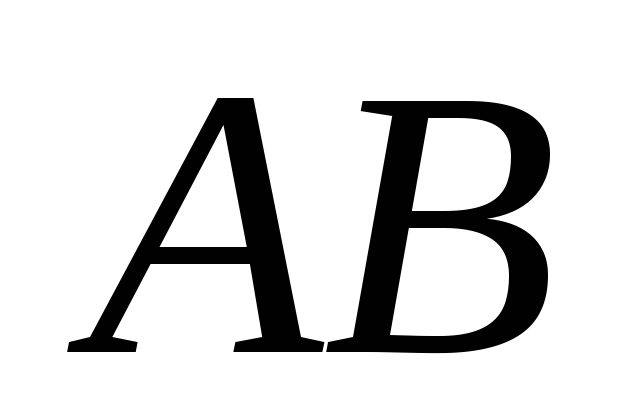 ,
где
,
где ,
,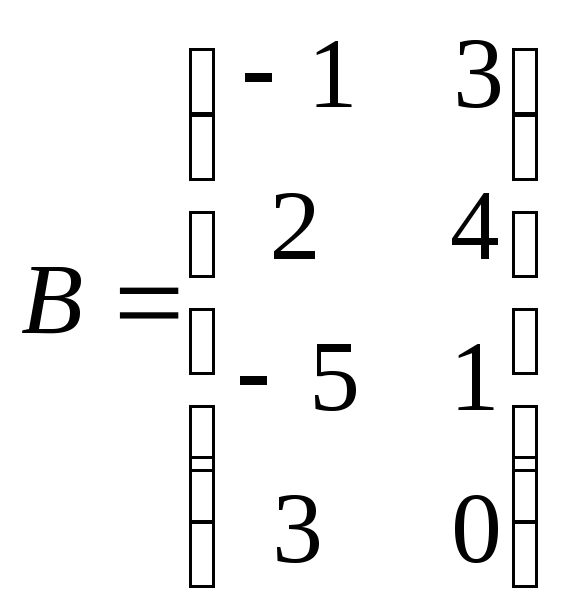 .
.Найти значение матричного многочлена
 ,
если
,
если
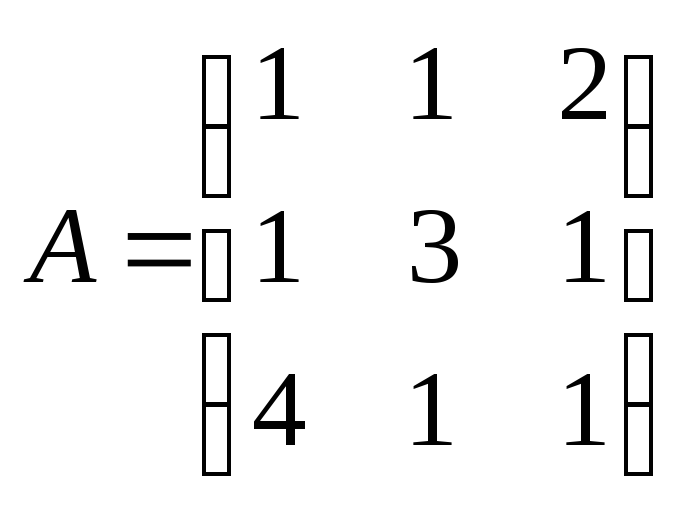 ,
,
![]() – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
Найти произведение матриц
 ,
где
,
где ,
, .
.
10. Найти произведение
матриц
![]() ,
где
,
где ,
,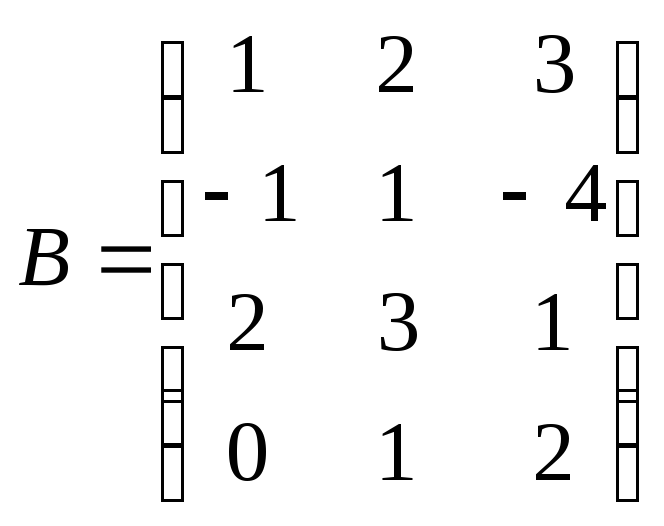 .
.
11. Найти произведение
матриц
![]() ,
где
,
где ,
, .
.
12. Найти значение
матричного многочлена
![]() ,
если
,
если
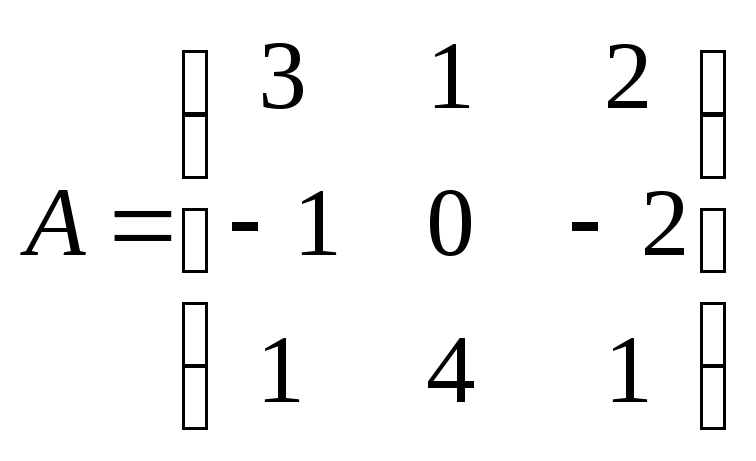 ,
,
![]() – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
13. Вычислить матрицу
![]() ,
где
,
где
 ;
;
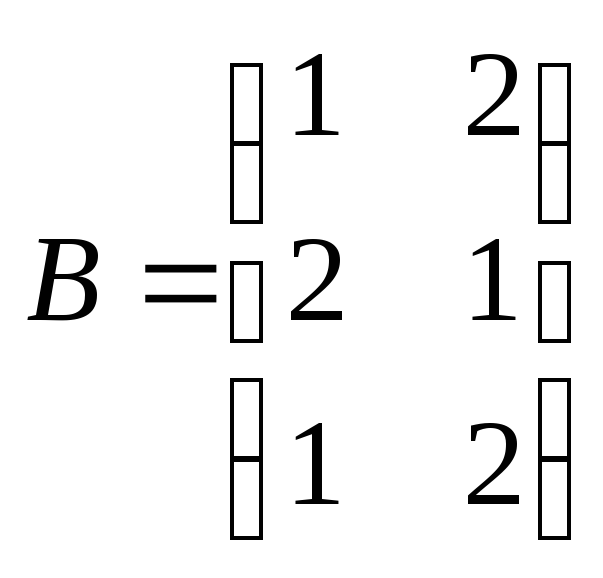 ;
;![]() ;
;![]() – единичная матрица.
– единичная матрица.
14. Решить уравнение
![]() ,
где
,
где ,
, .
.
15. Найти произведение
матриц
![]() ,
где,
,
где,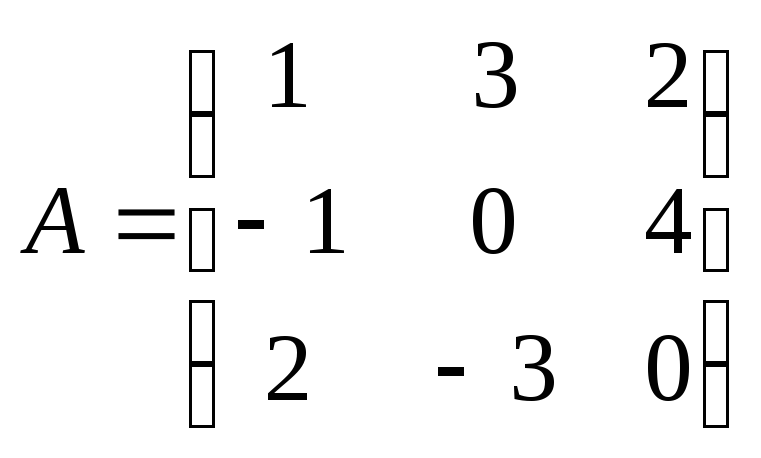 ,
,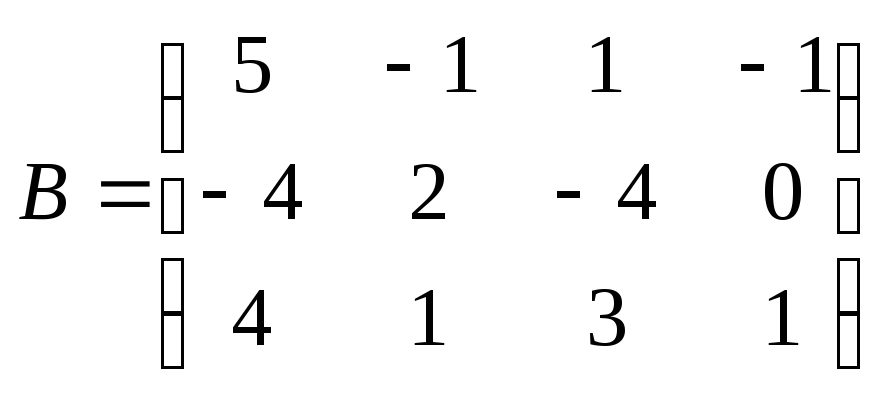 .
.
16. Найти произведение
матриц
![]() ,
где
,
где ,
,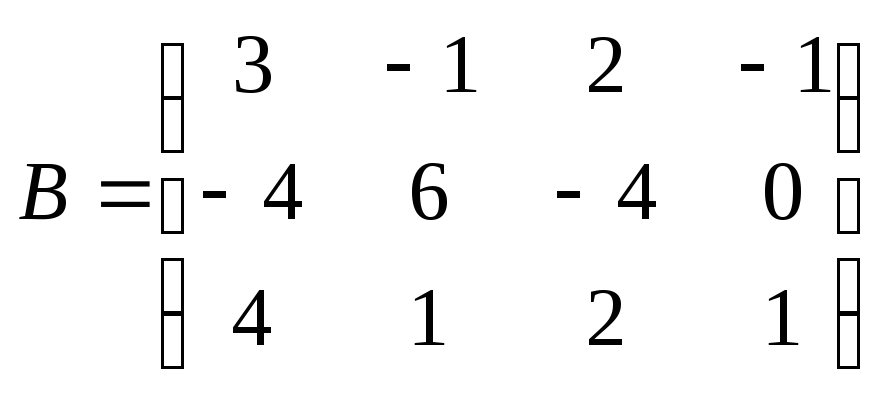 .
.
17. Найти произведение
матриц
![]() ,
где
,
где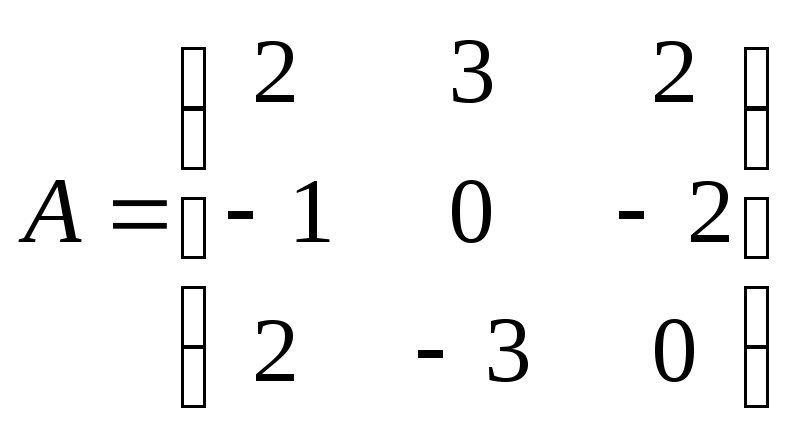 ,
, .
.
18. Найти произведение
матриц
![]() ,
где
,
где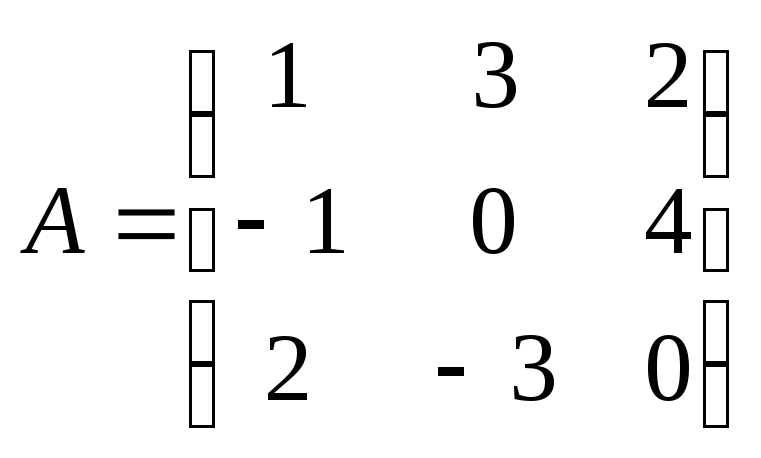 ,
,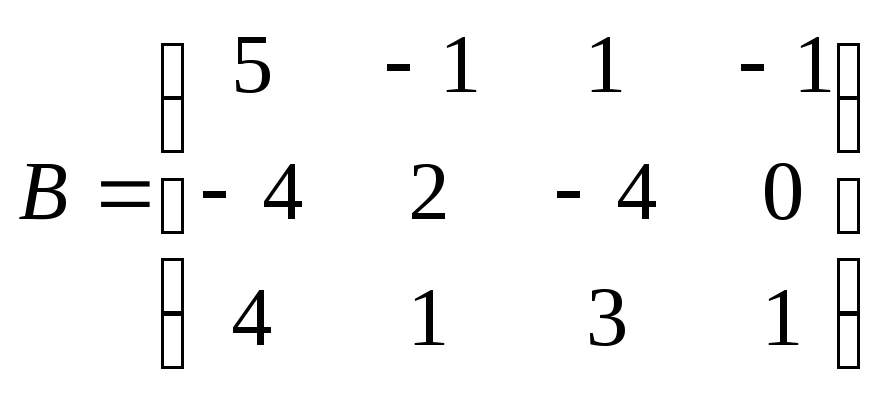 .
.
19. Найти произведение
матриц
![]() ,
где
,
где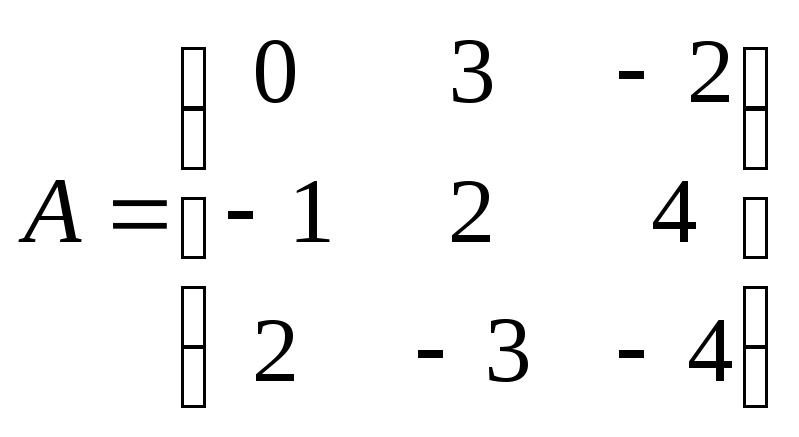 ,
, .
.
20. Найти произведение
матриц
![]() ,
где
,
где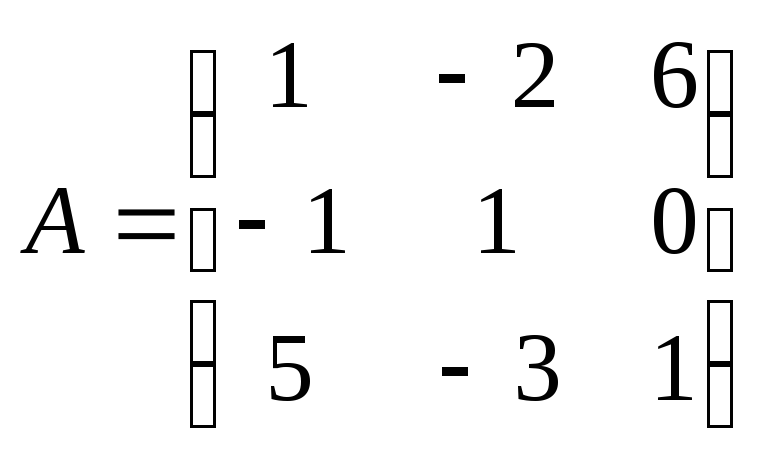 ,
, .
.
21. Найти произведение
матриц
![]() ,
где
,
где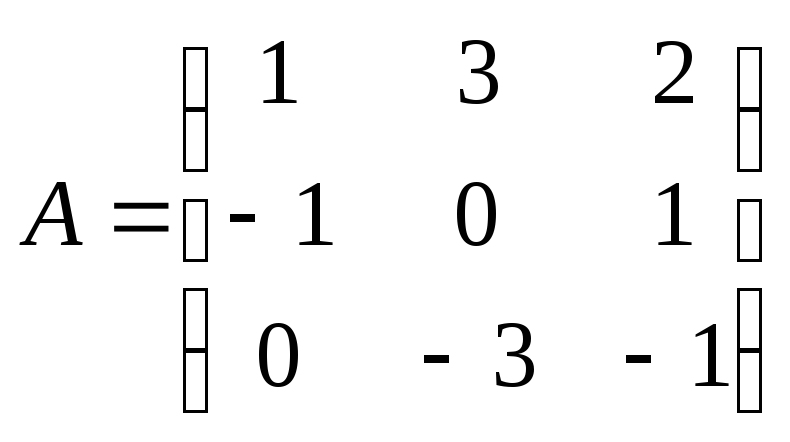 ,
, .
.
22. Найти произведение
матриц
![]() ,
где
,
где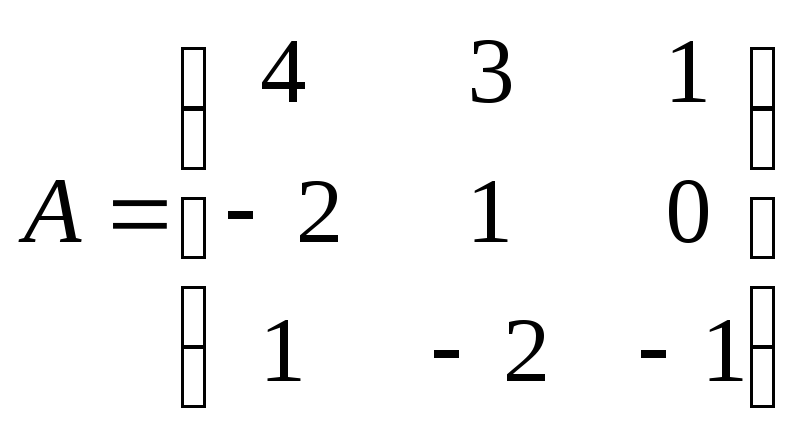 ,
, .
.
23. Найти произведение
матриц
![]() ,
где
,
где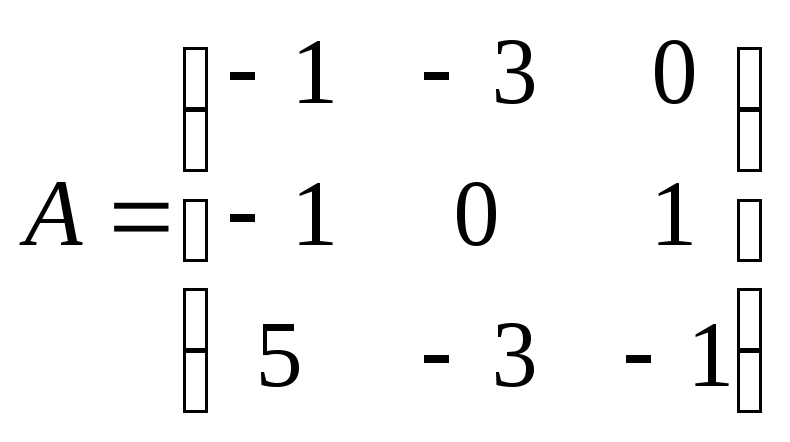 ,
, .
.
24. Найти произведение
матриц
![]() ,
где
,
где ,
, .
.
25. Найти произведение
матриц
![]() ,
где
,
где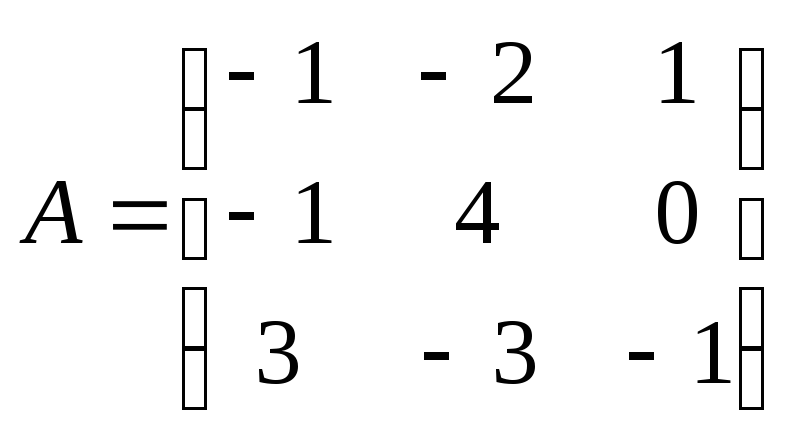 ,
, .
.
