10. Расстояние от точки до прямой.

Для определения расстояния от точки до прямой необходимо знать уравнения прямой и координаты точки в декартовой системе координат. Расстоянием от точки до прямой будет являться перпендикуляр, проведенный из этой точки к прямой.

Инструкция

1

Общее уравнение прямой в декартовых координатах имеет вид Ax+By+C=0, где A, B и C - известные числа. Пусть точка O имеет координаты (x1, y1) в декартовой системе координат.

В этом случае отклонение этой точки от прямой равно δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)), если C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

Расстояние от точки до прямой - это модуль отклонения точки от прямой, то есть r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))|, если C<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

2

Пусть теперь точка с координатами (x1, y1, z1) задана в трехмерном пространстве. Прямая может быть задана параметрически, системой из трех уравнений: x = x0+ta, y = y0+tb, z = z0+tc, где t - действительное число. Расстояние от точки до прямой можно найти как минимальное от этой точки до произвольной точки прямой. Коэффициент t этой точки равен tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2))

3

Расстояние от точки (x1, y1) до прямой можно посчитать и в случае, если прямая задана уравнением с угловым коэффициентом: y = kx+b. Тогда уравнение перпендикулярной ей прямой будет иметь вид: y = (-1/k)x+a. Далее нужно учесть, что эта прямая должна проходить через точку (x1, y1). Отсюда находится число a. После преобразований находится и расстояние между точкой и прямой.

11. Уравнение окружности.

Уравнение окружности ω (A;R) имеет вид (x–a)²+ (y–b)²=R², где a и b – координаты центра A окружности ω (A;R) .

12. каноническое уравнение эллипса.

Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:

                                   .

13.Каноническое уравнение гиперболы.

Теорема. В канонической для гиперболы системе координат уравнение гиперболы имеет вид:

                                   .

14.Директрисы эллипса и гиперболы.

Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии от него, называются директрисами эллипса.

 Уравнения директрис эллипса, заданного каноническим уравнением (*), имеют вид и . Так как для эллипса , то .

 

Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины (рис 8)

Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы.

 

Уравнения директрис гиперболы, заданной каноническим уравнением (**), имеют вид и . Так как для гиперболы , то .

 

Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной (рис. 9).С помощью понятий директрисы и эксцентриситета можно сформулировать общее свойство, присущее эллипсу и гиперболе. Имеют место следующие две теоремы.

 

Теорема 1. Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса.

 

Доказательство. Предположим для определенности, что речь идет о фокусе F₁ и правой директрисе.

Пусть M(x; y) – произвольная точка эллипса (см. рис. 8). Расстояние от точки до правой директрисы выражается равенством (10). Из равенств (2) и (4) мы имеем .

Полагая здесь , получаем формулу расстояния от точки M до правого фокуса: (11).Из соотношений (10) и (11) имеем:.

 

 

 

Теорема 2. Если r – расстояние от произвольной точки M гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение есть величина постоянная, равная эксцентриситету гиперболы.

 

Доказательство. Предположим для определенности, что речь идет о фокусе F₁ и правой директрисе. Пусть M(x; y) – произвольная точка гиперболы (см. рис. 9).Нам придется рассмотреть два случая. 

1). Точка M находится на правой ветке гиперболы. Тогда расстояние от точки M до правой директрисы выражается равенством (12).

Далее, . Полагая здесь , получаем формулу расстояния от точки M до правого фокуса: . Из соотношений (12) и (13) имеем .

 

 

2). Точка M находится на левой ветке гиперболы. Тогда расстояние от точки M до правой директрисы выражается равенством .

Так как , то полагая здесь , получаем формулу расстояния от точкиM до правого фокуса: . Из соотношений (14) и (15) имеем: .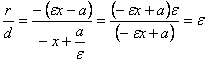

 

 

Выявленное свойство эллипса и гиперболы можно положить в основу общего определения этих линий:

Множество точек, отношение расстояний которых до фокуса и до соответствующей директрисы есть величина постоянная, равная , есть эллипс, если ; есть гипербола, если .

Естественно возникает вопрос, что представляет собой множество точек, определенное аналогичным образом, но при условии . Оказывается, это есть новая линия второго порядка, называемаяпараболой. 

15. Каноническое уравнение параболы : 

у2=2рх