1Теоретичні відомості
1.1 Генеральна сукупність та вибіркова сукупність
Вибіркова сукупність це частина генеральної сукупності, що відображає та відтворює основні характеристики останньої і є її зменшеною моделлю. Вибіркоюназивають сукупність випадково відібраних об’єтків.
Нехай
з генеральної сукупності взята вибірка
, причому
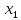 спостерігалося
спостерігалося разів,
разів,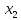 -
-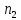 разів
разів
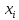 -
-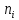 разів.Об’ємом
вибірки називається число об’єктів
цієї сукупності.Спостерігаючі значення
разів.Об’ємом
вибірки називається число об’єктів
цієї сукупності.Спостерігаючі значення
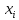 називають варіантами, а частота – це
числа які показують скільки разів
повторюються окремі значення варіант.
називають варіантами, а частота – це
числа які показують скільки разів
повторюються окремі значення варіант.
Накопичена частота одержується послідовним додаванням частот чергового інтервалу, починаючи з першого і закінчуючи останнім. Існують малі та великі вибірки.Відносна частота –це відношення відповідної частоти до об’єму вибірки.Малою називається вибірка яка містить менше ніж 30 елементів.
Великою називається вибірка яка складається більше ніж з 30 елементів, а для соціальних явищ більше ніж 60.
Вибірка володіє наступними властивостями:
об’ємність(чим більший об’єм вибірки, тим точніший результат);
представницькість;
репрезентативність.
Методи відбору:
повторний;
безповторний
Способи відбору:
випадковий відбір(повторний,безповторний);
механічний відбір;
груповий відбір.
Повторною називають вибірку, при якій оброблений об’єкт (перед відбором наступного) повертається в генеральну сукупність.
Безповторною називають вибірку, при якій оброблений об’єкт у генеральну сукупність не повертається.
Механічним називають відбір, при якому генеральну сукупність “механічно” ділять на стільки груп, скільки об’єктів повинно увійти у вибірку, а з кожної групи відбирають один об’єкт або коли з генеральної сукупності береться елемент з певним періодом.
Груповоюназивають вибірку, при якій вибирається група об’єктів підряд починаючи з наперед заданого обсягу.
1.2 Статистичний ряд
Ранжований ряд – це ряд в якому значення ознаки розташовується в зростаючому(спадаючому порядку) і рахунок ведеться за групами.
Статистичний ряд– це таблиця з двох рядків у першому записані значення показників вибірки (варіанта) , в другому відповідна частота появи варіанти.
Інтервальний ряд – це ряд в якому варіанти задаються інтервалами.Використовується для полегшення обробки статистичної інформації на великих вибірках, та у випадках коли частоти варіант мало відрізняються між собою а варіанти розташовані близько одна до одної. Кількість інтервалів визначається за формулою Стреджерса(1.1).
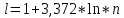 (1.2)
(1.2)
Довжина інтервалу розраховується за формулою:
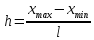 ,
(1.3)
,
(1.3)
де
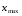 –
максимальне значення варіанти;
–
максимальне значення варіанти;
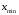 –мінімальне
значення варіанти;
–мінімальне
значення варіанти;
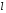 –кількість
інтервалів.
–кількість
інтервалів.
Примітка:
так як
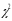 не можна застосовувати, якщо частота
на інтервалі менше 5, то такі інтервали
відкидалися і вибірка знову билася на
інтервали, або зменшувалася кількість
інтервалів.
не можна застосовувати, якщо частота
на інтервалі менше 5, то такі інтервали
відкидалися і вибірка знову билася на
інтервали, або зменшувалася кількість
інтервалів.
3.3 Емпірична функція, властивості
Емпірична
функція розподілу
- це
функція F*(x)
, яка визначає для кожного значення х
відносну частоту події Х<x
, де Х-
деяка кількісна досліджуваного явища.
Таким чином F*(x)=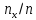 , де
, де
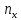 -
число варіант менших х;n-
об’єм
вибірки. На відмінно від емпіричної
функції розподілу вибірки, функція
розподілу F(x)
для генеральної сукупності називають
теоретичною функцією розподілу.
-
число варіант менших х;n-
об’єм
вибірки. На відмінно від емпіричної
функції розподілу вибірки, функція
розподілу F(x)
для генеральної сукупності називають
теоретичною функцією розподілу.
Запис емпіричної функції має наступний вигляд:
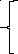
0,
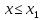
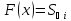 ,
,
 (1.4)
(1.4)
1
,
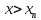
де
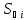 е–
накопичена відносна частота;
е–
накопичена відносна частота;
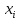 –значення
варіанти.
–значення
варіанти.
 ,
(1.5)
,
(1.5)
де
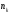 –
частота варіанти;
–
частота варіанти;
 –об’єм
вибірки.
–об’єм
вибірки.
Властивості емпіричної функції :
Значення емпіричної функції належать відрізку [0;1]
F*(x)- неспадна функція;
Якщо
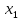 -
найменша варіанта , то F*(x)=0
при х≤
-
найменша варіанта , то F*(x)=0
при х≤ ;
;
Якщо
 -
найбільша
варіанта , то F*(x)=1
при х>
-
найбільша
варіанта , то F*(x)=1
при х>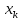 .
.
1.4 Графічне представлення інтервальних рядів
Полігоном частот називають ламану, відрізки якої з'єднують точки
(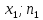 ),
(
),
( ),
(
),
(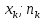 ).
).
У випадку неперервної ознаки доцільно будувати гістограму, для чого інтервал, в якому містяться всі спостережені значення ознаки, розбивають на декілька часткових інтервалів і знаходять для кожного часткового інтервалу підсуму частот варіант, що попали в і-тий інтервал.
Гістограмою частот називають східчасту фігуру, що складається із прямокутників, основами яких слугують часткові інтервали довжиною h, а висоти дорівнюють відношенню ni/h (густина частот). Площа гістограми частот дорівнює об'єму вибірки.
Гістограмою накопичення частот називають ступінчасту фігуру, яка складається з прямокутників, основи яких дорівнюють довжинам інтервалів. Висота прямокутників дорівнює частоті значень для кожного окремого інтервалу. Значення йдуть по накопиченню. На осі абсцис відкладаються довжини інтервалу, а на осі ординат відкладаються накопичені частоти значень.
Графік
функції розподілу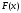 у загальному випадку представляє собою
графік неспадної функції, значення якої
починаються з 0 і доходять до 1, причому
в окремих точках функція має розриви
(стрибки).
у загальному випадку представляє собою
графік неспадної функції, значення якої
починаються з 0 і доходять до 1, причому
в окремих точках функція має розриви
(стрибки).
1.5 Числові характеристики варіаційних рядів
Простою середньоарифметичною вибірки називають суму варіант вибірки, поділену на об’єм вибірки.
 ;
(1.6)
;
(1.6)
Дисперсія середнє арифметичне квадратів відхилення варіант від їх середнього.
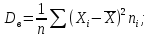 (1.7)
(1.7)
Середнє квадратичне відхилення – квадратний корінь з дисперсії.
 ;
(1.8)
;
(1.8)
Коефіцієнт варіації – характеристика однорідності вибірки (генеральної сукупності) і обчислюється за формулою:
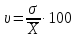 .
(1.9)
.
(1.9)
Мода значення варіанти, яка має найбільшу частоту.
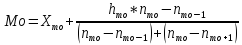 ,
(1.10)
,
(1.10)
де -
початок
модального інтервалу;
-
початок
модального інтервалу;
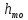 –
довжина
модального інтервалу;
–
довжина
модального інтервалу;
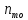 –
частота
модального інтервалу
–
частота
модального інтервалу
 –
частота
інтервалу, що передує модальному;
–
частота
інтервалу, що передує модальному;
 –
частота
інтервалу, що після модального;
–
частота
інтервалу, що після модального;
для обчислення моди використаємо наступну формулу:
Медіана– значення варіанти, яке ділить вибірку(сукупність) навпіл.
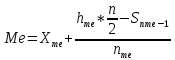 ,
(1.11)
,
(1.11)
де
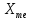 -
початок медіанного інтервалу;
-
початок медіанного інтервалу;
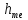 – довжина
медіанного інтервалу;
– довжина
медіанного інтервалу;
 – об’єм
вибірки;
– об’єм
вибірки;
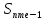 – накопичена
частота інтервалу, що передує медіанному;
– накопичена
частота інтервалу, що передує медіанному;
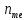 –частота
медіанного інтервалу;
–частота
медіанного інтервалу;
Асиметрія – безрозмірна величина, яка показує ступінь скошеності вибірки і обчислюється за формулою
 ,або
,або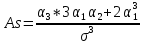 ;
(1.12)
;
(1.12)
де
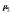 – центральний момент третього порядку;
– центральний момент третього порядку;
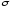 –середнє
квадратичне відхилення.
–середнє
квадратичне відхилення.
Ексцес – безрозмірна величина, яка показує характер гостроверхостіі обчислюється за формулою
 ,
,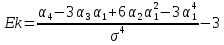 (1.13)
(1.13)
де
 – центральний момент четвертого порядку;
– центральний момент четвертого порядку;
 –середнє
квадратичне відхилення.
–середнє
квадратичне відхилення.
Похибки бувають абсолютні та відносні. Абсолютна похибка вимірювання це похибка вимірювання, виражена в одиницях вимірюваної величини.
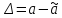 (1.14)
(1.14)
Відносна похибка вимірювання – це похибка вимірювання, виражена як відношення абсолютної похибки до дійсного відношення абсолютної похибки. Відносну похибку знаходять за співвідношенням:
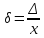 ,
або
,
або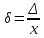 *100%
(1.15)
*100%
(1.15)
1.6Статистичні гіпотези
Глибокий статистичний аналіз включає порівняння різних критеріїв (коефіцієнтів) та перевірку гіпотез про їх істотність для більш повного розуміння результатів. Розглянемо трохи докладніше, як саме проходить процес перевірки статистичних гіпотез. Під гіпотезою в статистиці розуміють припущення про розподіл випадкової величини. Так гіпотезою є припущення, що деякий розподіл (наприклад, за віком тощо) має середнє значення 20. Або при розв’язуванні задач, які полягають в оцінці різниці між результатами, одержаними під час різних експериментів.
Критерій
перевірки гіпотези надає метод перевірки,
в результаті якого з’ясовується, вірна
чи невірна дана гіпотеза, тобто
«приймається» вона чи «відкидається1’.
Якщо відхилення експериментальних
даних від гіпотези мале і є випадковим
– гіпотеза приймається, якщо ж це
відхилення не можна вважати випадковим
і мова йде про так зване істотне відхилення
– гіпотеза відхиляється. Отже суть
перевірки гіпотез полягає у тому, щоб
визначити, узгоджуються чи ні результати
експерименту з гіпотезою, випадковими
чи не
випадковими є розбіжності між
гіпотезою і даними вибіркового обстеження.
Гіпотеза, відхилення від якої приписують
випадку, називається нульовою і
позначається
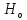 .
Кожній нульовій гіпотезі протиставляють
альтернативну
.
Кожній нульовій гіпотезі протиставляють
альтернативну .
.
Статистична
перевірка гіпотез неминуче пов’язана
з ризиком прийняття помилкового рішення.
Ризик І–помилка першого роду–відхилення
правильної нульової гіпотези. Ймовірність
зробити таку помилку дорівнює
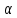 .
Ризик II–помилка другого роду–нульова
гіпотеза приймається (невідхилення
Но). Хоча насправді правильною є
альтернативна. Ймовірність зробити цю
помилку дорівнює 1 – β, де β – ймовірність
того, що помилка II роду не буде зроблена
– так звана потужність критерію.
Ці ризики конкуруючі, і зменшення
ймовірності одного (α) зумовлює збільшення
ймовірності іншого (β).
.
Ризик II–помилка другого роду–нульова
гіпотеза приймається (невідхилення
Но). Хоча насправді правильною є
альтернативна. Ймовірність зробити цю
помилку дорівнює 1 – β, де β – ймовірність
того, що помилка II роду не буде зроблена
– так звана потужність критерію.
Ці ризики конкуруючі, і зменшення
ймовірності одного (α) зумовлює збільшення
ймовірності іншого (β).
Правило за яким гіпотеза Но відхиляється або не відхиляється (приймається), називається статистичним критерієм (функцією критерію). Значення характеристики має певну ймовірність. Межу малоймовірності називаютьрівнем істинності а – це ймовірність ризику І, тобто ймовірність відхилення вірної Н0 (помилки першого роду), а тому залежно від змісту гіпотези Но і наслідків її відхилення рівень істотності визначають у кожному конкретному дослідженні. Звичайно вибираютьодин з рівнів α, для яких існують табульовані значення статистичних характеристик критеріїв:
α = 0.10; 0.05; 0.025;0.01.
Під критичними значеннями статистичної характеристики розуміють теоретичні (табличні) її значення, обчислені для певного розподілу і з відповідним рівнем істотності (ймовірності) та ступенів вільності (чисел, що показують різницю між кількістю різних дослідів [спостережень] та кількістю констант к [параметрів, що оцінюються], знайдених завдяки цим дослідам незалежно один від одного.
Поняття ступені вільності – одне з найбільш важливих понять статистики. Це питання досить важке для розуміння, тому для його пояснення обмежимося спрощеним трактуванням, у відповідності з яким для сукупності спостережень, що розглядається, число ступенів вільності співпадає з числом незалежних одне від одного спостережень.
1.7 Перевірка гіпотез за двома критеріями
Початкові та центральні емпіричні моменти є обґрунтованими оцінками відповідно початкових та центральних теоретичних моментів того ж порядку. На цьому оснований метод моментів, який був запропонований Пірсоном. Перевага методу – його відносна простота. Метод моментів точкової оцінки невідомих параметрів заданого розподілу полягає в прирівняні теоретичних моментів розглядуваного розподілу до відповідних емпіричних моментів того ж порядку.
 -критерійПірсонапризначенийдля
співставлення емпіричного розподілу
з теоретичним,для співставлення двох
і більше емпіричних розподілів.
-критерійПірсонапризначенийдля
співставлення емпіричного розподілу
з теоретичним,для співставлення двох
і більше емпіричних розподілів.
Суть критерію:
Критерій
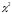 відповідає на питання “Чи з однаковою
частотою зустрічаються різні значення
ознаки?” Критерій дозволяє співставляти
ознаки по будь-якій шкалі.
відповідає на питання “Чи з однаковою
частотою зустрічаються різні значення
ознаки?” Критерій дозволяє співставляти
ознаки по будь-якій шкалі.
Обмеження критерію:
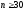 ;
;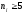 ;
;вибрані варіанти повинні охоплювати весь діапазон варіативності ознаки, при цьому групування повинно бути однаковим у всіх розподілах, що співставляються;
групування повинно містити рівні інтервали (значення ознаки мають бути рівновіддалені).
Нульова гіпотеза: емпіричний закон розподілу відповідає теоретичному
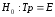 .
.
Альтернативна гіпотеза: емпіричний закон розподілу не відповідає теоретичному
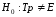 .
.
Емпіричне
значення
 розраховується за формулою:
розраховується за формулою:
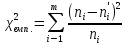 .
(1.16)
.
(1.16)
Далі
по таблиці критичних точок ,
за заданим рівнем значущості
,
за заданим рівнем значущості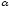 і кількості ступенів свободи
і кількості ступенів свободи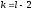 ,
знаходять критичну точку.
,
знаходять критичну точку.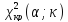
Якщо ,
то підстав відхилити нульову гіпотезу
немає. Якщо
,
то підстав відхилити нульову гіпотезу
немає. Якщо
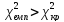 -
нульову гіпотезу відхиляють.
-
нульову гіпотезу відхиляють.
Критерій Колмогорова - Смірнова
Критерій ґрунтується на порівнянні статистичної і теоретичної функцій розподілу. Якщо
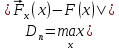 ,
(1.17)
,
(1.17)
то при n→∞
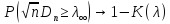 ,
(1.18)
,
(1.18)
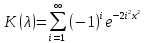 ,𝜆>0.
(1.19)
,𝜆>0.
(1.19)
За допомогою таблиць розподілу Колмогорова - Смірнова визначається правостороння критична область.
2 Послідовність виконання роботи
2.1 Побудова вибірок з генеральної сукупності
Для висунення гіпотез про можливий вид розподілу ми виконали наступні завдання:
Побудовали вибіркові сукупності із генеральної.
Для формування безповторної вибірки ми завантажили файл «Бесповторная.xls», включивши МАКРОСИ, і скористатися командою меню Сервіс \ Макрос \ Макроси.\ Вибірка без повторів та вказуємо діапазони вхідних і вихідних комірок. Для формування вибірки з повторенням було виконано такі команди: Дані/ Аналіз даних/ Вибірка. Для формування вибірки механічним відбором: Дані/ Аналіз даних/ Вибірка . Велику вибірку (200 ел.) методом групового відбору, починаючи з 24 числа відбираємо 200 елементів, а малу беремо 25 елементів, починаючи з 24 числа. Дані беремо з додатку А (таблиця 1).
Отримані ранжовані вибірки наведено в (таблиці А. 2-9)
2.2Побудова інтервальних варіаційних рядів та обчислення емпіричної функції
Для подальших досліджень дані ранжованих вибірок було згруповано у інтервальні ряди.
Для визначення частот варіант використано функцію Microsoft Excel “Частота”. Отримані інтервальні ряди представлено в таблицях В.1 – 4.
За умовою, частота інтервала не повинна бути меншою 5. Оскільки у наших вибірках такі частоти були присутні, то ми відкидали ту кількість елементів, які входять до інтервалів,частоти яких менші 5. Межа відкидання становить 20 %, тобто 40 елементів. Але якщо і при таких змінах значення частот були менші за 5, то ми зменшували кількість інтервалів.
У нашому випадку: для великої безповторної вибірки було відкинуто 35 ел. і кількість інтервалів зменшена до 12; для великої повторної вибірки – 34 ел. і кількість інтервалів – 12; для великої механічної вибірки – 19 ел. і кількість інтервалів – 14; для великої групової вибірки – 15 ел. і кількість інтервалів – 12.(таблиці С.1– 9).
Емпірична функція (С.1–8).
2.3 Побудова гістограм частот, полігонів частот, гістограм накопичених частот та графіків емпіричної функції
За допомогою команди меню Вставка \ Диаграмма було побудовано в MicrosoftExcel гістограму, полігон, графік емпіричної функції розподілу , які представленні в додатку D для кожної вибірки відповідно.
Порівнюючи полігони частот вибірок із полігоном частот генеральної сукупності ми зробили висновок, що полігони частот великих повторної і групової вибірок найкраще відображають генеральну сукупність. Найменш схожими з полігоном частот генеральної сукупності є полігони малих механічної і безповторної вибірок.
На даному кроці на основі візуального порівняння полігонів частот наших вибірок і графіків законів розподілу було висунуто гіпотези про можливий закон розподілу генеральної сукупності.
Проаналізувавши полігон частот можна відкинути рівномірний закон розподілу, адже графік має бути приблизно паралельний осі ОХ, також можна меншу увагу звертати на нормальний та логарифмічно-нормальний закон розподілу, тому що графік полігону частот менш схожий на ці закони розподілу. Отже, дані графіки свідчать про можливість наступних двох розподілів:
Бета-розподілу та Експоненціального розподілу що видно з графіків. Можливість Бета-розподілу наступна, оскільки Бета-розподіл задається через щільність
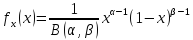 ,
(2.6)
,
(2.6)
де α,β довільні параметри.Графік цього розподілу при α=1 і β=3 дуже схожий на експоненціальний розподіл, тому на даному етапі ми не можемо відкинути даний графік.Спростувати чи навпаки підтвердити дані розподіли ми зможемо після побудови полігону для генеральної сукупності а також елементи вибірки знаходяться в інтервалі[0;1].
Дані графіки знаходяться в додатку D.
2.4 Обчислення числових характеристик
Визначимо для вибіркових сукупностей числові характеристики за формулами (1.6 – 1.13)
Одержимо наступні числові характеристики для всіх вибірок:
Таблиця 2.1 – Зведена таблиця числових характеристик
|
Назва вибірки
Числові хар. |
Г. С |
ВПВ |
ВБВ |
ВМВ |
ВГВ |
МПВ |
МБВ |
ММВ |
МГВ |
сер. Знач |
|
M(x) |
0,109 |
0,064 |
0,065 |
0,085 |
0,093 |
0,094 |
0,083 |
0,105 |
0,104 |
0,068 |
|
D(x) |
0,012 |
0,003 |
0,003 |
0,004 |
0,006 |
0,012 |
0,009 |
0,013 |
0,007 |
0,003 |
|
Середнє кв. |
0,111 |
0,049 |
0,050 |
0,065 |
0,079 |
0,109 |
0,094 |
0,112 |
0,082 |
0,054 |
|
Коефіцієнт варіації |
102% |
76% |
78% |
77% |
85% |
116% |
113% |
107% |
79% |
69% |
|
Мода |
0,011 |
0,013 |
0,014 |
0,201 |
0,138 |
0,050 |
0,046 |
0,041 |
0,183 |
0,083 |
|
Медіана |
0,084 |
0,055 |
0,054 |
0,075 |
0,069 |
0,072 |
0,057 |
0,075 |
0,070 |
0,056 |
|
Асиметрія |
1,769 |
0,612 |
0,655 |
0,501 |
0,765 |
1,734 |
2,049 |
1,861 |
0,619 |
0,554 |
|
Ексцес |
– |
-0,665 |
-0,634 |
-0,936 |
-0,069 |
– |
– |
– |
-0,724 |
-0,498 |
|
Сер. знач. по вибірці |
0,445 |
0,111 |
0,123 |
0,096 |
0,241 |
0,462 |
0,495 |
0,468 |
0,141 |
0,126 |
За візуальною оцінкою було виявлено, що генеральній сукупності із великих вибірок найбільш відповідає велика групова вибірка.
Щоб висунути гіпотези про можливий вид розподілу обчислимо абсолютну та відносну похибки для кожної вибірки.
Знайдемо абсолютну похибку числових характеристик за формулою(1.14).
Таблиця 2. 2 – Абсолютні похибки числових характеристики
|
Назва вибірки Числові хар. , |
ВПВ |
ВБВ |
ВМВ |
ВГВ |
МПВ |
МБВ |
ММВ |
МГВ |
|
M(x) |
0,04443 |
0,044 |
0,0238 |
0,0154 |
0,0143 |
0,0256 |
0,0039 |
0,0045 |
|
D(x) |
0,0097 |
0,0097 |
0,008 |
0,0059 |
0,0003 |
0,0035 |
0,0003 |
0,0055 |
|
Середнє квадратичне |
0,0617 |
0,0602 |
0,0455 |
0,0315 |
0,0015 |
0,0171 |
0,001 |
0,0288 |
|
Коефіцієнт варіації |
26% |
24% |
25% |
17% |
14% |
11% |
5% |
23% |
|
Мода |
0,0023 |
0,0037 |
0,1909 |
0,1277 |
0,0393 |
0,0358 |
0,0304 |
0,1727 |
|
Медіана |
0,0291 |
0,0299 |
0,0093 |
0,0155 |
0,0121 |
0,0272 |
0,0094 |
0,0145 |
|
Асиметрія |
1,1566 |
1,1142 |
1,2683 |
1,0042 |
0,035 |
0,2796 |
0,092 |
1,1498 |
|
Ексцес |
0,6649 |
0,6336 |
0,9361 |
0,0693 |
– |
– |
– |
0,7237 |
Знайдемо відносну похибку за формулою (1.15).
Таблиця 2. 3 – Відносна похибка числових характеристик
|
Назва вибірки
Числові хар. |
ВПВ |
ВБВ |
ВМВ |
ВГВ |
МПВ |
МБВ |
ММВ |
МГВ |
Сер. Знач |
|
M(x) |
0,409 |
0,405 |
0,219 |
0,142 |
0,132 |
0,236 |
0,036 |
0,041 |
0,266 |
|
D(x) |
0,795 |
0,795 |
0,656 |
0,484 |
0,025 |
0,287 |
0,025 |
0,451 |
0,050 |
|
Середнє кВ. |
0,558 |
0,544 |
0,411 |
0,285 |
0,014 |
0,155 |
0,009 |
0,260 |
0,014 |
|
Коефіцієнт варіації |
25% |
24% |
25% |
17% |
14% |
11% |
5% |
23% |
2% |
|
Мода |
0,219 |
0,352 |
18,181 |
12,162 |
3,743 |
3,410 |
2,895 |
16,448 |
0,831 |
|
Медіана |
0,346 |
0,356 |
0,111 |
0,184 |
0,144 |
0,323 |
0,112 |
0,172 |
0,024 |
|
Асиметрія |
0,654 |
0,630 |
0,717 |
0,568 |
0,020 |
0,158 |
0,052 |
0,650 |
0,028 |
|
Ексцес |
– |
– |
– |
– |
– |
– |
– |
– |
– |
|
Сер відносна похибка по вибірці |
0,462 |
0,474 |
2,934 |
1,999 |
0,602 |
0,668 |
0,454 |
2,607 |
0,175 |
Розглянувши похибки великих вибірок можна сказати, що найбільш точною є велика повторна вибірка, а найменш точною – велика механічна вибірка.
4.5 Визначення оцінки параметрів розподілу
Спираючись на результати аналізу , ми можемо впевнитися про припущення щодо можливого виду розподілу. Раніше ми припускали про можливість двох розподілів : експоненціального та Бета – розподілу. З отриманих результатів по генеральній сукупності чітко видно що математичне сподівання та середнє квадратичне майже однакові(таблиця 1)
Отже припущення , що даний розподіл може бути розподілений за Бета-розподілом на даному етапі відхиляємо. І можимо висунути гіпотези:
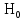 – Розподіл
за яким розподіляються вибіркові
сукупності експоненціальний.
– Розподіл
за яким розподіляються вибіркові
сукупності експоненціальний.
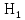 –Розподіл
за яким розподіляються вибіркові
сукупності не експоненціальний
–Розподіл
за яким розподіляються вибіркові
сукупності не експоненціальний
Для визначення оцінки параметрів розподілу використаємо метод моментів. Для експоненціального розподілу в нас всього один параметр λ. Дляе кспоненціально розподіленої випадкової величини функція щільності має вигляд:
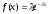
Тобто за допомогою початкового теоретичного моменту та початкового емпіричного моменту. Які рівні між собою, тобто математичне сподівання дорівнює середньому вибірковому.
де
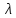 –
точкова оцінка або параметр.
–
точкова оцінка або параметр.
Таблиця 2.4 – Щільність експоненціального розподілу для вибірок.
|
Назва вибірки |
λ |
|
|
ВПВ |
|
|
|
ВБВ |
|
|
|
ВМВ |
|
|
|
ВГВ |
|
|
Після
знаходження параметру
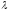 ,
побудуємо графіки щільності для кожної
великої вибірки. Графіки щільності
побудуємо за допомогою надбудов
MicrosoftExcel.
,
побудуємо графіки щільності для кожної
великої вибірки. Графіки щільності
побудуємо за допомогою надбудов
MicrosoftExcel.
Таблиця 2.5 – Щільністьдля великої повторної вибір
|
кількість інтервалів |
f(x) |
|
1 |
2448,816 |
|
2 |
1939,161 |
|
3 |
1535,576 |
|
4 |
1215,987 |
|
5 |
962,9116 |
|
6 |
762,5073 |
|
7 |
603,8117 |
|
8 |
478,1444 |
|
9 |
378,6314 |
|
10 |
299,8294 |
|
11 |
237,4279 |
|
12 |
188,0136 |
Таблиця 2.7 – Щільністьдля великої без повторної вибірки:
|
кількість інтервалів |
f(x) |
|
1 |
2039,4509 |
|
2 |
1611,7301 |
|
3 |
1273,7124 |
|
4 |
1006,5849 |
|
5 |
795,4804 |
|
6 |
628,6494 |
|
7 |
496,8069 |
|
8 |
392,6148 |
|
9 |
310,2742 |
|
10 |
245,2024 |
|
11 |
193,7777 |
|
12 |
153,1380 |
Таблиця 2.8 – Щільність для великої механічної вибірки
|
кількість інтервалів |
f(x) |
|
1 |
2121,4976 |
|
2 |
1748,4833 |
|
3 |
1441,0546 |
|
4 |
1187,6798 |
|
5 |
978,8549 |
|
6 |
806,7468 |
|
7 |
664,8998 |
|
8 |
547,9932 |
|
9 |
451,6417 |
|
10 |
372,2314 |
|
11 |
306,7835 |
|
12 |
252,8430 |
|
13 |
208,3866 |
|
14 |
171,7468 |
Таблиця 2.9 – Щільність для великої групової вибірки
|
кількість інтервалів |
f(x) |
|
1 |
1956,6296 |
|
2 |
1516,1336 |
|
3 |
1174,8065 |
|
4 |
910,3223 |
|
5 |
705,3815 |
|
6 |
546,5789 |
|
7 |
423,5276 |
|
8 |
328,1789 |
|
9 |
254,2960 |
|
10 |
197,0463 |
|
11 |
152,6853 |
|
12 |
118,3112 |
Отримані щільності розподілів зобразимо графічно наклавши їх на відповідні полігони частот. Представлення даних графіків:
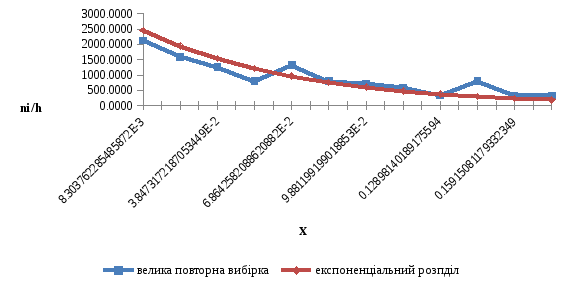
Рисунок 2.1 – Полігон частот великої повторної вибірки та щільність експоненціального розподілу
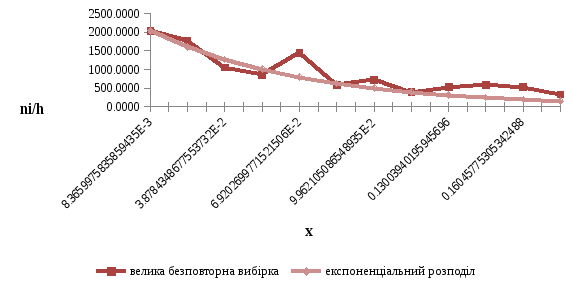
Рисунок 2.2 – Полігон частот великої без повторної вибірки та щільність експоненціального розподілу
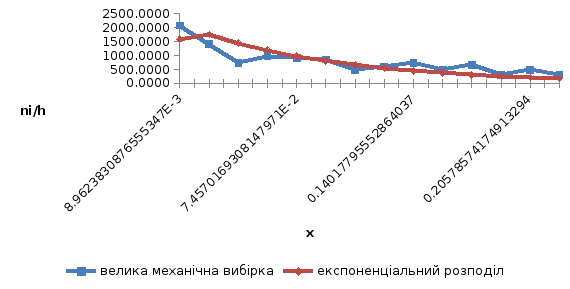
Рисунок 2.3 – Полігон частот великої механічної вибірки та графік щільності експоненціального розподілу
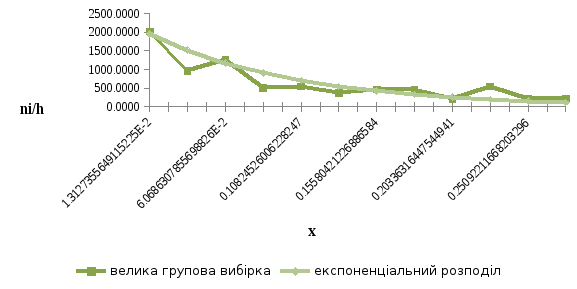
Рисунок 2.4 – Полігон частот великої групової вибірки і графікщільності експоненціального розподілу

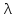 =
15,469
=
15,469
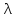 =
15,476
=
15,476
 =11,
79
=11,
79
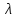 =
10,726
=
10,726