Задача 2

Знайти оптимальний план транспортної задачі за даними таблиці, - матриця вартості перевезення одиниці вантажу;- запаси,- потреби вантажу (у.о.), де;.

Розв’язання:

Знаходимо .

Так як >, то маємо відкриту транспортну задачу (ТЗ). Для перетворення її в закриту ТЗ вводимо фіктивного виробниказ об’ємом виробництва–= 890 – 820 = 70 і нульовими елементами матриці вартості. Запишемо цю ТЗ у вигляді таблиці 1:

в a	190	200	250	250
240	9	11	16 70	15 ө 170
280	5	7 ө 200	13	10 80
300	4 190	17	12 110
70	0	0	0 70	0

Опорний план перевезень визначаємо за методом мінімальності вартості. Запишемо його у правому нижньому кутку базисних клітин. Базис складають вектори: (1;3), (1;4), (2;2), (2;4), (3;1), (3;3), (4;3).

Він є невиродженим, тому що кількість векторів базиса дорівнює: . Для визначення оптимальності плану скористаємося методом потенціалів.

Система для визначення потенціалів має вигляд:

Задаючи , отримаємо розв’язок системи:

Оцінка векторів:

>0.

Так як >0, то даний опорний план є не оптимальним.

У базис вводимо вектор (1;2). Невідомий об’єм перевезень маршруту (1;2) позначимо Θ.

Складаємо компенсаторний ланцюг. Знаходимо Θ = min (170; 200) = 170. Нова таблиця, яка відповідає новому опорному розв’язку, має вигляд:

в a	190	200	250	250
240	9	11 170	16 70	15
280	5	7 30	13	10 250
300	4 190	17	12 110	14
70	0	0	0 70	0

Базис складають вектори:

(1; 2), (1; 3), (2; 2), (2; 4), (3; 1), (3; 3), (4; 3).

Система для визначення потенціалів має вигляд:

Розв’язок цієї системи має вигляд:

Оцінки небазисних векторів:

Усі оцінки недодатні. Даний опорний розв’язок є оптимальний.

Оптимальне значення функції мети:

Відповідь: оптимальне значення функції мети при оптимальному плані перевезень:При цьому III споживач не отримає 70 одиниць продукції.

Задачі для самостійної роботи.

Розв’язати ТЗ методом потенціалів:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

Тема. Метод множників Лагранжа до задач нелінійного програмування (знп), система умов якого включає й обмеження нерівності.

Алгоритм розв’язку задачі:

1 крок. Розглядаємо всі обмеження як строгі рівності, знаходимо точки екстремуму і обчислюємо в них значення функції мети. Функція Лагранжа при цьому:

ƒ(1)

Таким чином знаходимо екстремальні точки множини планів задачі, де всі додаткові змінні дорівнюють 0.

2 крок. Відкидаємо в (1) один доданок, який відповідає одному обмеженню-нерівності і знаходимо стаціонарні точки нової задачі 2. Відбираємо серед них ті, які задовольняють відкинуте обмеження, як строгу нерівність, і знаходимо значення функції мети. Цей крок повторюємо послідовно для всіх обмежень-нерівностей.

3 крок. Відкидаємо послідовно по 2 доданка функції Лагранжа (1), які відповідають обмеженням-нерівностям і щоразу визначаємо стаціонарні точки L. Відбираємо ті стаціонарні точки, які задовольняють два відкинуті обмеження. Продовжуємо цей процес для 3 і більше нерівностей.

Глобальний екстремум потрібного типу знаходимо, порівнюючи всі обчислені значення функції мети.

Приклад 1:

1 крок.

Система рівнянь (3)–(5) несумісна і, отже не визначає жодної точки.

2 крок. Відкинемо останнє обмеження-нерівність (5) і розв’яжемо задачу Лагранжа (1– 4) при .причомузадовольняє відкинуте обмеження>2.

Відкинемо друге обмеження – нерівність (4) і розв’яжемо (1)–(3), (5) при Дістанемо:Причомузадовольняє відкинуту нерівність.

3 крок. Відкидаємо обидва обмеження-нерівності і розв’язуємо (1) – (3) при . Дістанемо:Причомузадовольняє обидві відкинуті нерівності:

Порівнюючи дістанемопри плані, тобто

Відповідь: при плані.

Приклад 2:

Узагальненим методом множників Лагранжа знайти мінімум функції для системи обмежень

Розв‘язання:

1. Записуємо функцію Лагранжа при наявності всіх обмежень:

Шукаємо стаціонарні точки функції або

Із рівняння (3) маємо

Підставимо цей вираз у рівняння (4).

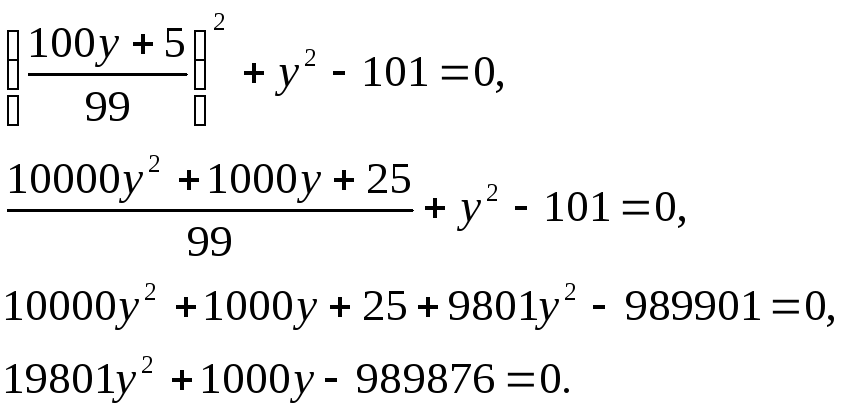
Із (5): Із (4):деТоді (1) і (2) приймають вигляд:

Маємо систему двох лінійних рівнянь відносно невідомих Помножимо рівняння (8) наа рівняння (9) – наотримаємо:

Від першого рівняння системи віднімемо друге, отримаємо

Так як (див. (6) і (7) при, тоТоді із першого рівняння останньої системи примаємо:

Так як (див. (7)), тоТодітому щозадовольняють (4). Таким чином у стаціонарних точках:

і

маємо локальні екстремуми

2. Відкидаємо обмеження-нерівність і запишемо функцію Лагранжа для випадку наявності тільки обмеження рівності:

Знаходимо стаціонарні точки функції

або

Помножимо перше рівняння системи на 100, а друге – на 99:

До першого рівняння додамо друге, отримаємо систему відносно

Зважаючи, що маємо:

Із другого рівняння системи (10):

Стаціонарна точка

Перевіряємо виконання відкинутої нерівності.

Локальний екстремум

Вибираємо

Відповідь: у точках