4.4 Метод релаксації

Нехай маємо СЛАР (4.1). Перенесемо вільні члени (4.1) наліво і розділимо: І рівняння ІІ рівняннятощо. Тоді отримаємо систему, яка підготовлена до застосування метода релаксації:

де (4.14)

Нехай - початкове наближення (4.14). Підставивши ці значення в (4.14), отримаємо нев’язки.

Якщо дати прирістто відповідна нев’язказменшиться наа всі інші нев’язкизбільшаться на величинуЩоб обернути в нуль чергову нев’язкутреба величинідати прирістТоді,а при

Метод релаксації (встановлення, ослаблення) у простішій формі полягає в тому, що на кожній ітерації зануляють чергову максимальну по модулю нев’язку шляхом зміни значення відповідної компоненти наближення. Процес закінчується, коли усі нев’язки останньої перетвореної системи будуть дорівнювати 0 із заданою точністю.

Приклад. Методом релаксації розв’язати систему, обчислюючи з точністю до

(4.15)

Запишемо (4.15) у вигляді, придатному для релаксації (4.16). У зведеному вигляді маємо:

(4.16)

Виберемо початкове наближення і знайдемо відповідні нев’язкиТоді дляk+1- го наближення отримаємо:

(4.17)

За загальною теорією вибираємо ТодіАналогічно попередньомутощо. Результати обчислень наведені в таблиці 4.2

Результати обчислень Таблиця 4.2

	0	0	0	0,93	0	0	0,07	0	0	1,00
	0,60	0,76	0,93	0	0,04	0,07	0	0	0
	0	0	0,86	0	0	0,13	0	0	0,01	1,00
	0,70	0,86	0	0,09	0,13	0	0,01	0,01	0
	0	0,8	0	0	0,18	0	0	0,02	0	1,00
	0,80	0	0,09	0,18	0	0,01	0,02	0	0

Відповідь: .

4.5 Метод прогонки

Метод застосовується для розв’язування СЛАР, основна матриця яких має трьох-діагональний вигляд:

(4.18)

Розширена матриця системи (4.18)

Перше і останнє рівняння системи (1) містять по 2 невідомих. Їх можна розглядати як крайові умови.

Необхідно знайти розв’язок системи (4.18) методом виключення Гауса.

Якщо до (4.18) застосувати етап прямого хода Гауса, то замість отримаємо, яка має три діагональний вигляд:

.

Звідси формула зворотного ходу:

(4.19)

Формула для коефіцієнтів прогонки івизначаються, якщо записати (4.19) дляі підставити в (4.18):

(4.20)

Це формули прямого ходу.

Зворотний хід метода прогонки починається з обчислення , для чого використовуються останні рівняння (4.19) і (4.18) ,. Звідки

(4.21)

Інші значення невідомих визначаються по (4.19).

4.6 Методика розв’язування задачі

Прямий хід.

1. Обчислюються .

2. Обчислюють коефіцієнти прогонки за формулами (4.20).

Зворотний хід.

3. Визначається

4. За формулами (4.19) знаходять

Зауваження

1. Даний метод називається методом скалярної прогонки, тому що при розв’язуванні задачі на кожному і-му кроці визначається скалярна величина

2. Аналогічний підхід використовується для розв’язування СЛАР з п’яти-діагональними матрицями.

3. Алгоритм методу прогонки коректний, якщо для всіх маємоістійкий, якщо .

4. Достатньою умовою коректності і стійкості прогонки є умова переваги діагональних елементів в матриці для:

(4.22)

і має строгу нерівність хоча б при одному і.

5. Алгоритм методу прогонки є досить економічним і потребує для своєї реалізації кількість операцій пропорційно п.

Приклад 1. Розв’язати СЛАР методом прогонки

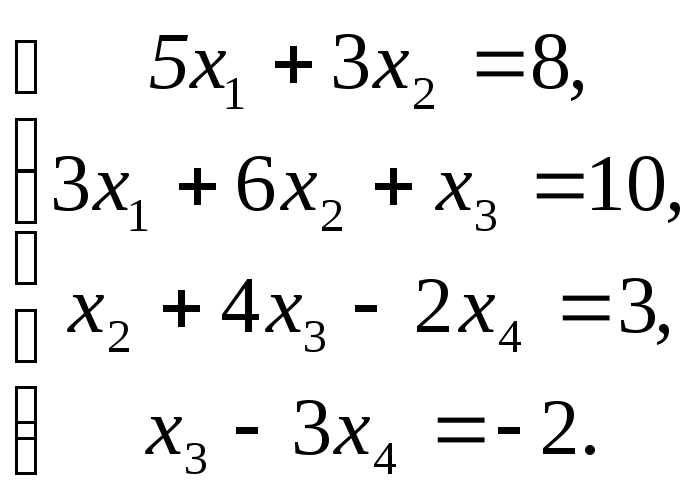
Дана система задовольняє умові коректності і стійкості прогонки, бо

Розширена матриця системи .

Прямий хід. Обчислимо коефіцієнти прогонки.

Зворотний хід:

Відповідь:

Приклад 2. Розв’язати СЛАР методом прогонки

СЛАР не задовольняє умовам коректності і стійкості прогонки.

Прямий хід.

Зворотний хід.

Відповідь: