5.13 Метод найкращого інтегрального наближення

Глобальний спосіб. Шукаємо коефіцієнти згладжуючого многочлена

(5.19)

із умови:

, (5.20)

якщо функція задана на кожному частинному відрізку інтеграломі з умови:

(5.21)

якщо функція задана на кожному частинному відрізку з фіксованим лівим вузлом

Інтегруючи ліві частини (5.20) або (5.21) після підстановки (5.19) отримаємо СЛАР з невідомими коефіцієнтами. Розв’язавши її отримаємоі, відповідно,.

Зауваження.

1. Системи (5.20) і (5.21) рівносильні і отримуються одна з одної за допомогою лінійних комбінацій (додаванням або відніманням рівнянь).

2. Системи (5.20) і (5.21) мають єдиний розв’язок, тому що визначники основних матриць цих СЛАР відмінні від 0. Таким чином, задача знаходження многочлена найкращого інтегрального наближення (5.19) має єдиний розв’язок.

3. При великих т глобальний спосіб побудови многочленів найкращого інтегрального наближення, як і інтерполяційних многочленів, використовувати не рекомендується.

Кусковий спосіб. Нехай сіткова функція задана на деякій сітковій області і многочлен степенят, який наближає функцію , будується на деякому внутрішньому відрізку, який у свою чергу міститьчастинних відрізків, на яких задані інтеграли. За цими означеннями інтегралів будується будь-яким способомна вказаному відрізку (наприклад, за допомогою скінченно-інтегральних різниць дот-го порядку включно для величини .

5.14 Методи інтерполяції та згладжування на основі сплайнів

Як відмічалося вище, при глобальному способі апроксимації високі степені інтерполяційних многочленів використовувати недоцільно. Тому часто застосовують кусково-глобальний метод інтерполяції. Але похідні таких інтерполяційних многочленів, які утворюються на частинних відрізках, розривні на межі відрізків. У ряді випадків це призводить до небажаних наслідків [2].

Таким чином, разом з функцією , необхідно досить добре апроксимувати і її похідні. Це зумовлює необхідність побудови сплайн-функцій, які мають вказані властивості і мають інтерполюючий або згладжуючий характер.

Нехай на відрізку задана сіткова функціяна сітці. Треба побудувати функцію, дет – степінь многочлена, кусково-глобальним способом.

Сплайн-функція (сплайн) – сукупність - алгебраїчних многочленів степенят, які визначені на частинних відрізках і об’єднаних разом по всім частинним відрізкам так, щоб можливо було скласти багатоланкову функцію, яка визначена і неперервна на всьому відрізкуразом зі всіма своїми похіднимидо деякого порядку

Різниця між т – степенем многочлена і найбільшим порядком похідної р, яка є неперервною на відрізку , визначаєдефект сплайна .

Умови узгодженості ланок сплайна з вихідною функцієюна відповідному частинному відрізку- умови, які накладаються на нев’язки диференціального або інтегрального типів, і які використовуються для отримання формул однієї ланки на вказаному частинному відрізку.

Сплайн, який задовольняє умовам нульових функціональних нев’язок: , називаєтьсяінтерполяційним, а який задовольняє тільки інтегральним умовам -згладжуючим або інтегрально-згладжуючим.

Диференціальний (D-сплайн) – сплайн, який задовольняє диференціальним умовам узгодженості:

при або.

Інтегрально-диференціальний (ІD) сплайн – якщо разом з диференціальними умовами використовуються і інтегральні умови.

Кількість умов узгодженості, які необхідні для отримання формул однієї ланки сплайна, повинна відповідати степеню сплайна (кількість умов на одиницю більше т).

При розв’язуванні задачі апроксимації за допомогою сплайн-функцій умови стиковки перетворюється до співвідношень між параметрами сплайна, які називаються параметричними співвідношеннями.

Локальний сплайн – якщо всі невизначені параметри, які відносяться до кожної ланки , привизначаються локально, тобто незалежно від параметрів, які характеризують усі інші (або майже всі інші) ланкипри, тобто.

Таким чином, сплайн-апроксимація (як правило, це інтерполяція) локальними сплайнами зводиться до обчислення коефіцієнтів многочленів для кожної ланки результатного сплайна. Недолік локальної апроксимації полягає в тому, що таким способом не вдається забезпечити мінімальний дефект сплайна, тобто максимальну його гладкість – неперервність похідних якомога більшого порядку.

Глобальний сплайн – для якого невизначені параметри, які відносяться до кожної ланки, знаходяться сумісно з параметрами, які характеризують всі інші ланки. Невизначені параметри в глобальних сплайнах для всіх ланок обчислюються, як правило, розв’язуванням СЛАР трьохдіагонального вигляду методом прогонки, причому це забезпечує мінімально можливий дефект сплайнів. Тому глобальні сплайни широко використовуються в обчислювальній математичці.

Розгорнуте визначення глобального інтегрально-диференціального сплайна.

Функція , яка визначена на відрізку, належить до класу гладкостіі складена із сукупності ланок, які визначені на кожному частинному відрізкусітки, називаєтьсяалгебраїчним інтегрально-диференціальним сплайном степеня т і дефекта з вузлами на сітці, якщо кожна його ланкапредставляється у вигляді алгебраїчного многочлена степенят: з коефіцієнтами, які визначаються із сукупностіінтегральних або диференціальних умов узгодження

, (5.22)

, (5.23)

та із умов неперервності ланок по похідним

, (5.24)

де причому.

Зауваження:

1. Визначення узагальнене і стосується як інтегрально-диференціального сплайна, так і класичного диференціального (для нього (5.22) не використовується).

2. Умова неперервності (5.24) разом із (5.23) забезпечує неперервність 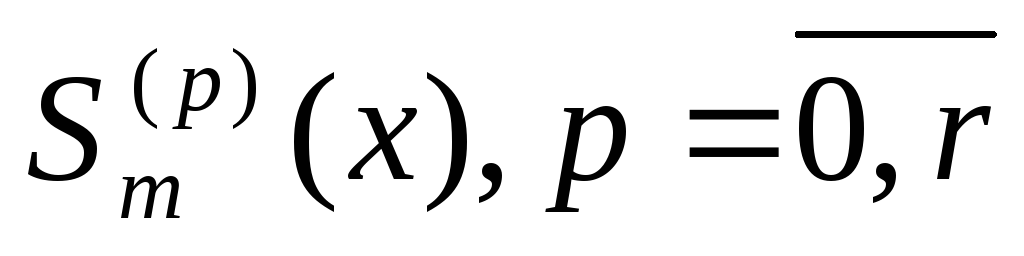у всіх внутрішніх вузлах, які визначають точки дотику ланок. Це гарантує виконання умови.

3. Алгоритм побудови сплайна включає в себе два способи апроксимації – кусковий і глобальний.

4. Порядки похідних р в умовах (5.23) не повинні збігатися з порядками похідних в умовах (5.24), але сукупність порядків похідних повинна забезпечити виконання умови.

5. Найбільш поширеними є кубічні диференціальні сплайни.