, , .

Практичнее заняття №6.

Нормальний закон розподілу

Означення. НВВ розподілена за нормальним законом з параметрамита, якщо її щільність розподілу імовірностей має вигляд:

.

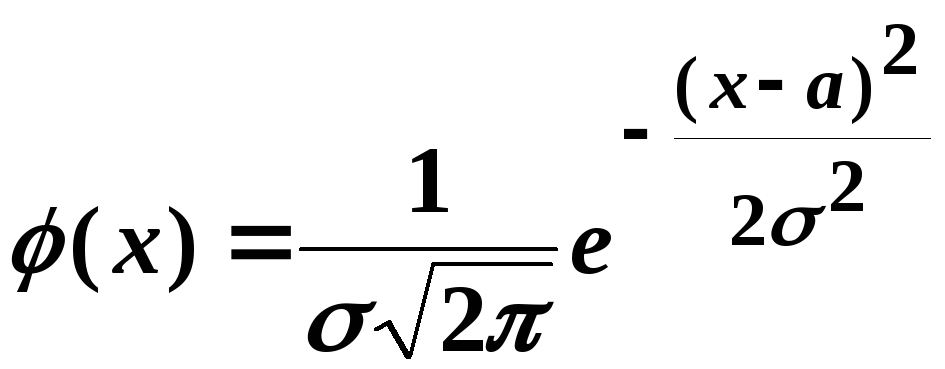Скористувавшись означеннями, неважко переконатись, що числові характеристики нормально розподіленої ВВ дорівнюють:

.

інтегральна функція Лапласа , остаточно дістаємо:

.

ДЕЯКІ ВЛАСТИВОСТІ НОРМАЛЬНОГО РОЗПОДІЛУ.

1. Імовірність попадання значень нормально розподіленої ВВ до проміжку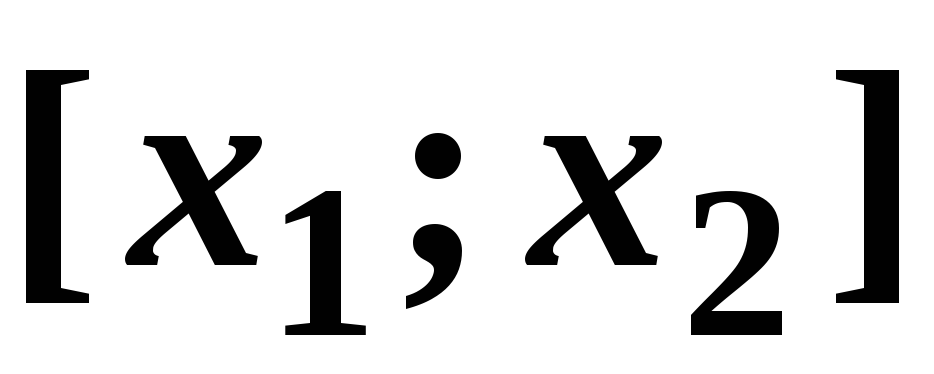знаходиться за формулою:

2.Імовірність того, що модуль відхилення нормально розподіленої ВВ від свого математичного сподівання не перевищить величину, дорівнює

. .

3.Правило трьох сигм. Із практичною достовірністю (з імовірністю 0,9973) можна стверджувати, що значення нормально розподіленої ВВ попадають до проміжка.

Практичне заняття №7.

Означення. Біноміальным законом розподілу ДВВ називають ДВВ - частоту появи подіїуНПВ, таблиця розподілу якої має наступний вигляд:

			…
			…

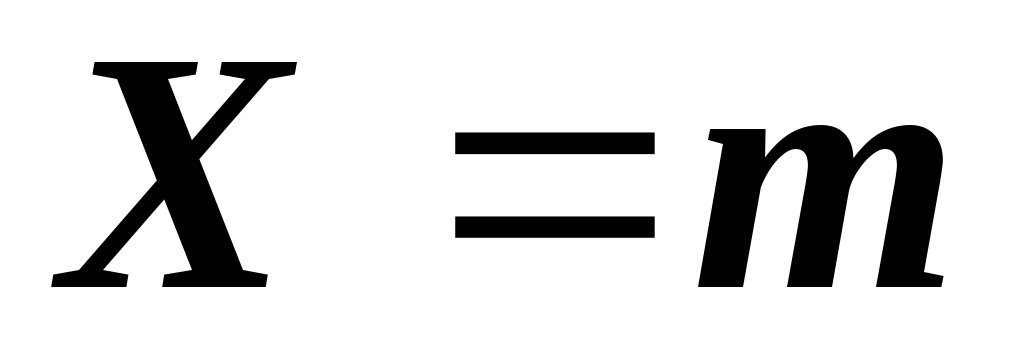
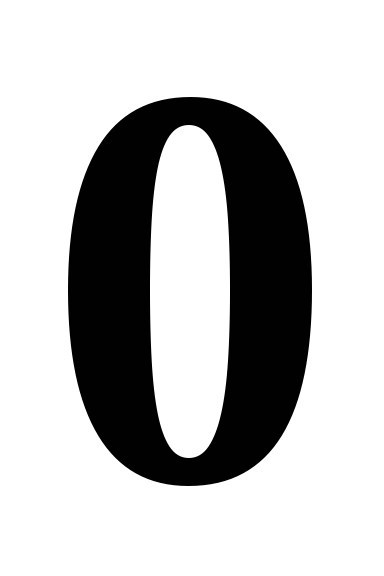
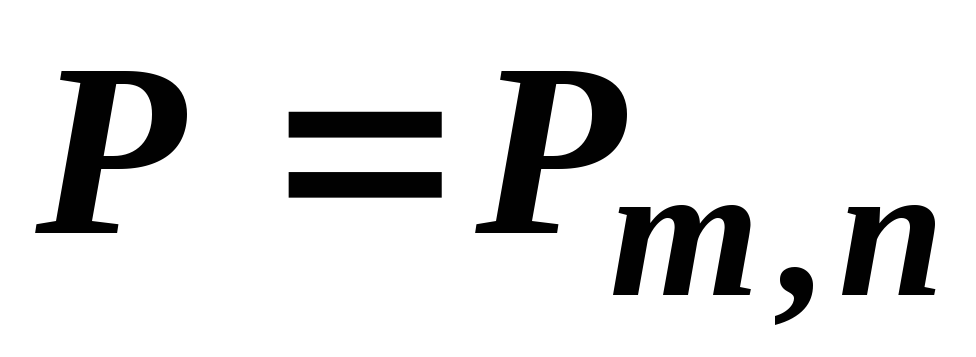
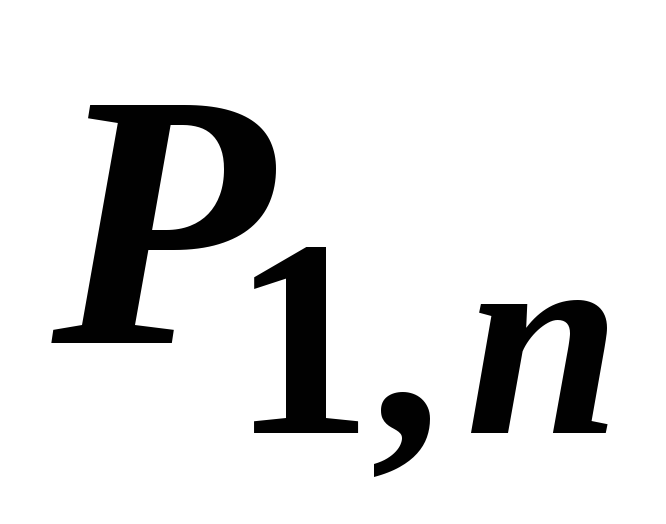
Відзначимо, що . Це випливає із формули бінома Ньютона та очевидної рівності:

Інтегральна теорема Муавра-Лапласа. Для біноміально розподіленої ДВВ - частоти появи подіїз імовірністюв серії ізНПВ справедлива наближена формула:

,

де - інтегральна функція Лапласа, .

Частинні випадки інтегральної теореми Муавра-Лапласа . Для частоти та частості появи події з імовірністюв серії ізНПВ справедливі наближені формули:

,

.

Практичне заняття №8.

Теорема (нерівність Маркова). Якщо ВВ приймає тільки невід’ємні значення і має фіксоване математичне сподівання, то для довільного додатного числасправедлива нерівність:

.

Наслідок (друга форма нерівності Маркова) . За умовами теореми

.

Теорема (нерівність Чебишова). Якщо довільна ВВ має фіксовані математичне сподіваннята дисперсію, то для довільного додатного числасправедлива нерівність:

.

Наслідок (друга форма нерівності Чебишова) . За умовами теореми

.

Теорема Чебишова. Якщо всі дисперсії послідовності попарно незалежних ВВ не перевищують деякого додатного числа, то примайже достовірним можна вважати подію, яка полягає у тому, що модуль відхилення середнього арифметичного ВВ від середнього арифметичного їх математичних сподівань буде величиною нескінченно малою, тобто:

.

Теорема Бернуллі. Частість появи подіїв серії ізНПВ призбігається за імовірністю до- імовірності появи події у кожному окремому випробуванні:

, або .

Якщо всі дисперсії послідовності попарно незалежних ВВ не перевищують деякого додатного числа, то примайже достовірним можна вважати подію, яка полягає у тому, що модуль відхилення середнього арифметичного ВВ від середнього арифметичного їх математичних сподівань буде величиною нескінченно малою, тобто:

.