4.3. Понятие изоморфизма и изоморфизм плоских графов

Один и тот же граф можно изображать по разному.

Во‑первых, в соответствии с описанием графа, вер­ши­ны допускается представлять точками, которые в про­стран­ственном отношении могут располагаться произ­вольно друг по отношению к другу, но так чтобы разным вершинам отвечали бы и разные точки. Очевидно, что, в этом случае, несмотря на то, что визуальное изображение графа может существенно измениться, оба изображения — исходное и измененное — должны соответствовать одному и тому же описанию графа.

Во‑вторых можно перенумеровать вершины уже изо­бра­женного графа и при этом потребовать не различать описа­ний, поскольку граф при этом фактически остался тем же.

В таких ситуациях необходимо четко определиться ка­кие графы различаются, а какие — нет. С этой целью вводится понятие изоморфизма графов. Слово «изо­морфизм» в переводе с греческого означает — одинаковой формы.

Графы G(V,U) и G (V, U) называются изоморфными, если существует биекция между множествами вершин V и V, а также между множествами ребер U и U, сохраняющая отношение инцидентности: если v  V, v  V, u  U и u  U, то вершина v инцидентна ребру U тогда и только тогда, когда вершина v инцидентна ребру U.

Графы, содержащие различное число вершин или ребер, не могут быть изоморфными.

Понятие изоморфизма позволяет упростить решение ряда задач. Поясним это на примере решения задачи укладки графов. Под укладкой графа понимают такое его изоморфное преобразование, при котором граф становится плоским.

Задача укладки имеет применение, например, при разработках информационных, транспортных, энергетических сетей, и т.д.

Одной из первых задач укладки графов была следующая старинная шуточная задача. Три поссорившихся соседа име­ют три общих колодца. Можно ли провести непересека­ющиеся дорожки от каждого дома к каждому из колодцев?

Строгое доказательство невозможности получения положительного решения этой задачи принадлежит Жордану. Им была доказана следующая теорема, которая на первый взгляд кажется очевидной.

Теорема 4.1 (Жордан) Если L — непрерывная за­мкнутая кривая без самопересечений на плоскости (рисунок 4.5), то L делит плоскость на внешнюю и внутреннюю области так, что любая непрерывная линия, соединяющая две точки x и у с внутренней и внешней области, пересекает L.

L y

x

Рисунок 4.5

Построим для задачи о трех соседях и трех колодцах граф, соответствующий взаимному расположению домов и колодцев. Этот граф изображен на рисунке 4.6 слева

На рисунке 4.6 справа изображен граф, изоморфный исходному. Из теоремы Жордана следует, что соединение вершин v_d3 и v_k2 ребром без пересечения с замкнутой кри­вой L не представляется возможным.

v_d1 v_d2 v_d3

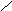.. . v_{k1 L}

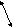
.. .v_d1 v_d3 v_d2

v_k3

v_k1 v_k2 v_k3 v_k2

Рисунок 4.6

Конечно, пытаясь получить любое другое решение задачи, можно перенумеровать вершины нашего графа, однако, поскольку перенумерация вершин любого графа с со­хранением инцидентности этих вершин ребрам приводит к изоморфизму этих же графов, то и в общем случае имеем от­рицательное решение задачи о трех колодцах и трех пос­сорившихся соседях.

Граф, изображенный на рисунке 4.6 слева, получил специальное обозначение A₃₃.

Другой, замечательный в отношении планарности граф, представлен на рисунке 4.7.

Этот граф имеет обозначение U₅₅. Обозначение U обы­чно принимается для полных графов.

То, что граф U₅₅ не плоский, доказывается точно так­же, как и для графа A₃₃.

В теории плоских графов один из фундаментальных результатов принадлежит Понтрягину и Куратовскому. Ими доказана следующая теорема.

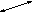
v₂ v₃

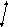v₁

v₄ v₅

Рисунок 4.7

Теорема 4.2 (Понтрягин и Куратовский) Для того, чтобы граф G был плоским, необходимо и достаточно, чтобы он не содержал частичного графа, изоморфного A₃₃ или U₅.

Доказательство этой теоремы ввиду его громоздкости мы опускаем.