1.3. Понятия образа, прообраза, функции и отображения на конечном множестве. Аксиома выделения.

Рассмотрим декартово произведение множеств A и B. Пусть на AB определено некоторое отношение R. Пусть также D_l и D_r ‑ левая и правая части этого отношения. Определим некоторое подмножество X  D_l и построим под­множество Y  Dr, как множество всех тех вторых эле­ментов пар x, y  R, для которых x  X. Множество Y называют образом множества X при отношении R.

Для образа применяют специальное обозначение: R¹(X). В нашей постановке R¹(X) = Y.

Пусть Y  D_r. Определим подмножество X^c  D_l, как мно­жество всех тех первых элементов пар x, y  R, для ко­торых y  Y. Множество X^c называют прообразом множества Y при отношении R. Прообраз обозначают: R^-1(Y).

На рисунке 1.5 представлено отношение R, отмеченное символом «», на декартовом произведении множеств A = = {1, 2, 3, 4, 5} и B = {1, 2, 3, 4}.

Полагая, например, X = {2, 3} A, получим R¹(X) = = {3, 4} = Y. С другой стороны, полагая Y = {3, 4}, получим X^c = =R^-1(Y) = {1, 2, 3, 4}. Из этого примера видно, что X, в общем случае, не равно X^c, то есть R^-1(Y)  X.

Отношение R  X  Y называется функцией, если для любых x  X и y₁, y₂  Y таких, что (x, y₁)  R и (x, y₂)  R следует, что y₁ = y₂.

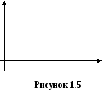B

4      

3      

2      

1      

    

1 2 3 4 5 A

Из этого определения, в частности, следует, что отношение R, представленное рисунком 1.5, функцией не является. Примером функции на том же декартовом произ­ведении является отношение R, представленное на рисунке 1.6

B

4      

3      

2      

1      

    

1 2 3 4 5 A

Функции обычно обозначают малыми латинскими буквами f, g, h … . Левая D_l(f) и правая D_r(f) области отношения f называются, соответственно областью определения и областью значений функции f.

На рисунке 1.6 областью определения отношения f является множество D_l(f) = {1, 2, 3, 4}, а областью значений — множество D_r(f) = {2, 3, 4}.

Применяется и другая терминология. Если D_l(f) = X, а D_r(f)  Y, то f называют отображением множества X в мно­жество Y. Если же при этом D_r(f) = Y, то f называют отображением мно­жества X на множество Y или сюръекцией.

Если D_l(f) = X, то говорят, что f определена на X. Множество всех отображений из X в Y обозначают си­м­во­лами «Y^X». Утверждение f  Y^X принято записывать также в виде: F: X  Y.

Из определения функции вытекает, что существует не более одного элемента y  Y, такого, что xfy. То есть эле­мент y определяется функцией однозначно. Его называют значением функции f для аргумента x и обозначают f(x).

Пусть D_l(f) — область определения и D_r(f) — область значений функции f. Если для любых двух различных x₁ и x₂ значения функции f(x₁) и f(x₂) также различны, то такая фу­нкция называется инъективной.

Функция f называется биективной или взаимно‑одно­значной функцией, если она сюръективна и инъективна.

Для взаимно‑однозначных функций имеет место следующая теорема.

Теорема 1.6 Если функции f и g взаимно‑одно­значны, то функция f(g(x)) также взаимно‑одно­значна.

Доказательство. Действительно, f(g(x)) = f(g(x)), тогда и только тогда, когда g(x) = g(x) и, соответственно, g(x)= = g(x) тогда и только тогда, когда x = x, что и требовалось.

Поясним введенные определения геометрическими построениями. На рисунке 1.7 представлена функция f общего вида. Ее значения отмечены символом «». Из рисунка видно, что областью ее определения является множество X = ={1, 2, 3, 4, 5}, а областью значений — множество Y = ={2, 3, 4}.

B

4      

3      

2      

1      

    

1 2 3 4 5 A

Пример сюръективной, но не инъективной функции, представлен на рисунке 1.8. Эта функция инъективной не является, поскольку элементы 3 и 5 множества X принимают одни и те же значения на множестве Y.

B

4      

3      

2      

1      

    

1 2 3 4 5 A

Очевидно, что биекцию можно построить на декартовом ква­драте. Функция f, изображенная на рисунке 1.9 дает пример та­кого (и далеко не единственного) построения. Далее можно заметить, что биекция не нарушится, если заменить каждый элемент образа на пропорциональный ему элемент. Из определения биекции вытекает, что мно­жества образа и прообраза должны содержать равное число элементов: для каждого значения аргумента имеем единственное значение функции и обратно. Эта точка зрения будет значительно расширена в после­дующих параграфах при изучении бесконечных множеств.

B

4     

3     

2     

1     

    

1 2 3 4 A

Рисунок 1.9

В заключение этого параграфа отметим, что понятие функции позволяет заменить аксиому пары более общей аксиомой — аксиомой выделения (Z5).

Аксиома выделения (Z5). Пусть X — про­из­воль­ное множество, x  X и (x) — функция со значениями на множестве {0, 1}. Тогда существует множество Z, для которого x  Z тогда и только тогда, когда x  X и (x) = 1.

Функции, которые могут принимать любое одно из двух значений: {0, 1} — называются бинарными. В алгебре ло­гики бинарные функции рассматриваются как выска­зыва­тельные функции или предикаты. В таком случае их значе­ния интерпретируются соответственно как «ложь» или «ис­тина».

Рассмотрим пример. Пусть X  Y — декартово произведение 4  4 элементов и x, y  X  Y. Определим z), (z = x, y) следующим образом. Скажем, что

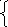1, если x = y,

z) =

0 в противном случае.

Перебирая все элементы декартового произведения, получим множество Z, как подмножество X  Y, определяющее значение единица высказывательной функции (z). В нашем примере получим Z = {1, 1, 2, 2, 3, 3, 4, 4}. Оно представляет линейную биекцию из X на Y.

Итак, аксиома выделения дает нам метод построения множеств. В частности, становится ясно, что аксиома пары есть весьма частный случай аксиомы выделения. Однако, между ними столь велико число логических построений, что применение аксиомы пары в системе аксиом теории множеств методологически вполне оправдано.