4.9. Гамильтоновы циклы. Оценка временной сложности алгоритмов

Цикл на графе G называется гамильтоновым, если соответствующая ему последовательность ребер содержит каждую вершину графа G в точности один раз.

Аналогично вводится понятие гамильтонова контура на ориентированном графе.

Примеры гамильтонового цикла и графа, для которого такого цикла не существует представлены на рисунке 4.12.

а) v₁ б) v₁

v₂ v₄ v₅ v₂ v₄ v₅

v₃

v₃

Рисунок 4.12

На рисунке 4.12 а) направление одного из гамильтоновых циклов отмечено стрелками. Соответствующий гамиль­тонов цикл представлен последовательностью ребер {(v₁, v₄), ( v₄, v₅), (v₅, v₃), (v₃, v₂), (v₂, v₁)}. Можно заметить, что ребро (v₄, v₃) в этом цикле не используется. Этот факт ука­зывает на то, что в гамильтоновом цикле могут участвовать не все ребра графа. Существенным в цикле данного типа яв­ляется наличие всех вершин графа. В связи с этим, в слу­чаях, когда нет кратных ребер, гамильтонов цикл запи­сывают последовательностью вершин. Так в рассмотренном примере гамильтонов цикл можно представить следующей последовательностью вершин: [v₁, v₄, v₅, v₃, v₂]. Нетрудно заметить, что при такой записи каждый гамильтонов цикл должен соответствовать некоторой допустимой перестановке всех вершин графа. Ясно, что одному и тому же графу мо­жно поставить в соответствие некоторое множество гамильтоновых циклов. Пример на рисунке 4.12 б) иллюстрирует случай, когда это множество пусто, поскольку вершина v₄ необходимо должна быть повторена дважды.

Укажем некоторые задачи, интерпретация которых сос­тоит в необходимости построения гамильтоновых циклов.

Задача о шахматном коне. Можно ли начиная с про­извольного поля на шахматной доске ходить конем в та­кой последовательности, чтобы пройти через все поля и вер­нуться в исходное?

Задача о званом обеде. Обед накрыт на круглом столе. Среди приглашенных некоторые являются друзьями. При каких условиях можно рассадить всех так, чтобы по обе стороны от каждого из присутствующих сидели его друзья?

Задача о коммивояжере. Коммивояжер должен объездить все n городов. Для того, чтобы сократить свои расходы он хочет построить такой маршрут, чтобы объездить все го­рода точно по одному разу и вернуться в исходный с мини­мумом затрат.

В настоящее время не по­лучено необходимых и достаточных условий суще­ств­ова­ния для гамильтоновых циклов.

С другой стороны, существует очевидный алгоритм, который казалось бы можно применить к решению любой за­дачи о гамильтоновом цикле: генерируем все перестановки вершин и проверяем, какая из них является гамиль­то­но­вым циклом. Всех перестановок, очевидно, будет n!

Оценим временную сложность этого алгоритма. Она вводится аналогично рассмотренной в 4.6. Под временной характеристикой сложности алгоритма понимают асимптотическую оценку О(f(n₁, n₂, …n_k)) требуемого вре­мени работы компьютера в зависимости от мощностей n₁, n₂, …, n_k множеств исходных данных при неограниченном уве­личении этих мощностей. Поскольку компьютеры могут об­ладать различной производительностью, то оценка времен­ных затрат может быть выражена в количестве эле­мен­тар­ных операций: сложений, умножений или других опе­раций, выполняемых компьютером и принятых за основу.

Легко видеть, что ограничением применения предложенного выше метода является то, что для его реализации потребуется О(nn!) вычислительных операций (n операций на каждую из n! перестановок). Так, если n = 20 и каждый элементарный шаг компьютера выполняется за 10^-7 с, то ре­шение задачи о построении гамильтонова цикла займет по­рядка 20*20!48*10¹⁸ операций или 45*10¹¹ с, что сос­та­вляет порядка 1500 веков.

Проблема существования гамильтонового цикла принадлежит к классу так называемых NP‑полных задач. Это широкий класс задач, для которых не известен алгоритм по­линомиальной сложности их решения, то есть алгоритм с числом шагов, ограниченных полиномом от размерности за­дачи. Задача же построения гамильтонового цикла, как ука­зано выше, в максимальном случае решается алгоритмом факториальной сложности.

Для того, чтобы убедиться в том, что значения nn! растут быст­рее, чем значения произвольного многочлена, покажем, что они растут быстрее, чем значения показательной функции, начиная с неко­торого достаточно большого значения n.

Для этого рассмотрим варианту

x_n = cⁿ / nn!, с > 1.

Нетрудно заметить, что

x_n+1 = x_nc / (n + 1).

Поэтому, как только n + 1 > c эта варианта становится убывающей, а поскольку она ограничена нулем, то предел ее также есть нуль.

Для решения NP‑полных задач известен метод, позво­ляющий сократить число шагов, сводя задачу от факто­ри­альной к экспоненциальной сложности. Этот метод извес­тен под названием «backtracing» или «алгоритм с воз­вратами». Его суть в применении к задаче построения га­миль­тоновых циклов состоит в следующем.

Будем искать решение в виде последовательности вер­шин v₁, v₂, …, v_n, начиная от корневой вершины v₁. Имея частичное решение v₁, v₂,…, v_i, i < n, пытаемся найти та­кое допустимое значение v_{i + 1,} относительно ко­то­ро­­го можно предположить, что оно может расширить частичное решение до v₁, v₂,…, v_{i + 1}. Если такое предположение возможно, то v_{i + 1} включается в частичное решение и процесс продолжается. Если никакая вершина не может пре­тен­довать на v_{i + 1}, то следует возврат на шаг к v_{i - 1}, а v_i из дан­ного частичного решения исключается. Процесс поиска но­вого допустимого значения продолжается, начиная с v_{i - 1}. Когда v_n найдено, отмечают v₁, v₂, …, v_n  как решение.

Если поставлена задача отыскания всех решений, то попытка получения каждого нового решения осуществляется возвратом на шаг от v_n в предположении, что решение как бы получено не было. Таким образом, отыскивается мно­жество всех решений, которое, в частности, оказывается пу­стым, если гамильтонова цикла на графе не существует.

Из описания алгоритма с возвратами видно, что задача построения всех гамильтоновых циклов на графе G может быть решена путем сопоставления исходному графу неко­торого другого графа G, построенного из частично пересе­кающихся цепей v₁, v₂, …, v_i, (i  n). Подмножество G, состоящее из цепей v₁, v₂, …, v_n, таких что v_n смежна с v₁ на G представляет множество решений задачи. Граф G называется соотнесенным графом.

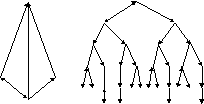
Рассмотрим решение задачи о коммивояжере на примере графа G, представленного на рисунке 4.13. Имеем пять пунктов V = {1, 2, 3, 4, 5}. Стоимость доставки информации из пункта i в пункт j представлена числами над ребрами графа. Требуется, используя компьютерную сеть, моделируемую данным графом, обеспечить перекличку пунктов (например, фирм, принадлежащих одной корпорации и т.д.), начиная из пункта 1. Для решения поставленной задачи построим гамильтонов цикл минимальной стоимости передачи информации, либо несколько таких циклов в случае их одинаковой стоимости.

Задачу будем решать в два этапа. Вначале построим все гамильтоновы циклы из пункта 1. Для этого применим алго­ритм с возвратами. Затем на множестве полученных ци­клов выберем циклы минимальной длины.

Построение цепей графа G применением алгоритма с возвратами поясняется рисунком 4.13 справа. На этом рисунке цепи, соответствующие гамильтоновым циклам, выделены жи­рными линиями.

Всего имеем четыре гамильтоновых цикла:

1. {1, 2, 3, 5, 4, 1}

2. {1, 2, 5, 3, 4, 1},

3. {1, 4, 3, 5, 2, 1},

4. {1, 4, 5, 3, 2, 1}.

Стоимости передачи информации каждым из этих циклов вычисляются ниже:

1. 9+10+2+2+6 = 29,

2. 9+8+2+5+6 = 30,

3. 6+5+2+8+9 = 30,

4. 6+2+2+10+9 = 29.

Решению поставленной задачи отвечают гамильтоновы циклы a) и d).

Можно показать, что алгоритмы с возвратами имеют вычислительную сложность О(сⁿ), где c > 1 — константа, оп­ределяемая свойствами присоединенного графа. Такое бы­стродействие при больших n значительно выше, чем в слу­чае применения алгоритмов факториальной сложности. На­пример, возвращаясь к рассмотренному выше примеру оцен­ки быстродействия алгоритма с возвратами при n = 20 видим, что в случае, когда с = 2 (граф G двоичное дерево)

G G

2 1

(9) (10) 2 4

3 5 3 5

(8)

4 5 3 4 2 5 2 3

1 5 (2 ) 3

(2) 1 5 4 4 1 3 1 5 2 1 3 2

(6) (5)

4 1 1 1 1

Рисунок 4.13

имеем всего 2²⁰ или порядка 10⁶ вычислительных операций. На любом современном компьютере это практически не займет времени. Однако, при увеличении размерности задачи всего лишь в несколько раз снова возникают про­блемы реального времени. Это способствует развитию но­вых идей построения гамильтоновых циклов.