
- •§1. Первообразная и неопределенный интеграл: основные определения и теоремы
- •§2. Таблица основных интегралов
- •§3. Основные правила интегрирования
- •§4. Основные методы интегрирования
- •I Непосредственное интегрирование
- •II Метод замены переменной
- •II.1 Подведение под знак дифференциала
- •II.2 Метод подстановки
- •III Интегрирование по частям
- •§5. Интегрирование некоторых выражений, содержащих квадратный трехчлен
- •§6. Интегрирование рациональных функций
- •I Рациональные функции
- •1) ; 2); 3); 4).
- •II Интегрирование простейших дробей
- •III Интегрирование правильных рациональных дробей
- •§7. Интегрирование некоторых тригонометрических выражений
- •I Интегралы вида
- •II Интегралы вида
- •V Интегралы вида
- •III Квадратичные иррациональности: общий случай,
- •IV Интегрирование биномиальных дифференциалов:
§5. Интегрирование некоторых выражений, содержащих квадратный трехчлен
В этом параграфе рассматриваем интегралы вида
![]() ,
,
![]() .
.
В
квадратном трехчлене выделим полный
квадрат
![]() ,
где
,
где![]() ,
а
,
а![]() .
После этого интеграл можно разбить на
сумму двух интегра-
.
После этого интеграл можно разбить на
сумму двух интегра-
лов. Например,
![]()
 .
.
Интеграл
в первом слагаемом – это
![]() ,
а во втором – арктангенс или «высокий»
логарифм.
,
а во втором – арктангенс или «высокий»
логарифм.
Аналогично
для
![]() получим:
получим:
 .
.
Здесь
первый интеграл равен
![]() ,
а второй – это арксинус или «длинный»
логарифм.
,
а второй – это арксинус или «длинный»
логарифм.
Примеры.
1.
![]()
![]() .
.
2.
![]()
![]() .
.
Замечание.
Если
![]() ,
то интегралы
,
то интегралы
![]() и
и![]() после выделения полного квадрата можно
найти с помощью правилаIII
из §3 (замена переменной не обязательна).
после выделения полного квадрата можно
найти с помощью правилаIII
из §3 (замена переменной не обязательна).
§6. Интегрирование рациональных функций
I Рациональные функции
Определение. Рациональной функцией (или рациональной дробью) называется отношение двух многочленов
![]() .
.
При
этом дробь называется правильной, если
![]() ;
в противном случае дробь называется
неправильной.
;
в противном случае дробь называется
неправильной.
Из алгебры известно, что неправильную дробь путем деления числителя на знаменатель «столбиком» можно представить в виде суммы многочлена и правильной дроби. Например,

поэтому
![]() .
.
Интегрирование многочлена не представляет трудностей, поэтому надо сосредоточиться на интегрировании правильных дробей.
Среди всевозможных правильных дробей выделяют так называемые
простейшие дроби следующих четырех типов:
1) ; 2); 3); 4).
Здесь:
![]() ;
;![]() – действительные числа, причем
– действительные числа, причем![]() .
.
II Интегрирование простейших дробей
Правило III §3 позволяет сразу написать
![]() ,
,
![]() .
.
Чтобы
проинтегрировать дроби третьего и
четвертого типов, следует выделить
полный квадрат, сделать замену переменной
и разбить интеграл на сумму двух
интегралов. Например, для дроби третьего
типа
![]() :
:

![]()

Для дроби четвертого типа аналогично будем иметь
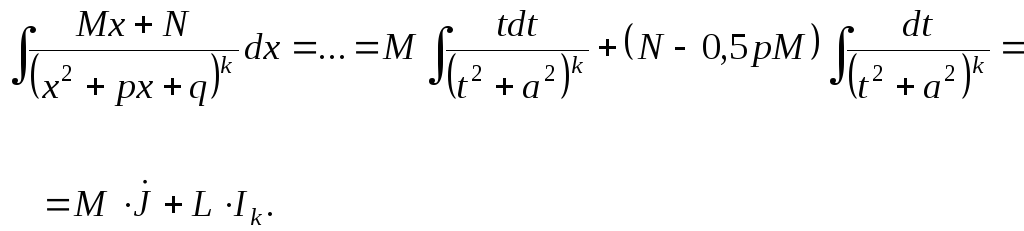
Здесь
интеграл
![]() вычисляется путем подведения под знак
дифференциала:
вычисляется путем подведения под знак
дифференциала:


Для интеграла во втором слагаемом можно вывести рекуррентную формулу, предварительно преобразовав его следующим образом:
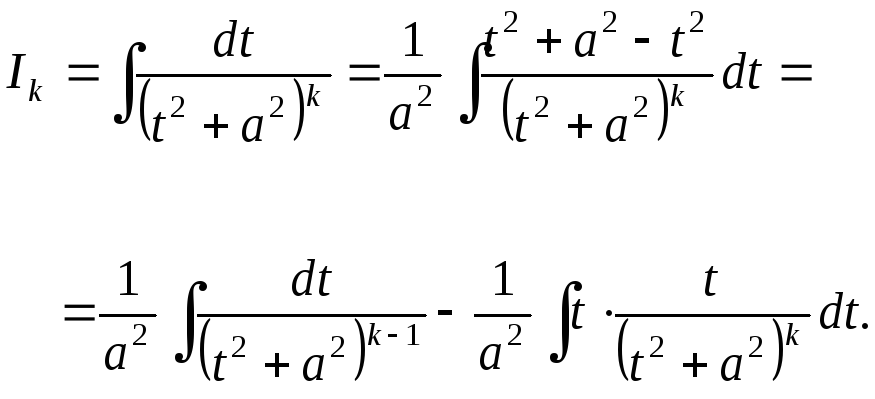
Ко
второму интегралу применим формулу
интегрирования по частям, положив
![]() ,
,![]() .
Тогда
.
Тогда![]() ,
а
,
а![]() – это уже вычисленный интеграл
– это уже вычисленный интеграл![]() .
Получим
.
Получим
![]() ,
,
![]() .
.
Из последнего равенства и получим рекуррентную формулу
![]() .
.
Эта
формула позволяет последовательно
вычислять интегралы ![]() для любого
для любого ![]() ,
опираясь на то, что
,
опираясь на то, что
![]() .
.
Вывод: интегралы от простейших рациональных дробей выражаются в конечном виде через рациональные дроби, логарифмы и арктангенсы.
III Интегрирование правильных рациональных дробей
Сформулируем (без доказательств) две теоремы алгебры, которые позволяют свести интегрирование правильных дробей к интегрированию простейших.
Теорема
1.
Всякий многочлен с действительными
коэффициентами можно разложить
единственным образом на множители двух
типов: а) ли-нейные ![]() ,
б) квадратичные
,
б) квадратичные ![]() ,
где
,
где ![]() – действи-тельные числа. Эти множители
могут быть простыми, если
– действи-тельные числа. Эти множители
могут быть простыми, если ![]() ,
и крат-ными, если
,
и крат-ными, если ![]() .
.
Отметим, что линейные множители соответствуют действительным корням многочлена, а квадратичные – парам комплексных сопряженных корней.
Теорема 2. Всякую правильную рациональную дробь можно разложить на сумму простейших дробей; при этом:
a) линейному простому множителю в разложении знаменателя дроби на множители соответствует дробь 1го типа ;
b) линейному кратному множителю соответствует сумма дробей 1го и 2го типов вида
;
c)
квадратичному простому множителю
![]() соответствует дробь 3го
типа ;
соответствует дробь 3го
типа ;
d)
квадратичному кратному множителю
![]() соот-ветствует сумма дробей 3го
и 4го
типа вида
соот-ветствует сумма дробей 3го
и 4го
типа вида
![]() .
.
Здесь
![]() ,
,
![]() ,
,
![]() – некоторые действительные числа, часть
из которых может быть равна 0.
Указанное разложение единственное (с
точностью до порядка слагаемых).
– некоторые действительные числа, часть
из которых может быть равна 0.
Указанное разложение единственное (с
точностью до порядка слагаемых).
Можно предложить следующий алгоритм разложения правильной дроби на простейшие слагаемые:
1) в соответствии с разложением знаменателя дроби на множители выписываем формальное разложение дроби на простейшие слагаемые с неизвестными коэффициентами;
2) приводим выписанную сумму дробей к общему знаменателю;
3) приравниваем числитель дроби, полученной в пункте 2), числителю исходной дроби;
4) равенство (тождественное!) многочленов, полученное в пункте 3) позволит нам найти неизвестные коэффициенты либо методом неопределенных коэффициентов ( т.е. приравнивая коэффициенты, стоящие при равных степенях х) либо методом частных значений (т.е. придавая переменной х конкретные – “ удобные ” – значения ).
Замечание. Метод частных значений особенно удобен в случае прос-тых действительных корней знаменателя разлагаемой дроби. Можно ком-бинировать оба метода определения неизвестных коэффициентов.
Примеры. 1. Разложить на простейшие слагаемые дробь
![]()
1й шаг: пишем формальное разложение
![]()
2й шаг: приводим сумму дробей к общему знаменателю
![]()
3й шаг: приравниваем числители
![]()
4й шаг: метод неопределенных коэффициентов дает систему уравнений

Отсюда
:![]() Искомое разложение имеет вид
Искомое разложение имеет вид
![]()
Теперь,
если понадобится, легко найти интеграл
![]()
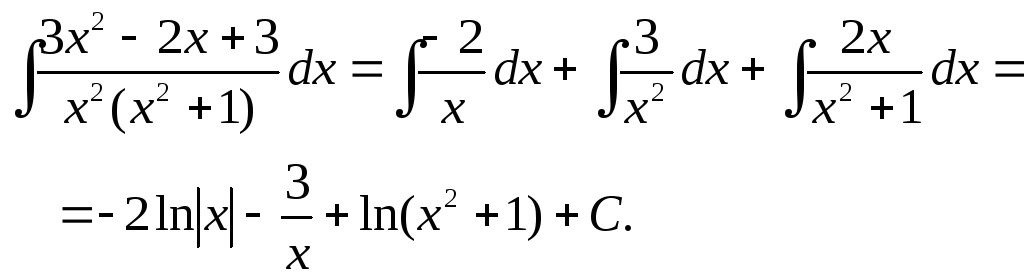
2.
Вычислить
![]() .
.
Имеем:
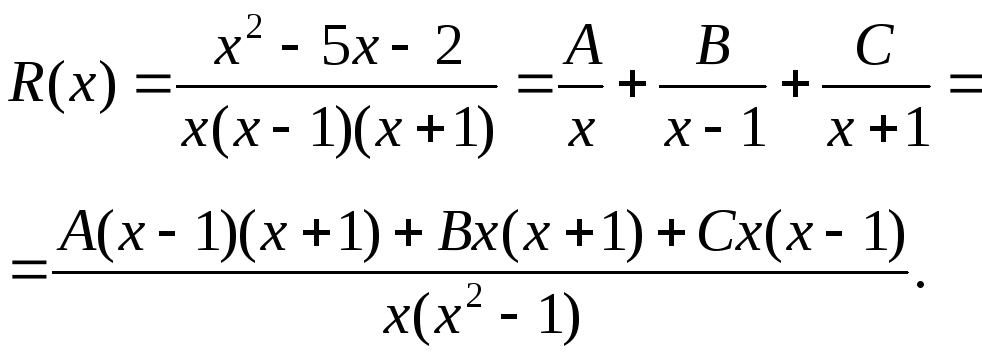
Отсюда следует тождество:
![]()
Для
определения коэффициентов положим в
этом тождестве последовательно
![]() .
Сразу получим:
.
Сразу получим:![]()
![]()
![]() ,
т.е.
,
т.е.
![]() ,
,![]() ,
,![]() .
Окончательно имеем:
.
Окончательно имеем:
![]()
3.
![]()
Разложение на простейшие дроби здесь достигается путем незамысловатых преобразований:
![]()
Искомый
интеграл равен
![]()
В заключение сформулируем основной результат данного параграфа: интегралы от рациональных функций выражаются в конечном виде с помощью рациональных функций, логарифмов и арктангенсов. Иными словами, всякая рациональная функция интегрируется в элементарных функциях.
В связи с этим интегралы от иррациональных и трансцендентных выражений стараются специально подобранными подстановками рационализировать, т.е. свести к интегралам от рациональных функций. Этим подстановкам и будут посвящены следующие параграфы.
