
- •§1. Первообразная и неопределенный интеграл: основные определения и теоремы
- •§2. Таблица основных интегралов
- •§3. Основные правила интегрирования
- •§4. Основные методы интегрирования
- •I Непосредственное интегрирование
- •II Метод замены переменной
- •II.1 Подведение под знак дифференциала
- •II.2 Метод подстановки
- •III Интегрирование по частям
- •§5. Интегрирование некоторых выражений, содержащих квадратный трехчлен
- •§6. Интегрирование рациональных функций
- •I Рациональные функции
- •1) ; 2); 3); 4).
- •II Интегрирование простейших дробей
- •III Интегрирование правильных рациональных дробей
- •§7. Интегрирование некоторых тригонометрических выражений
- •I Интегралы вида
- •II Интегралы вида
- •V Интегралы вида
- •III Квадратичные иррациональности: общий случай,
- •IV Интегрирование биномиальных дифференциалов:
V Интегралы вида
Для гиперболических функций имеются разнообразные формулы, аналогичные формулам тригонометрии. Приведем некоторые из них:
1)
основное тождество –
![]() ;
;
2)
формулы двойных углов –
![]() ;
;![]() ;
;
3)
формулы понижения степени –
![]() ,
,![]() .
.
Пользуясь
этими формулами нетрудно рационализировать
любой интеграл вида
![]() .
Однако, на практике иногда проще выразить
гиперболические функции через
показательную функцию
.
Однако, на практике иногда проще выразить
гиперболические функции через
показательную функцию
![]()
и
рационализировать интеграл подстановкой
![]() :
:
![]()
Примеры.
10.![]()
![]() .
.
11.
![]() .
.
§8. Интегрирование некоторых иррациональных выражений
I Линейные и дробно-линейные иррациональности
Пусть
![]() – линейная или дробно-линейная функция.
Интеграл вида
– линейная или дробно-линейная функция.
Интеграл вида![]() рационализируется подстановкой
рационализируется подстановкой![]() ,
где
,
где
![]() ,
так что числа
,
так что числа
![]() – целые. Например, если
– целые. Например, если![]() ,
то
,
то![]() ,
,![]() и
и![]() ,
где
,
где![]() – некоторая ра-циональная функция.
– некоторая ра-циональная функция.
Аналогично
нетрудно показать (рекомендуем сделать
это! ), что если
![]() ,
то
,
то![]() и
и![]() и интеграл
и интеграл![]() снова рационализируется.
снова рационализируется.
Пример 1.

![]() .
.
II Квадратичные иррациональности: частный случай
В
этой части параграфа рассмотрим интегралы
вида
![]() и
и![]() .
В этих интегралах удается избавиться
от иррациональности с помощью
тригонометрических или гиперболических
подстановок, после чего рационализировать
интеграл подстановками, рассмотренными
в предыдущем параграфе.
.
В этих интегралах удается избавиться
от иррациональности с помощью
тригонометрических или гиперболических
подстановок, после чего рационализировать
интеграл подстановками, рассмотренными
в предыдущем параграфе.
II.1

![]() .
.
С
тем же успехом можно взять и
![]() ,
,![]() .
.
II.2
a)

![]() ;
;
b)
![]() .
.
II.3
a)
![]() ;
;
b)
![]() .
.
Относительно
интеграла
![]() необходимо сделать следующее замечание.
Область определения радикала
необходимо сделать следующее замечание.
Область определения радикала![]() состоит из 2-х частей:
состоит из 2-х частей:![]() .
Рассмотренные выше замены справедливы
лишь для
.
Рассмотренные выше замены справедливы
лишь для![]() .
Для
.
Для![]() тригонометрическая замена та же, но
тригонометрическая замена та же, но![]() и
и![]() ,
а гиперболическая замена имеет вид
,
а гиперболическая замена имеет вид![]() .
В случае четной или нечетной подынтегральной
функции можно пользоваться соответствующими
свойствами первообразных (см. §1) и не
рассматривать отдельно случай
.
В случае четной или нечетной подынтегральной
функции можно пользоваться соответствующими
свойствами первообразных (см. §1) и не
рассматривать отдельно случай![]() .
.
Примеры.

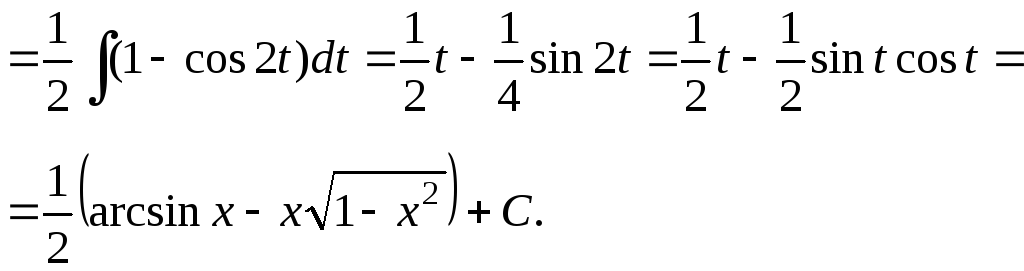
3.
![]()
![]()
Если
учесть, что ![]() ,
то ответ можно упростить
,
то ответ можно упростить
![]()
![]() .
.
4.
![]() .
Здесь тригонометрическая замена
приведет к сложно-му интегралу
.
Здесь тригонометрическая замена
приведет к сложно-му интегралу![]() ,
поэтому лучше применить гиперболическую
подстановку:
,
поэтому лучше применить гиперболическую
подстановку:![]() ,
,![]() ,
,![]() .
Имеем
.
Имеем
![]()
![]() .
.
Здесь
на последнем шаге использована формула
для
![]() и выражение
и выражение![]() через логарифм.
через логарифм.
5.
![]() .
.
Для
![]() сделаем замену
сделаем замену![]() ,
,![]() ,
тогда
,
тогда![]() ,
,![]() ,
,![]() и получим
и получим
![]()
![]() .
.
Подынтегральная
функция – четная, а полученная
первообразная нечетная, значит результат
справедлив и для
![]() .
.
III Квадратичные иррациональности: общий случай,
подстановки Эйлера
Интеграл
вида
![]() выделением полного квадрата в подкоренном
выражении и соответствующей заменой
переменной можно свести к одному из
интегралов, рассмотренных ранее.
выделением полного квадрата в подкоренном
выражении и соответствующей заменой
переменной можно свести к одному из
интегралов, рассмотренных ранее.
Однако,
существуют и прямые способы рационализации
интеграла – это так называемые подстановки
Эйлера. Новая переменная интегрирования
![]() вводится такими соотношениями:
вводится такими соотношениями:
1)
если
![]() ,
то
,
то![]() ;
;
2)
если
![]() ,
то
,
то![]() ;
;
3)
если
![]() ,
то
,
то![]() ,
где
,
где![]() – один из корней квадратного трехчлена.
– один из корней квадратного трехчлена.
Возводя
эти
соотношения в квадрат и упрощая, можно
убедиться в том, что
![]() ,
,
![]() и
радикал
и
радикал
![]() выражается через
выражается через
![]() рациональным
образом. Следовательно, данный интеграл
рационализируется.
рациональным
образом. Следовательно, данный интеграл
рационализируется.
Предлагается студентам самостоятельно произвести все необходимые преобразования и применить эти подстановки к вычислению интегралов:
![]() ,
,
![]() ,
,![]() .
.
