
ТВМС расчетное 4Э41
.pdfкредита в генеральной совокупности.
24.Производится обследование на предмет среднего времени просмотра телепередач с 8 до 17 часов. Каким должен быть объем выборки, чтобы отклонение выборочной средней от генеральной не превышало 4 минут (по абсолютной величине) с вероятностью 0.9? Если
впредыдущих исследованиях средне стандартное отклонение времени просмотра передач составило 22 минут.
25.Изготовлен игровой автомат, который должен обеспечить выигрыш в одном случае из 100. Произведено 640 испытаний, количество выигрышей 6. Найти доверительный интервал для вероятности выигрыша с надежностью 0.975.
26.Заключение страховых договоров в 140 филиалах страховых компаний составило 40000 штук в регионе А. В регионе В, в 200 филиалах составило 40000. Средне квадратические отклонения количества заключенных страховых полисов в регионах А и В, равны соответственно 15000 и 13500. Проверить на уровне значимости 0.001 существенно ли различаются регионы по количеству заключенных страховых договоров.
27.Доля убыточных предприятий в 2000 году в России в среднем составила 30%.
В одном из регионов России 36%. В 2006 году в этой области было 9014 предприятий. На уровне значимости 0.1 и 0.075 проверить, существенны ли различия в удельном весе убыточных предприятий в данном регионе по сравнению с общероссийским или нет.
28.В 2000 году доля предприятий государственной формы собственности в одном из регионов Российской Федерации составила 2.7%. Среди 2800 машиностроительных
иметаллургических предприятий этого региона она оказалась равной 2.9%. На уровне значимости 0.1 и 0.01 проверить существенно ли различие удельного веса государственной формы собственности для всех предприятий в целом и для предприятий машиностроения
иметаллургии.
29.В рекламе утверждается, что средне месячный доход по акциям компании А превышает доход по акциям компании В более чем на 0.1%. В течении года средне месячный доход по акциям этих компаний составил 0.57% и 0.25% соответственно. Средне квадратические отклонения одинаковы. На уровне значимости 0.075 и 0.025 проверить справедливость рекламы.
30.Производитель некоторой продукции утверждает, что 91% его продукции не имеют дефектов. Случайная выборка из 70 изделий показала, что 66 изделий не имеют дефектов. Проверить на уровне значимости 0.1336 справедливость претензий производителя.
31.Некоторая компания, производящая средства для похудания, утверждает, что при приеме ее продукции в сочетании со специальной диетой позволяет сбросить в неделю, в среднем 450 грамм. Для проведения экспертизы случайным образом отобрано 55 человек. После проведения эксперимента обнаружено, что в среднем еженедельный сброс веса составил 430 грамм, исправленное среднеквадратическое отклонение составило 200 грамм. Проверить гипотезу от том, что средняя еженедельная потеря веса составляет 450 грамм. Принять уровень значимости равный 0.05.
Вариант № 4 Белкин
1.Найдите вероятность того, что наудачу выбранное 2-значное число не содержит ни одной 5.
2.Имеется 6 различных флага. На флагштоке поднимается сигнал, состоящий не менее чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке (порядок флагов учитывается)?
3.Сколько различных линий можно провести через 9 точек, из которых никакие три не лежат на одной прямой?
4.Группа студентов из 4 юношей и 5 девушек выбирает по жребию хозяйственную команду в составе четырех человек. Какова вероятность того, что в составе этой команды
10

окажутся два юноши и две девушки?
5.Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше 1, не превзойдет единицы, а их произведение будет не больше 0.11.
6.В ящике 35 деталей, из них 6 бракованных. Наудачу извлечены 6 детали. Найти вероятность того, что среди извлеченных деталей:а)нет бракованных; б) нет годных; в) ровно 3 годных.
7.В городе имеется четыре коммерческих банка, оценка надежности которых 0.8; 0.7; 0.9; 0.9 соответственно. Администрацию города интересуют ответы на вопросы: а) какова вероятность того, что в течении года обанкротятся три банка; б) хотя бы один банк.
8.Вероятность совершения покупки первым покупателем равна 0.9 а вторым - 1.. Какова вероятность того, что будет совершена хотя бы одна покупка, если они совершаются независимо друг от друга?
9.В урне 4 белых и 4 черных шара. Из нее вынимаются подряд два шара. Найти вероятность того, что оба шара белые.
10.Покупатель проходит мимо 2 трех расположенных подряд стеллажей с товарами и совершает или не совершает покупку. Вероятность покупки товара на первом стеллаже 0.9
иуменьшается на 0.05 при каждом последующем стеллаже. Какова вероятность получить ровно две покупки?
11.Сколько нужно поставить дублирующих приборов с той же надежностью 0.2, что
иосновной, чтобы надежность системы приборов была не ниже заданной величины 0.9?
12.Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0.8 для первого сигнализатора
и0.9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
13.В пирамиде n1 винтовок, m1 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом,
равна p1; для винтовки без оптического прицела эта вероятность равна q1. Найти вероятность того,что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
14.Имеется две партии изделий по n2 и m2 штук, причем в первой партии одно изделие бракованное, а во второй партии два изделия бракованные. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.
15.Пусть в условиях задачи 14 известно, что извлеченное из второй партии изделие – бракованное. Определить вероятность того, что при этом из первой партии было извлечено так же бракованное изделие.
n1 = 17, m1 = 11, p1 = 2150 , q1 = 254 ; n2 = 9, m2 = 8;
16. Случайная величина X задана на всей оси OX функцией распределения tan¡1(x) +
¼
12 . Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале [4; 9]. Найти вероятность того, что в результате испытания 6 раз независимых испытаний величина X ровно 2 раза примет значение, заключенное в интервале [4; 9] (точность 3 знака после запятой).
17. Дискретная случайная величина X имеет таблицу распределения
xi |
-3 |
|
-2 |
-1 |
0 |
|
1 |
|
2 |
3 |
|
4 |
|
|||||||||
pi |
|
1 |
|
|
1 |
|
|
8 |
|
|
4 |
|
|
37 |
|
14 |
|
17 |
|
|
1 |
|
150 |
|
15 |
|
75 |
15 |
150 |
75 |
150 |
|
150 |
||||||||||||
Найти P(X > 0). Найти P(jXj < 2). Пусть Y = X2. Найти математическое ожидание и дисперсию величины Y . (точность 3 знака после запятой).
11
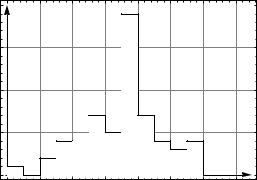
|
Произведена выборка 60 роликов. По данным |
|
|
|
|
|
|
|
|
|
|||||||
|
отклонений X |
мм от |
номинального |
размера 20 |
|
ni |
|
|
|
|
|
|
|||||
|
их диаметров построена гистограмма частот. |
|
|
|
|
|
|
|
|
|
|||||||
|
1). Найти число роликов, |
удовлетворяющее 15 |
|
|
|
|
|
|
|
|
|||||||
|
неравенству 0 |
· X |
· 3. |
2). Найти |
моду |
|
|
|
|
|
|
|
|
|
|||
18. |
выборочного |
распределения. |
3). |
Найти 10 |
|
|
|
|
|
|
|
|
|||||
медиану |
выборочного |
распределения. |
4). |
|
|
|
|
|
|
|
|
|
|||||
|
Найти среднее выборочное значение. 5). |
5 |
|
|
|
|
|
|
|
|
|||||||
|
Найти выборочную дисперсию. 6). Найти |
|
|
|
|
|
|
|
x |
||||||||
|
коэффициент |
асимметрии. |
7). |
Найти |
0 |
|
|
|
|
|
|
|
|||||
|
коэффициент |
эксцесса. Дать |
их смысловую |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||||
|
нагрузку. (точность 3 знака после запятой). |
|
|
|
|
|
|
|
|
|
|||||||
19.
Дана себестоимость $X единицы
продукции |
|
для 80 |
предприятий. |
0 |
|
|
|
|
|
|
|
|
1 |
|||||||||
Построить вариационный ряд, взять |
4:1 4:87 5:26 6:42 5:36 5:69 5:59 |
6:06 |
||||||||||||||||||||
число интервалов равным 8 . Найти: |
||||||||||||||||||||||
4:56 |
6:62 |
4:2 |
5:59 |
5:99 |
5:31 |
5:77 |
6:07 |
|||||||||||||||
1). медиану. 2). среднее выборочное |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
4:83 |
6:52 |
5:12 |
5:66 |
5:12 |
3:53 |
6:22 |
6:49 |
C |
|
X |
|
|
|
|
|
|
|
|
|
|
|
B |
7:03 |
6:96 |
10 |
5:94 |
6:07 |
7:07 |
4:76 |
4:56 |
C |
|
значение. 3). выборочную дисперсию. |
B |
C |
||||||||||||||||||||
4). Построить |
гистограмму частот |
B |
|
|
|
|
|
|
|
|
C |
|||||||||||
B |
4:3 |
5:27 |
5:45 |
6:13 |
6:35 |
5:65 |
6:63 |
6:11 |
C |
|||||||||||||
|
. |
Исходя |
|
из |
|
группировки |
B |
|
|
|
|
|
|
.5:85 |
|
C |
||||||
|
|
|
B |
2 |
4:48 |
2:75 |
6:23 |
3:67 |
6:62 |
6:15 |
C |
|||||||||||
данных в |
гистограмме найти: |
5). |
B |
|
|
|
|
|
|
|
|
C |
||||||||||
B |
5:47 |
5:81 |
3:17 |
3:88 |
5:78 |
5:05 |
4:52 |
4:39 |
C |
|||||||||||||
число |
|
|
2 |
|
X |
|
4 |
|
которых |
B |
7:01 |
7:19 |
4:82 |
7:3 |
3:7 |
5:32 |
6:41 |
4:54 |
C |
|||
предприятий |
для |
|
B |
C |
||||||||||||||||||
себестоимость |
· |
|
· |
|
|
|
|
B |
4:29 |
5:93 3:08 |
4:04 |
4:29 |
5:95 5:08 |
7:21 |
C |
|||||||
|
|
удовлетворяет |
B |
C |
||||||||||||||||||
неравенству |
|
|
|
|
|
. |
6). моду |
B |
5:94 |
6:22 |
5:74 |
6:95 |
5:13 |
6:84 |
3:29 |
5:49 |
C |
|||||
выборочного |
|
распределения. |
7). |
@ |
|
|
|
|
|
|
|
|
A |
|||||||||
коэффициент |
|
асимметрии. |
8). |
|
|
|
|
|
|
|
|
|
|
|||||||||
коэффициент эксцесса.
20.В целях изучения среднедушевого дохода семей в 2000 году была произведена 2% выборка из 17 тысяч семей. По результатам обследования среднедушевой доход семьи составил 14 тысяч рублей, со среднеквадратическим отклонением, равным 4 тысяч рублей.
Найти 99.9% доверительный интервал, покрывающий неизвестный генеральный среднедушевой доход, генеральная совокупность подчинена нормальному закону распределения.
21.Для изучения демографических исследований обследовали 260 семей. Оказалось,что среди обследованных 36% составляют семьи из трех человек. Найти 95.% доверительный интервал для генеральной доли числа семей состоящей из трех человек.
22.Производится обследование на предмет среднего времени просмотра телепередач с 6
до 17 часов. Каким должен быть объем выборки, чтобы отклонение выборочной средней от генеральной не превышало 5 минут (по абсолютной величине) с вероятностью 0.95? Если в предыдущих исследованиях средне стандартное отклонение времени просмотра передач составило 20 минут.
23.В 2002 году выборочное обследование ХМАО показало, что 15% обследованных имеют среднедушевой доход не более 20 тысяч рублей. В каких границах находится доля населения, имеющая такой же доход, если объем генеральной выборки 42 тысяч, выборка не более 12% и осуществляется случайным бесповторным выбором, доверительная вероятность 0.95.
24.При выборочном опросе 1900 телезрителей оказалось,что 420 из них предпочитают программы НТВ. Построить 99.% доверительный интервал, покрывающий генеральную долю числа зрителей, предпочитающих программы НТВ.
25.Менеджер компании, занимающийся прокатом автомобилей, оценивает среднюю величину пробега одного автомобиля в течении месяца. Из 400 автомобилей компании
12
с помощью бесповторной выборки отобрано 30 автомобилей. Установлено, что средний пробег автомобиля составляет 1900 км, со стандартным отклонением 120 км. Найти 99.9% доверительный интервал покрывающий средний пробег автомобилей всего парка в течении месяца.
26.Крупный коммерческий банк заказал маркетинговое исследование по выявлению эффекта <премирования> (канцелярские принадлежности) для стимула при открытии счета в банке. Для проверки случайным образом было отобрано по 180 посетителей, получивших премию и не получивших. В результате оказалось, что среди посетителей, которым не предлагалась премия 66% и среди посетителей, которым предлагалась премия, 72% открывали счета в данном банке, в течении 3 месяцев. На уровне значимости 0.075 и
0.01проверить существенно премирование или нет.
27.Инвестиционная компания не осуществляет вложении в ценные бумаги если среднеквадратическое отклонение годового дохода более чем 0.21%. Эта компания провела 71 наблюдений по активу А и получила, что среднеквадратическое отклонение годовой доходности составило 0.29%. На уровне доверия выяснить допустимы ли вложения в актив А на уровне значимости 0.05;0.1?
28.Компания по производству весов для торговых предприятий утверждает, что точность весов, измеряющих продукты питания весом до 8кг, составляет 3 грамма. В торговое предприятие поступила на пробу опытная партия из 19 таких весов. По результатам взвешиваний одного продукта получили,что исправленное средне квадратическое отклонение равно 3.5 грамма. Проверить справедливость утверждения компании на уровне значимости 0.075 и 0.1.
29.В магазин поступила новая партия видеомагнитофонов. Для проверки случайным образом было отобрано n5 видеомагнитофонов. Среднее время бесперебойной работы составило 9900 часов. Средне квадратическое отклонение бесперебойной работы видеомагнитофона по данным компании производителя составляет 1400 часов. Можно ли на уровне доверия 0.05% принять гипотезу о том, что среднее время бесперебойной работы равно 9300 часов.
30.Доля убыточных предприятий в 2000 году в России в среднем составила 34%. В одном из регионов России 38%. В 2006 году в этой области было 8434 предприятий. На уровне значимости 0.05 и 0.1336 проверить, существенны ли различия в удельном весе убыточных предприятий в данном регионе по сравнению с общероссийским или нет.
31.Фирма посредник рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность заказа товара, при условии получения каталога, равна 0.14. Фирма разослала 800 каталогов новой улучшенной формы и получила 130 заказов. На уровне доверия 86.64% и 99.9% существенна ли новая форма каталога или нет.
Вариант № 5 Берестнев
1.Найдите вероятность того, что наудачу выбранное 2-значное число не содержит ни одной 4.
2.Группа студентов из 5 юношей и 6 девушек выбирает по жребию хозяйственную команду в составе четырех человек. Какова вероятность того, что в составе этой команды окажутся два юноши и две девушки?
3.Два студента условились встретиться в определенном месте между 13 и 15 часами
дня. Пришедший первым ждет второго в течении 13 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 13 до 15 часов).
4.В ящике 38 деталей, из них 8 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей:а)нет бракованных; б) нет годных; в) ровно 3 годных.
13

5.Устройство состоит из 7 элементов, из которых 4 изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
6.Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше 94 , а частное xy не
больше 114 .
7.Студент знает 10 из 17 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
8.Реклама растворимого кофе <Гранд> предается по каналам ОРТ, РТР, НТВ. Вероятность того, что потребитель увидит эту рекламу на канале ОРТ, равна 0.6; на РТР - 1. и на канале НТВ - 0.9. Найти вероятность того, что потребитель увидит эту рекламу:а) по всем трем каналам; б) хотя бы по одному из этих каналов.
9.По каналу связи передается 4 сообщений. Каждое из них (независимо от других) с вероятностью 0.6 искажается. Найти вероятность следующих событий: а) A - все сообщения переданы без искажений; б) B - все сообщения будут искажены; в) C - не менее двух сообщений будет искажено.
10.Вероятность совершения покупки первым покупателем равна 0.6 а вторым - 0.6. Какова вероятность того, что будет совершена хотя бы одна покупка, если они совершаются независимо друг от друга?
11.Компания имеет два независимых источника электроэнергии для использования в случае аварийного отключения постоянного источника электроэнергии. Вероятность того, что первый из этих резервных источников будет доступен и исправен равна 0.8; второй -
0.8.Найти вероятность того, что не произойдет отключения электроэнергии, если выйдет из строя постоянный источник.
12.Аналитики торговой компании считают, что покупатели, обладающие дисконтной картой этой компании, обратятся в магазины этой компании с вероятностью 0.3. Если это произойдет, то покупатель совершает покупку с вероятностью 0.8. Найти вероятность того, что покупатель обладающий дисконтной картой этой компании совершит покупку.
13.В пирамиде n1 винтовок, m1 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом,
равна p1; для винтовки без оптического прицела эта вероятность равна q1. Найти вероятность того,что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
14.Имеется две партии изделий по n2 и m2 штук, причем в первой партии одно изделие бракованное, а во второй партии два изделия бракованные. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.
15.Пусть в условиях задачи 14 известно, что извлеченное из второй партии изделие – бракованное. Определить вероятность того, что при этом из первой партии было извлечено так же бракованное изделие.
n1 = 15, m1 = 8, p1 = 259 , q1 = 501 ; n2 = 3, m2 = 11;
16. Дискретная случайная величина X задана законом распределения
xi |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
6 |
|
7 |
|
||||||
pi |
|
1 |
|
|
3 |
|
|
7 |
|
|
7 |
|
1 |
|
7 |
|
|
1 |
|
30 |
40 |
30 |
|
24 |
|
5 |
60 |
20 |
|
||||||||||
Найти функцию распределения и построить ее график. Найти математическое ожидание и дисперсию величины X (точность 3 знака после запятой).
14

17. Случайная величина X задана функцией распределения |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0; |
(x + 4)4; |
|
x · ¡4 |
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
F (x) = 8811 |
|
4 < x |
· ¡ |
|
|
|
|
|
|
||||||||
|
|
|
|
|
> |
|
|
¡ |
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
<1; |
|
|
x > |
¡ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти вероятность того, что в |
результате испытания величина X примет значение, заключенное |
|||||||||||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в интервале [¡3; 1]. Найти математическое ожидание и дисперсию величины X. |
|
|
||||||||||||||||||
|
Произведена выборка 90 роликов. По данным |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
отклонений X |
мм от |
|
номинального размера |
|
|
|
ni |
|
|
|
|
|
|
||||||
|
их диаметров построена гистограмма частот. |
15 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1). Найти число роликов, удовлетворяющее |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
неравенству 1 |
· X |
|
· 2. 2). Найти |
|
моду |
10 |
|
|
|
|
|
|
|
|
|
||||
18. |
выборочного |
распределения. |
3). |
Найти |
|
|
|
|
|
|
|
|
|
|
|
|||||
медиану |
выборочного |
распределения. |
4). |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Найти среднее выборочное значение. 5). |
5 |
|
|
|
|
|
|
|
|
|
|||||||||
|
Найти выборочную дисперсию. 6). Найти |
|
|
|
|
|
|
|
|
|
|
x |
||||||||
|
коэффициент |
асимметрии. |
7). |
Найти |
0 |
|
|
|
|
|
|
|
|
|||||||
|
коэффициент эксцесса. Дать их смысловую |
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||||||||
|
нагрузку. (точность 3 знака после запятой). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
19.
Дана себестоимость $X единицы
продукции |
|
для 80 |
предприятий. |
0 |
|
|
|
|
|
|
|
|
1 |
|||||||||
Построить вариационный ряд, взять |
4:41 |
7:41 |
4:66 |
5:59 |
4:56 |
7:15 |
5:66 |
5:54 |
||||||||||||||
число интервалов равным 6 . Найти: |
||||||||||||||||||||||
6:01 |
6:49 |
5:59 |
5:96 |
5:55 |
3:81 |
5:29 |
3:77 |
|||||||||||||||
1). медиану. 2). среднее выборочное |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
7:41 |
5:88 |
6:25 |
6:47 |
5:44 |
7:07 |
5:53 |
6:66 |
C |
|
X |
|
|
|
|
|
|
|
|
|
|
|
B |
5:47 |
5:28 |
6:79 |
4:68 |
5:37 |
4:83 |
5:94 |
3:53 |
C |
|
значение. 3). выборочную дисперсию. |
B |
C |
||||||||||||||||||||
4). Построить |
гистограмму частот |
B |
|
|
|
|
|
|
|
|
C |
|||||||||||
B |
4:99 |
3:69 |
5:4 |
6:88 |
5:63 |
5:38 |
2 |
5:24 |
C |
|||||||||||||
|
. |
Исходя |
|
из |
|
группировки |
B |
|
|
|
|
|
|
.5:74 |
|
C |
||||||
|
|
|
B |
3:82 |
2:81 |
4:26 |
7:49 |
7: |
4:93 |
3:91 |
C |
|||||||||||
данных в |
гистограмме найти: |
5). |
B |
|
|
|
|
|
|
|
|
C |
||||||||||
B |
7:09 |
5:52 |
7:06 |
5:92 |
4:41 |
5:6 |
5:64 |
7:46 |
C |
|||||||||||||
число |
|
|
2 |
|
X |
|
3 |
|
которых |
B |
8 |
3:29 |
4:47 |
5:5 |
4:92 |
4:79 |
5:44 |
3:36 |
C |
|||
предприятий |
для |
|
B |
C |
||||||||||||||||||
себестоимость |
· |
|
· |
|
|
|
|
B |
6:66 |
2:88 4:46 |
3:93 |
4:31 |
5:67 5:79 |
5:41 |
C |
|||||||
|
|
удовлетворяет |
B |
C |
||||||||||||||||||
неравенству |
|
|
|
|
|
. |
6). моду |
B |
5:17 |
4:89 |
4:95 |
4:94 |
5:44 |
5:51 |
5:01 |
7:17 |
C |
|||||
выборочного |
|
распределения. |
7). |
@ |
|
|
|
|
|
|
|
|
A |
|||||||||
коэффициент |
|
асимметрии. |
8). |
|
|
|
|
|
|
|
|
|
|
|||||||||
коэффициент эксцесса.
20.Коммерческий банк, изучая возможность предоставления долгосрочных кредитов населению, проводит опрос своих клиентов для определения размеров такого рода кредитов.
Вбанке 16000 клиентов. Опрошено 13% с помощью бесповторной выборки. Среднее значение необходимого кредита составило 170 тысяч рублей, со стандартным отклонением в 36 тысяч рублей. Найти 95.% доверительный интервал для оценки среднего значения кредита в генеральной совокупности.
21.При исследовании доходов населения города в 26000 чел., в случае бесповторной выборки для 1500 чел. получены распределения доходов.
xi |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
5000 |
5500 |
6000 |
ni |
1 |
9 |
84 |
349 |
571 |
376 |
97 |
12 |
1 |
Найти границы среднего дохода с надежностью 90.%. Каким должен быть объем выборки,чтобы гарантировать те же границы с надежностью 0.999?
22. При выборочном опросе 1100 телезрителей оказалось,что 600 из них предпочитают программы НТВ. Построить 99.9% доверительный интервал, покрывающий генеральную долю числа зрителей, предпочитающих программы НТВ.
15
23.Для изучения размера среднемесячной заработной платы проводится повторная выборка. Каким должен быть объем этой выборки, что бы с вероятностью 0.975 можно было утверждать, что выборочная средняя зарплата отличается от генеральной средней заработной платы по абсолютной величине не более чем на 16%. Выборочная средняя заработная плата равна 23 тысяч рублей, среднеквадратическое отклонение равно 10 тысяч рублей.
24.Аудиторская фирма получила заказ на контроль состояния счетов некоторого банка. Для этого случайно отбираются 80 счетов. По 56 из них имело движение денежных средств в течении месяца. Найти 99.% доверительный интервал, оценивающий долю счетов
вгенеральной совокупности, по которым имело место движение денежных средств в течении месяца.
25.Изготовлен игровой автомат, который должен обеспечить выигрыш в одном случае из 170. Произведено 800 испытаний, количество выигрышей 6. Найти доверительный интервал для вероятности выигрыша с надежностью 0.975.
26.Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар будет замене сукразитом. Компания хотела бы быть уверенной, что не менее 75% ее потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 900 человек, и 648 человека сказали, что новый напиток вкуснее старого. Может ли на уровне значимости 0.025 компания принять новый напиток в производство.
27.Производитель некоторой продукции утверждает, что 85% его продукции не имеют дефектов. Случайная выборка из 70 изделий показала, что 68 изделий не имеют дефектов. Проверить на уровне значимости 0.0027 справедливость претензий производителя.
28.Инвестиционная компания не осуществляет вложении в ценные бумаги если среднеквадратическое отклонение годового дохода более чем 0.23%. Эта компания провела 90 наблюдений по активу А и получила, что среднеквадратическое отклонение годовой доходности составило 0.28%. На уровне доверия выяснить допустимы ли вложения в актив А на уровне значимости 0.01;0.0027?
29.Фирма посредник рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность заказа товара, при условии получения каталога, равна 0.16. Фирма разослала 800 каталогов новой улучшенной формы и получила 100 заказов. На уровне доверия 86.64% и 92.5% существенна ли новая форма каталога или нет.
30.В 2000 году доля предприятий государственной формы собственности в одном из регионов Российской Федерации составила 2.9%. Среди 2000 машиностроительных и металлургических предприятий этого региона она оказалась равной 3.1%. На уровне значимости 0.1336 и 0.1 проверить существенно ли различие удельного веса государственной формы собственности для всех предприятий в целом и для предприятий машиностроения и металлургии.
31.Заключение страховых договоров в 190 филиалах страховых компаний составило 38000 штук в регионе А. В регионе В, в 140 филиалах составило 23000. Средне квадратические отклонения количества заключенных страховых полисов в регионах А и В, равны соответственно 14500 и 14000. Проверить на уровне значимости 0.001 существенно ли различаются регионы по количеству заключенных страховых договоров.
Вариант № 6 Воложанинова
1.В ящике 37 деталей, из них 8 бракованных. Наудачу извлечены 6 детали. Найти вероятность того, что среди извлеченных деталей:а)нет бракованных; б) нет годных; в) ровно 2 годных.
2.Пассажирский поезд состоит из 3 багажных вагонов, 6 плацкартных и 7 купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться
16
вего начале, а купированные - в конце.
3.Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше 3, а частное xy не
больше 72 .
4.5 человек рассаживаются в ряд в случайном порядке. Какова вероятность, что два определенных лица окажутся рядом? Найти соответствующую вероятность, если те же лица садятся за круглый стол (места за круглым столом пронумерованы).
5.Какое число различных парных нарядов можно назначить из бригады в 10 человек? Сколькими способами можно составить такой наряд, если один из двух членов бригады должен быть назначен старшим?.
6.Найдите вероятность того, что наудачу выбранное 3-значное число не содержит ни одной 1.
7.Вероятность совершения покупки первым покупателем равна 0.6 а вторым - 0.5. Какова вероятность того, что будет совершена хотя бы одна покупка, если они совершаются независимо друг от друга?
8.Устройство состоит из трех элементов, работающих независимо.Вероятность безотказной работы (за время) первого, второго и третьего элементов соответственно равны 0.6, 1. и
0.8.Найти вероятность того, что за время безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.
9.Реклама растворимого кофе <Гранд> предается по каналам ОРТ, РТР, НТВ. Вероятность того, что потребитель увидит эту рекламу на канале ОРТ, равна 0.6; на РТР - 0.8 и на канале НТВ - 0.9. Найти вероятность того, что потребитель увидит эту рекламу:а) по всем трем каналам; б) хотя бы по одному из этих каналов.
10.По каналу связи передается 7 сообщений. Каждое из них (независимо от других) с вероятностью 0.7 искажается. Найти вероятность следующих событий: а) A - все сообщения переданы без искажений; б) B - все сообщения будут искажены; в) C - не менее двух сообщений будет искажено.
11.В электрическую цепь последовательно включены три элемента,работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны: 0.9, 0.8, 0.6. Найти вероятность того, что сигнал цепь а) пройдет, б) не пройдет.
12.Инвестор полагает, что в следующем периоде вероятность роста акций компании А будет 0.66. Вероятность того, что цены поднимутся на акции компаний А и В равна 0.56. Вероятность роста акций хотя бы одной из этих компаний равна 0.9. Найти вероятность роста акций компании В.
13.В пирамиде n1 винтовок, m1 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом,
равна p1; для винтовки без оптического прицела эта вероятность равна q1. Найти вероятность того,что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
14.Имеется две партии изделий по n2 и m2 штук, причем в первой партии одно изделие бракованное, а во второй партии два изделия бракованные. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.
15.Пусть в условиях задачи 14 известно, что извлеченное из второй партии изделие – бракованное. Определить вероятность того, что при этом из первой партии было извлечено так же бракованное изделие.
n1 = 18, m1 = 13, p1 = 4350 , q1 = 1125 ; n2 = 12, m2 = 14;
16. Дискретная случайная величина X имеет таблицу распределения
17
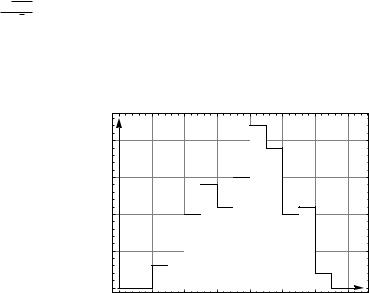
xi |
-3 |
|
-2 |
-1 |
0 |
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
||||||||||
pi |
|
1 |
|
|
1 |
|
|
1 |
|
|
3 |
|
1 |
|
7 |
|
|
11 |
|
|
1 |
|
|
1 |
|
120 |
|
60 |
|
12 |
10 |
4 |
30 |
|
120 |
|
120 |
|
120 |
|
|||||||||||
Найти P(X > 0). Найти P(jXj |
< 2). Пусть Y = X2. Найти математическое ожидание |
||||||||||||||||||||||
и дисперсию величины Y . (точность 3 знака после запятой). |
|
|
|
|
|
|
|||||||||||||||||
17. Случайная величина X задана функцией распределения |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
8 |
04; |
|
|
x · ¡1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
F |
( |
x |
) = |
px+1 |
; |
|
1 |
< x |
· |
1 |
|
|
|
|
|
|
||||
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
> |
|
|
¡ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
<1; |
|
|
x > 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти вероятность того, что в |
результате испытания величина X примет значение, заключенное |
||||||||||||||||||||||
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в интервале [0; 2]. Найти математическое ожидание и дисперсию величины X. |
|
|
|
||||||||||||||||||||
Произведена выборка 120 роликов. По данным |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
отклонений X мм от номинального |
|
размера |
|
|
|
ni |
|
|
|
|
|
|
|||||||||||
их диаметров |
построена |
|
гистограмма |
частот. |
20 |
|
|
|
|
|
|
|
|
||||||||||
1). Найти число роликов, удовлетворяющее |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
неравенству 1 |
· X |
· 3. 2). Найти |
моду 15 |
|
|
|
|
|
|
|
|
||||||||||||
выборочного |
распределения. |
|
3). |
|
Найти |
|
|
|
|
|
|
|
|
|
|
||||||||
18. медиану |
выборочного |
|
распределения. |
|
4). 10 |
|
|
|
|
|
|
|
|
||||||||||
Найти среднее выборочное значение. 5). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Найти выборочную дисперсию. 6). Найти |
|
5 |
|
|
|
|
|
|
|
x |
|||||||||||||
коэффициент |
асимметрии. |
|
7). |
|
Найти |
|
0 |
|
|
|
|
|
|
|
|||||||||
коэффициент эксцесса. Дать их смысловую |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||||||||||||
нагрузку. (точность 3 знака после запятой). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
19.
Дана себестоимость $X единицы
продукции |
|
для 80 |
предприятий. |
0 |
|
|
|
|
|
|
|
|
1 |
|||||||||
Построить вариационный ряд, взять |
5:58 |
7:57 |
7:06 |
5:31 |
6:35 |
5:76 |
6:13 |
5:11 |
||||||||||||||
число интервалов равным 7 . Найти: |
||||||||||||||||||||||
5:94 |
5:97 |
3:91 |
6:19 |
4:35 |
4:82 |
4:77 |
2:58 |
|||||||||||||||
1). медиану. 2). среднее выборочное |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
6:23 5:96 4:74 4:69 4:86 7:82 6:55 6: |
C |
||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
B |
3:61 |
5:52 |
4:23 |
4:55 |
7:43 |
3:47 |
4:49 |
4:13 |
C |
|
значение. 3). выборочную дисперсию. |
B |
C |
||||||||||||||||||||
4). Построить |
гистограмму частот |
B |
|
|
|
|
|
|
|
|
C |
|||||||||||
B |
6:55 |
5:96 |
5:2 |
7:79 |
4:12 |
4:7 |
6:67 |
7:43 |
C |
|||||||||||||
|
. |
Исходя |
|
из |
|
группировки |
B |
|
|
|
|
|
|
.7:91 |
|
C |
||||||
|
|
|
B |
5:05 |
3:89 |
7:5 |
9 |
7:59 |
4:53 |
4:43 |
C |
|||||||||||
данных в |
гистограмме найти: |
5). |
B |
|
|
|
|
|
|
|
|
C |
||||||||||
B |
4:6 |
5:48 |
4:37 |
3:95 |
3:08 |
5:56 |
7:43 |
7:8 |
C |
|||||||||||||
число |
|
|
1 |
|
X |
|
4 |
|
которых |
B |
7:56 |
6:09 |
6:81 |
4:49 |
7: |
2 |
4:6 |
5:47 |
C |
|||
предприятий |
для |
|
B |
C |
||||||||||||||||||
себестоимость |
· |
|
· |
|
|
|
|
B |
5:54 |
5:34 |
6:13 |
5:84 5:64 |
5:78 5:14 |
6:02 |
C |
|||||||
|
|
удовлетворяет |
B |
C |
||||||||||||||||||
неравенству |
|
|
|
|
|
. |
6). моду |
B |
6:12 |
5:42 |
4:58 |
6:85 |
5:15 |
4:47 |
5:56 |
4:89 |
C |
|||||
выборочного |
|
распределения. |
7). |
@ |
|
|
|
|
|
|
|
|
A |
|||||||||
коэффициент |
|
асимметрии. |
8). |
|
|
|
|
|
|
|
|
|
|
|||||||||
коэффициент эксцесса.
20.В целях изучения среднедушевого дохода семей в 2000 году была произведена 2% выборка из 17 тысяч семей. По результатам обследования среднедушевой доход семьи составил 20 тысяч рублей, со среднеквадратическим отклонением, равным 5 тысяч рублей.
Найти 97.5% доверительный интервал, покрывающий неизвестный генеральный среднедушевой доход, генеральная совокупность подчинена нормальному закону распределения.
21.При выборочном опросе 1300 телезрителей оказалось,что 300 из них предпочитают программы НТВ. Построить 90.% доверительный интервал, покрывающий генеральную долю числа зрителей, предпочитающих программы НТВ.
22.Для изучения демографических исследований обследовали 280 семей. Оказалось,что среди обследованных 38% составляют семьи из трех человек. Найти 99.% доверительный интервал для генеральной доли числа семей состоящей из трех человек.
18
23.Производится обследование на предмет среднего времени просмотра телепередач с 10 до 21 часов. Каким должен быть объем выборки, чтобы отклонение выборочной средней от генеральной не превышало 7 минут (по абсолютной величине) с вероятностью 0.975? Если в предыдущих исследованиях средне стандартное отклонение времени просмотра передач составило 38 минут.
24.При исследовании доходов населения города в 36000 чел., в случае бесповторной выборки для 1000 чел. получены распределения доходов.
xi |
2500 |
3000 |
3500 |
4000 |
4500 |
5000 |
5500 |
ni |
7 |
64 |
251 |
383 |
224 |
68 |
3 |
Найти границы среднего дохода с надежностью 99.%. Каким должен быть объем выборки,чтобы гарантировать те же границы с надежностью 0.9973?
25.Выборка из большой партии электроламп содержит 180 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1500 ч. Найти 92.5% доверительный интервал для средней продолжительности горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы равно 80 ч. Предполагается, что продолжительность горения ламп распределена по нормальному закону.
26.Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар будет замене сукразитом. Компания хотела бы быть уверенной, что не менее 70% ее потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 1200 человек, и 792 человека сказали, что новый напиток вкуснее старого. Может ли на уровне значимости 0.075 компания принять новый напиток в производство.
27.Некоторая компания, производящая средства для похудания, утверждает, что при приеме ее продукции в сочетании со специальной диетой позволяет сбросить в неделю, в среднем 400 грамм. Для проведения экспертизы случайным образом отобрано 45 человек. После проведения эксперимента обнаружено, что в среднем еженедельный сброс веса составил 340 грамм, исправленное среднеквадратическое отклонение составило 100 грамм. Проверить гипотезу от том, что средняя еженедельная потеря веса составляет 400 грамм. Принять уровень значимости равный 0.05.
28.Заключение страховых договоров в 140 филиалах страховых компаний составило 22000 штук в регионе А. В регионе В, в 190 филиалах составило 28000. Средне квадратические отклонения количества заключенных страховых полисов в регионах А и В, равны соответственно 20000 и 13500. Проверить на уровне значимости 0.05 существенно ли различаются регионы по количеству заключенных страховых договоров.
29.Доля убыточных предприятий в 2000 году в России в среднем составила 39%. В одном из регионов России 39%. В 2006 году в этой области было 9122 предприятий. На уровне значимости 0.01 и 0.0027 проверить, существенны ли различия в удельном весе убыточных предприятий в данном регионе по сравнению с общероссийским или нет.
30.Фирма посредник рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность заказа товара, при условии получения каталога, равна 0.09. Фирма разослала 1100 каталогов новой улучшенной формы и получила 120 заказов. На уровне доверия 97.5% и 99.% существенна ли новая форма каталога или нет.
31.Компания по производству зубной пасты утверждает, что новый вид пасты для детей лучше, чем другие пасты. Для проверки было отобрано 330 детей, пользующиеся новой пастой и 370 детей, пользующихся другими пастами для контрольной группы.
У37 детей из опытной группы были обнаружены новые признаки кариеса, у детей
из контрольной группы новые признаки кариеса обнаружены в 41 случаях. На уровне значимости 0.1 и 0.001 проверить обоснованность утверждений компании по производству
19
