- •МІністерство охорони здоров’я україни
- •Передмова
- •1. Функція
- •Способи задання функції
- •Класифікація функцій
- •Механічний та геометричний зміст похідної
- •Правило знаходження похідної
- •Приклади
- •Теореми
- •Приклади
- •Похідні вищих порядків
- •Приклади
- •Загальна схема дослідження функції та побудова графіка
- •Розв’язування
- •Графік заданої функції
- •3. Диференціал функції
- •Приклади
- •Розв’язування
- •Розв’язування
- •Невизначений інтеграл
- •Приклади
- •Властивості невизначеного інтегралу
- •Основна таблиця інтегралів
- •Методи інтегрування
- •Приклади
- •Інтегрування за частинами
- •Приклади
- •Визначений інтеграл
- •Задача про роботу змінної сили
- •Властивості визначеного інтегралу
- •Приклади
- •4. Диференціальні рівняння Диференціальні рівняння першого порядку
- •Диференціальні рівняння з відокремлюваними змінними
- •Приклади
- •Однорідні диференціальні рівняння
- •Приклади
- •Неоднорідне диференціальне рівняння
- •Розв’язок
- •Диференціальні рівняння вищих порядків. Основні означення і поняття
- •Приклади
- •5. Математична обробка результатів вимірювання. Обчислення похибок
- •Приклад:
- •Приклад:
Приклади
Знайти невизначений інтеграл функцій:
f(x) = 1
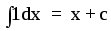
f(x) = ex
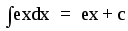
f(x) = sinx
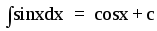
f(x) =
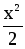
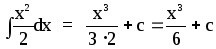
f(x) =
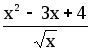
![]() ,
припустивши, щох
,
припустивши, щох![]() 0,
підінтегральну функцію можна записати
так:
0,
підінтегральну функцію можна записати
так: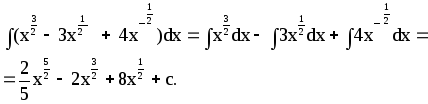
Властивості невизначеного інтегралу
Послідовне виконання операції диференціювання та інтегрування в будь-якому порядку з точністю до довільної сталої приводить до початкової функції d(
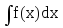 )=
f(x)dx
)=
f(x)dx = F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені.
= F(x)+c. Розглянуту властивість можна
сформулювати ще так: операції
диференціювання та інтегрування з
точністю до сталої є взаємно обернені.Якщо число а
 0,
то
0,
то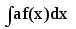 =a
=a .
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.
.
Дана властивість формулюється так:
сталий множник можна виносити за знак
невизначеного інтегралу.Невизначений інтеграл від суми (різниці) функції дорівнює сумі (різниці) невизначених інтегралів від кожної функції:
![]() .
.
Основна таблиця інтегралів
-
1.

2.
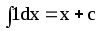
3.
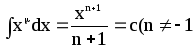
4.
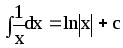
5.

6.
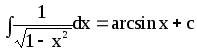
7.
 ;
;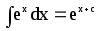
8.
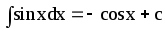
9.

10.
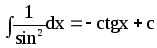
11.
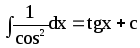
12.
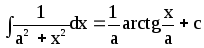
13.

14.

15.

16.
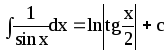
17.

18.

19.
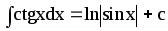
Методи інтегрування
Усі методи інтегрування функцій зводять невизначений інтеграл до інтегралу, який знаходиться в основній таблиці інтегралів або, як кажуть, до табличного інтегралу. Одним із найбільш сильних методів є так званий метод підстановки. В основі цього методу лежить заміна перемінної функції. Звернемо увагу читача на те, що заtтреба вибирати таку функціюt = w(x), щоб:
під інтегралом був явний диференціал від w(x)(w′(x)dx)або якщо даного диференціалу й немає, то його можна легко утворити за допомогою множення або ділення на стале число, відмінне від нуля;
інтеграл
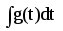 був
би табличним.
був
би табличним.
Якщо одночасно ці два пункти не виконуються, то інтеграл треба обчислювати іншими методами.
Приклади
Користуючись методом підстановки, обчислити невизначені інтеграли:
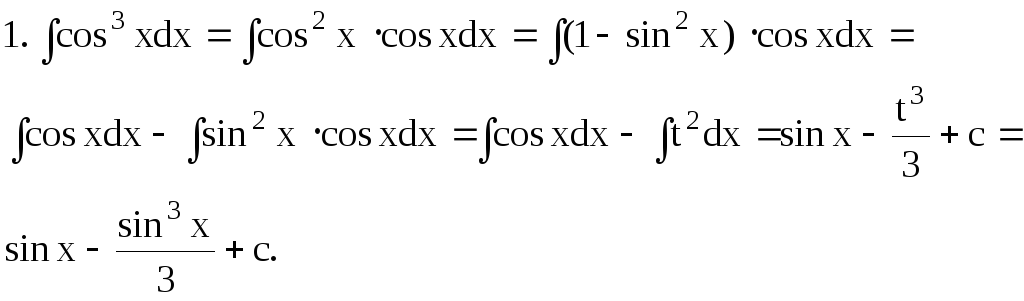
Підстановка: t = sinx; dt = cosxdx.
2.
![]()
Підстановка: t = lnx; dt =
![]() .
.
 .
.
Підстановка: t =x2; dt = 2xdx.
Підстановка: t = tg![]() .
.
Інтегрування за частинами
Розглянемо дві функції u =![]() (x),
v = g(x), які на деякому проміжку(а;b)є
неперервні і мають неперервні похідні
першого порядкуφ′(x),g′(x). Тоді
функціїuтаv мають диференціали
du = φ′(x)dx, dv = g′(x)dx, причому виконується
рівність d(uv) = udv+vdu. Візьмемо від обох
частин цієї рівності невизначений
інтеграл. Тоді внаслідок рівності
диференціалів невизначені інтеграли
відрізнятимуться тільки на сталу
величину. Отже, маємо рівність з точністю
до сталої
(x),
v = g(x), які на деякому проміжку(а;b)є
неперервні і мають неперервні похідні
першого порядкуφ′(x),g′(x). Тоді
функціїuтаv мають диференціали
du = φ′(x)dx, dv = g′(x)dx, причому виконується
рівність d(uv) = udv+vdu. Візьмемо від обох
частин цієї рівності невизначений
інтеграл. Тоді внаслідок рівності
диференціалів невизначені інтеграли
відрізнятимуться тільки на сталу
величину. Отже, маємо рівність з точністю
до сталої![]() =
=![]() –
–![]() але
але![]() =
=![]() .
Тому дістаємо формулу:
.
Тому дістаємо формулу:![]() =
uv –
=
uv –![]() .
Зазначимо, що у формулі ми не пишемо
сталої, адже стала міститься в інтегралі
.
Зазначимо, що у формулі ми не пишемо
сталої, адже стала міститься в інтегралі![]() ,
а сума двох сталих є сталою. Формула, що
написана, називаєтьсяформулоюінтегрування за частинами.
,
а сума двох сталих є сталою. Формула, що
написана, називаєтьсяформулоюінтегрування за частинами.
Приклади
Знайти невизначені інтеграли, користуючись методом інтегрування за частинами:
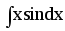 =
uv–
=
uv–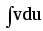 .
.
Введемо позначення u=x;dv=sinxdx.
Знаходимо![]() =
=![]() .v
= –cosx – сталої при знаходженніvне
пишемо. Сталу запишемо при обчисленні
інтегралу
.v
= –cosx – сталої при знаходженніvне
пишемо. Сталу запишемо при обчисленні
інтегралу![]() .
Оскількиuє відома функція: u = x, то
du = u′dx = dx. Отже,
.
Оскількиuє відома функція: u = x, то
du = u′dx = dx. Отже,![]() = –xcosx –
= –xcosx –![]() =
–xcosx+sinx+c. Якби ми взяли заu=sinx, то ми
приклад не розв’язали б.
=
–xcosx+sinx+c. Якби ми взяли заu=sinx, то ми
приклад не розв’язали б.
2.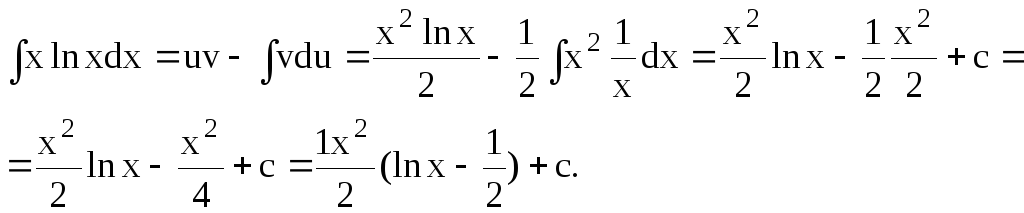
Введемо позначення: u =lnx ; du =
![]() ;
dv = xdx, v =
;
dv = xdx, v =![]() .
.
 .
.
Введемо позначення: u = ln2x; du = 2lnx![]() ;
dv =dx; dv =
;
dv =dx; dv =![]() .
.
Невизначений інтеграл
![]() будемо
інтегрувати за частинами.
будемо
інтегрувати за частинами.
Нехай u = lnx; dv = dx. Тоді du =![]() dx, v =
dx, v =![]() =
x.
=
x.
Отже,
![]() xlnx –
xlnx –![]() =
xlnx – x + с.
=
xlnx – x + с.
Остаточно знаходимо
![]() =
xln2x –2(xlnx – x) + c.
=
xln2x –2(xlnx – x) + c.
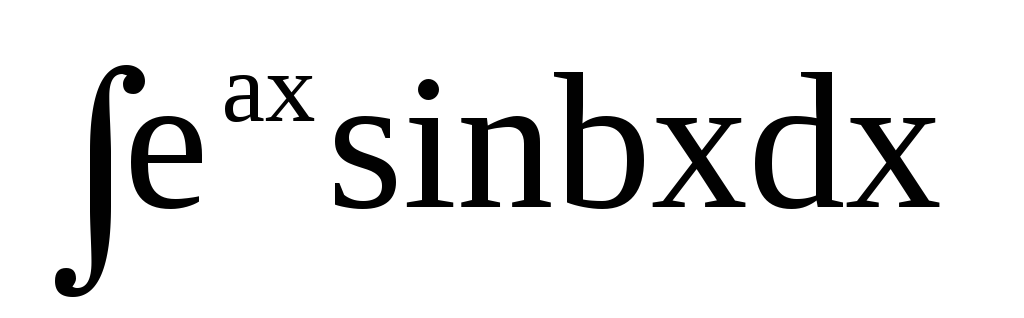 =
еах
=
еах
Позначимо в цьому інтегралі u = eax , dv = sinbxdx. Звідки du = aeaxdx,
v =
![]() = –
= –![]() .
.
Тоді
![]() .
.
Інтеграл у правій частині цієї рівності
теж обчислюється за частинами. Введемо
позначення: u = eax; dv = cos bxdx,
звідки du = eaxdx v =![]() =
=![]() =
=![]() .
Скориставшись формулою метода інтегрування
за частинами, маємо
.
Скориставшись формулою метода інтегрування
за частинами, маємо![]() .
.
Підставивши значення цього інтегралу в рівність, дістанемо:
![]() .
.
У правій частині цієї рівності маємо той самий інтеграл, що у лівій. Тому, розв’язуючи цю рівність відносно інтегралу, знаходимо:
![]() .
.