Зміст

Вступ 5

1.Основні означення та властивості 6

2.Теорема Джексона. 15

3.Узагальнення теореми Джексона. 18

4.Теорема С. Н. Бернштейна. 22

5.Теорема про рівність класу Ліпшиця і класу Діціана і Тотіка. 28

Висновок 32

Список використаної літератури 33

Вступ

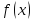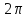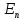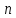Нехай – неперервна, – періодична функція, а– її найкраще наближення тригонометричними поліномами не вище-го порядку. В силу другої теореми Вейєрштраса виявляється, що

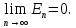
Чим «простіше» буде наближення функції 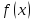, тим точніше вона буде представлятися тригонометричним поліномом. Інакше кажучи, для більш простіших функцій,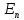повинно прямувати до нуля швидше, ніж для функцій складної природи. В дипломній роботі буде розглядатися питання, як впливає покращення структурних властивостей функції, що наближається, на порядок спадання її найкращого наближення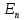. Ці результати, головним чином, належать Джексону.

Теорема Джексона дає оцінку зверху для найкращого наближення функції многочленами або періодичної функції тригонометричними поліномами. Теорема дає можливість досліджувати властивості найкращих наближень в залежності від диференційованих властивостей функції.

Зручною характеристикою структурних властивостей функції є величина, яка називається «модулем неперервності» цієї функції. У роботі вивчаються властивості звичайного модуля неперервності і властивості введені Діціаном і Тотіка, і на їх базі досліджується поведінка найкращих наближень неперервної функції алгебраїчними многочленами.

В дипломній роботі будуть згадані деякі результати С. Н. Бернштейна, обмежуючись, розглядом неперервних, 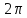– періодичних функцій. С.Н.Бернштейну належить ряд важливих результатів, де він вирішує обернену задачу: задачу характеристики структурно-диференційовних властивостей функції на основі порядку малості її найкращого наближення. В цілому всі ці дослідження дають класифікацію неперервних функцій за порядками їх найкращих наближень.

1. Основні означення та властивості

Означення 1.1. Нехай на проміжку 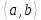задана функція . Візьмемо будь-яке додатне число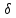і розглянемо всі пари чисел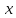і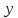, які належать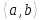і задовольняють наступну нерівність

Точна верхня межа чисел

називається модулем неперервності функції .

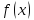Властивості модуля неперервності.

1. Функція 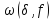монотонно зростає. Дійсно, якщо 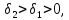то множина пар 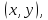які задовольняють умову 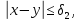ширше, ніж множина таких пар, для яких . Зважаючи на те, що при розширенні числової множини її точна верхня межа може хіба лише збільшитись, ясно те, що

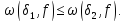
2. Для того, щоб функція 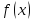була рівномірно неперервна на проміжку 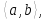необхідно та достатньо, щоб

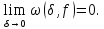
3. Якщо 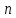– натуральне число, то

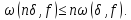
Дійсно, нехай

Розіб’ємо сегмент 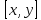на 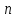рівних частин точками

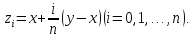
Очевидно, що

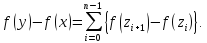
З іншого боку, 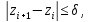звідки

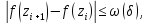
і тому

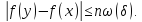
Властивість доведена.

4. При будь-якому додатному

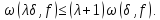
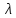Дійсно, нехай є ціла частина, така що. Тоді

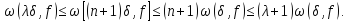
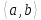Означення 1.2. Якщо функція задана на проміжку і при всіхі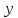 із цього проміжку задовольняє нерівність

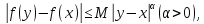
то кажуть, що функція задовольняєумову Ліпшиця з показником 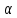і коефіцієнтом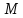, і пишуть

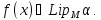
Інакше кажучи, 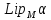є клас всіх функцій, які задовольняють умову Ліпшиця даного порядку 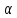із заданим коефіцієнтом, а є класом функцій, які задовольняють умові Ліпшиця порядку 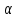з будь-яким коефіцієнтом.

Означення 1.3. Найкраще наближення. Для будь-якої обмеженої вимірної функції 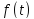, заданої на кінцевому відрізку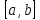, і будь-якого натурального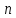існує звичайний многочлен

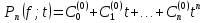
степеня не вище 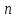, що найменш ухиляється від неї на цьому відрізку, тобто такий, що серед усіх інших многочленів, які мають степінь, не більше ніж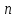, реалізує найменше значення для відхилення

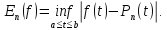
Означення 1.4. Нехай функція 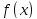належить, тобто неперервна і має період 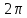. Взявши будь-який тригонометричний поліном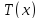порядку не вище 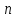, покладемо

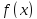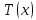Будемо називати цю величину відхиленням полінома від функції. Змушуючи поліномпробігати всю множину^ ми отримаємо цілу множину невід’ємних відхилень 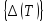. Точна нижня межа

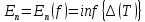
цієї множини називається найменшим відхиленням поліномів із 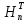від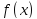абонайкращим наближенням до 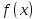поліномами із.

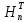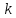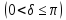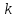Означення 1.5. Нехай – натуральне число. Будемо казати, що функція є модуль неперервності -го порядкуфункції 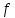, якщо

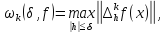
де 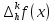– кінцева різниця функції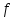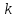-го порядку з шагом: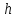

Властивості модуля неперервності 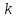-го порядку.

Лема 1.1. Для будь-якого натурального 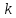і будь - якого

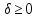
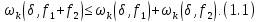
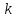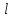Лема 1.2. Нехай і – натуральні числа, 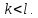Тоді для будь-якого

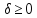
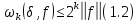
і

Доведення. Покладемо

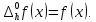
Тоді для 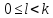маємо

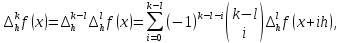
звідки

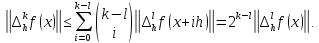
Звідси при 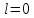випливає (1.2), а при 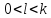– (1.3).

Вважаючи в (1.3) 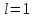, знаходимо, що

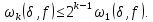
Із останньої нерівності видно, що для будь-якого натурального

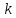
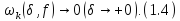
Лема 1.3. Для будь-якого натурального модуль неперервності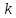-того порядкує неперервною функцією від.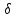

Доведення. Нехай 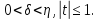Маємо

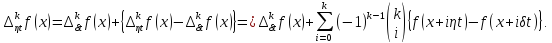
Звідси

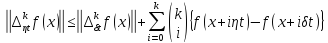
і

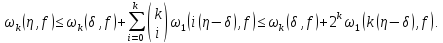
Таким чином,

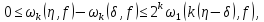
і так як при 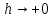, то звідси випливає неперервність функції 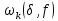, і лема доведена.

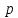Лема 1.4. Нехай і– натуральні числа. Тоді для будь-якого

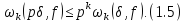
Доведення. Індукція по 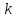дає формулу

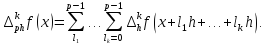
Звідси

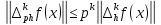
і

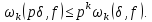
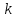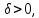
Лема 1.5. Нехай – натуральне число 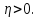Тоді

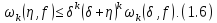
Якщо, крім тог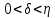о, , то

Доведення. Доведемо спочатку нерівність (1.6). Ця нерівність очевидна для 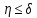. Розглянемо 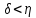. Знайдемо натуральне число 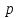із умов

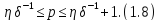
Тоді , і так як 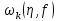є не спадаючою функцією від , то, приймаючи до уваги (1.5) і (1.8), отримаємо

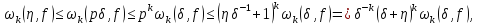
і нерівність (1.6) доведена.

Нерівність (1.7) випливає із (1.6), так як 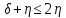для

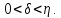
Нерівність (1.7) показує, що для будь-якого 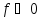і будь-якого натурального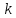

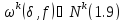
Лема 1.6. Нехай 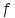має-ту похідну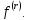Тоді

і для будь-якого натурального

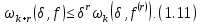
Доведення. Обидві нерівності безпосередньо випливають із формули

Означення 1.6. Нехай . Тодімодуль неперервності

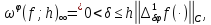
де

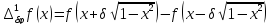
Означення 1.7. Нехай – клас функцій, що визначені на сегменті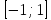і задовольняють умову Діціана і Тотіка

Теорема 1.1. Діціана і Тотіка.[3]. Для того, щоб необхідно і достатньо, щоб