2. Теорема Джексона.

Фундаментальне значення для конструктивної теорії функцій мало відкриття Джексоном можливості суттєвого уточнення класичної теореми Вейєрштраса і нове формулювання її у вигляді нерівності.

Теорема 2.1. Для будь-якої функції 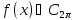справедлива оцінка

Доведення. Для доведення скористаємося наступною теоремою.

Теорема 2.2. Нехай функція 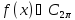і має модуль неперервності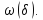Покладемо

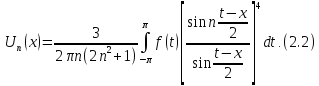
Тоді при всіх 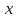справедлива оцінка

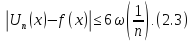
Але так як 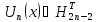, то тим більше

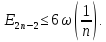
Якщо 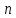– парне натуральне числ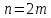о,, то

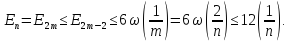
Якщо ж 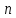число непарне,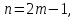то

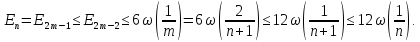
Отже, оцінка (1) справедлива для будь-якого натурального

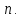
Зважаючи на те, що для будь якої функції із

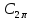
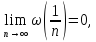
зрозуміло, що доведена теорема Джексона містить у собі другу теорему Вейєрштраса.

Наслідок 2.1. Якщо

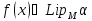
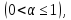
В свою чергу звідси маємо

Наслідок 2.2. Якщо у 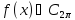існує обмежена похідн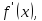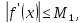о то

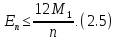
Дійсно, за цих умов

3. Узагальнення теореми Джексона.

У 1950 році С. Б. Стечкіним була опублікована стаття, у якій один із параграфів присвяченій узагальненню теореми Джексона. Як відомо, Джексон довів наступну теорему: якщо 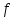має неперервну 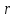-у похідну 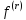, то

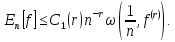
Таким чином, теорема Джексона дає оцінку зверху для найкращих наближень, якщо відомі диференційовані властивості функції, що апроксимується.

В 1947 році з’явилася робота С. Н. Бернштейна. Одна із теорем цієї роботи містить у якості наслідку таку пропозицію: нехай

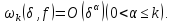
Тоді

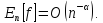
С. Б. Стечкіним доведено наступне узагальнення цих теорем:

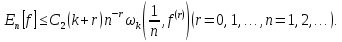
Було отримано невелике посилення теореми Джексона о найкращих наближеннях періодичних функцій тригонометричними поліномами.

Лема 3.1. Нехай дано натуральне число 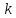. Існує послідовність ядер 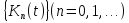, де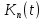є тригонометричний поліном порядку не вище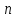, який задовольняє умови:

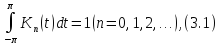
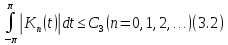
і

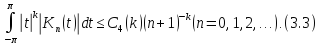
У якості ядер 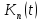можна взяти ядра Джексона достатньо високої степені, тобто покласти

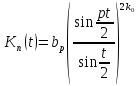
де 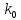– ціле, не залежить від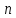,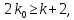натуральне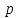визначається із нерівності

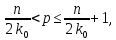
а 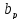обирається так, щоб виконувалось нормування (1).

Лема 3.2. Якщо послідовність ядер 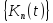задовольняє усім умовам попередньої леми, то

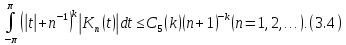
Доведення. Користуючись (3.2) і (3.3) маємо наступне

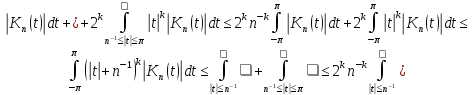
і лема доведена.

Теорема 3.1. Нехай

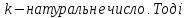
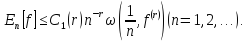(3.5)

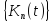
Доведення. Нехай послідовність ядер 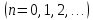задовольняє всі умови леми 1. Покладемо

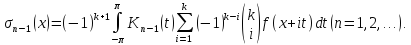
Видно, що 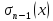є тригонометричний поліном порядку не вище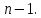Оцінимо . Маємо

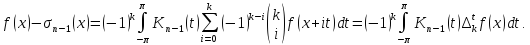
Тому

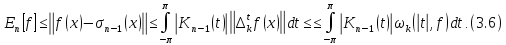
Оцінимо останній інтеграл. Вважаючи в нерівності (1.6) 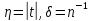, отримаємо, що

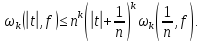
Звідси і із (3.4) слідує:

Підставивши цю оцінку в (3.6), отримаємо твердження теореми.

Наслідок. Нехай 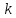– натуральне число,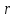– ціле невід’ємне. Тоді

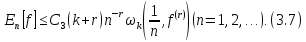
Дійсно, згідно (1.11),

Використання теореми 3.1 дає (3.7).

4. Теорема с. Н. Бернштейна.

Теорема 4.1. Нехай 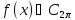і – її найкраще наближення поліномами із 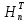. Якщо при всіх натуральних

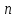
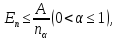
тоді при 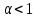можна стверджувати, що

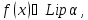
А якщ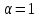о , то

^.

Доведення. Для будь-якого натурального 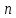існує тригонометричний поліном 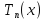порядку не вище 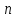, для якого

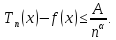
Покладемо

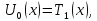
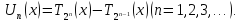
Легко побачити, що

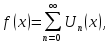
або

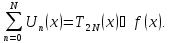
Візьмемо будь-яке число 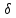, для якого

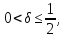
і нехай 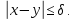Тоді

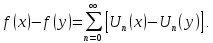
Нехай натуральне число 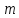підібрано із умови

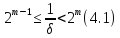
(очевидно, 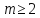). В такому разі

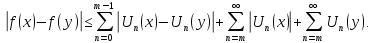
Дамо оцінку поліному

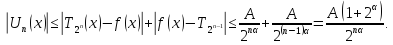
Звідси

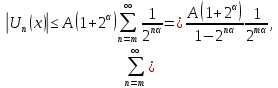
отже,

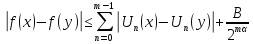
де покладемо для кратності

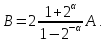
З іншого боку, є тригонометричний поліном порядку не вище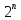. Отже, для його похідної на основі нерівності С. Н. Бернштейна^ справедлива оцінка

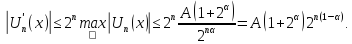
На основі формули Лагранжа

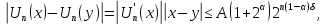
Тому

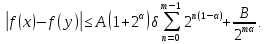
Зважаючи на те що 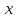і 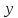об’єднані єдиною умовою 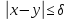, остання нерівність показує, що

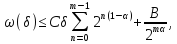
де 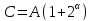. Помітно, що, в силу (4.1)

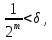
надамо останній нерівності вигляд

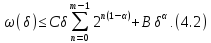
До цих пір міркування однаково відносились як до випадку, коли 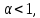так і до того, коли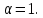Тепер нам треба розрізнити ці випадки.

Якщо то

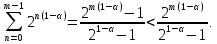
Але за (4.1)

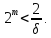
Отже,

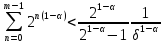
і

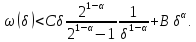
Інакше кажучи,

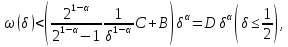
А це означає, що .

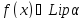Якщо ж 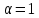, то нерівність (4.2) має вигляд

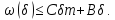
Із нерівності 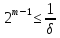випливає, що

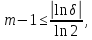
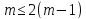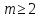а так як (або), то

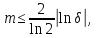
звідки

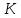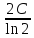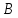Позначимо через число, більше, ніж і , знаходимо

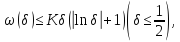
Що і завершує доведення теореми.