
- •Структура модели химико-технологических систем непрерывного действия
- •1.1. Общая характеристика
- •Модели технологических аппаратов
- •Модели структуры химико-технологических систем
- •2. Анализ статических режимов
- •2.1. Структурный анализ разомкнутых систем
- •2.2. Структурный анализ систем с рециклами
- •3. Динамические модели
- •3.1. Способы описания динамики химико-технологичсеких систем
- •3.2. Формирование моделей динамики систем из моделей аппаратов
- •4. Методы решения систем уравнений математической модели
- •4.1. Методы решения систем алгебраических уравнений
- •4.2. Методы решения совместных систем конечных и дифференциальных уравнений
- •5. Моделирование стохастических систем
- •6. Системы непрерывного моделирования
- •Литература
- •Часть 2. Математическое моделирование химико-технологических систем непрерывного действия
- •125047 Москва, Миусская пл., д.9
3. Динамические модели
3.1. Способы описания динамики химико-технологичсеких систем
Назначение моделирования динамики ХТС — определение закономерности изменения выходов при изменении входов как функций времени. Моделирование динамики ХТС выполняется с различными целями (см. раздел “Цели моделирования” в части 1 настоящего пособия), но, в основном, - с целью синтеза систем автоматического управления.
Динамические свойства ХТС можно описывать различными моделями, например, в виде уравнений, связывающих выходы системы с ее входами; уравнений в пространстве состояний, уравнений движения в фазовом пространстве, а для линейных систем — в виде передаточных матриц. Рассмотрим наиболее распространенные способы описания динамики ХТС.

Простейшим
примером одномерной системы может
служить изотермический РИС, в котором
протекает простая необратимая реакция
 при изменяющейся концентрации реагента
A на входесвх(t).
Моделью этого реактора, если выразить
скорость реакции через концентрацию
реагента, является линейное неоднородное
дифференциальное уравнение первого
порядка, выражающее материальный баланс
по компоненту A в нестационарных условиях:
при изменяющейся концентрации реагента
A на входесвх(t).
Моделью этого реактора, если выразить
скорость реакции через концентрацию
реагента, является линейное неоднородное
дифференциальное уравнение первого
порядка, выражающее материальный баланс
по компоненту A в нестационарных условиях:
 (4)
(4)
Уравнение (4) связывает выход с(t) с входом свх(t) как функцию времени. В момент времени t0=0 реактор находится в некотором состоянии с(0)=с0.
В общем случае модель одномерной линейной системы есть скалярное уравнение вида:
 (5)
(5)
при начальном условии: y(0)=y0 , где a,b – коэффициенты.
Обычно ХТС описывается системой n обыкновенных уравнений первого порядка, так как имеет векторные: вход X(t) = {x1(t),x2(t),...,xm(t)} и выход Y(t)={y1(t),y2(t),...,yn(t)}, где m — размерность входа; n — размерность выхода (рис.18).

или - в векторной форме записи:

где
A=aijnn;
B=bijnm
—
матрицы коэффициентов.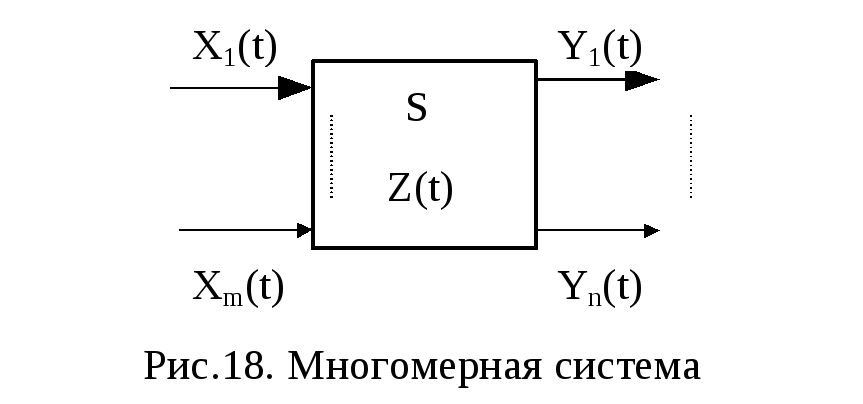
В
качестве примера линейной динамической
многомерной системы можно рассмотреть
РИС, в котором происходят последовательные
реакции
 ,
при изменении концентрациисAвх(t)
реагента A на входе.
,
при изменении концентрациисAвх(t)
реагента A на входе.

Система имеет один вход сAвх(t) и два выхода сA(t), сP(t).
Обычно ХТС — это нелинейные объекты; поэтому их модели имеют вид систем нелинейных дифференциальных уравнений.
Рассмотрим,
например, изотермический РИС, в котором
протекает реакция
 ;
пусть на входе независимо меняются
концентрацииcAвх(t)
и
cBвх(t);
тогда система уравнений модели будет
иметь вид:
;
пусть на входе независимо меняются
концентрацииcAвх(t)
и
cBвх(t);
тогда система уравнений модели будет
иметь вид:

Система имеет два входа cAвх(t), cBвх(t) и два выхода cА(t), cB(t). Нелинейность обусловлена наличием нелинейного кинетического члена и ненулевыми начальными условиями.
Размерность системы определяется числом k переменных состояния Z(t)={z1(t),z2(t),...,zk(t)}. Число выходов не зависит от числа переменных состояния и определяется целью исследования. Выходы линейной системы представляются линейной комбинацией переменных состояния и входов:

или в матричной форме
 ,
,
где C — матрица размерности kn; D — матрица размерности km.
Другой способ описания динамики — ее описание в пространстве состояний, то есть в виде

Наличие функциональной связи между состоянием системы и ее выходом позволяет осуществить переход от модели динамики в виде “вход-выход” к ее модели в пространстве состояний. Для перехода от формы уравнений, связывающих выход со входом, необходимо произвести замену функциональных операторов Ay(t) на Az(t). Наиболее просто эта замена производится, когда в правой части исходных уравнений модели не содержатся производные от внешних воздействий на систему, то есть уравнения имеют вид:

Составим
уравнения в переменных состояния для
РИС, в котором проводится реакция
 .
.

или в более привычной форме:

Обозначим  тогда
тогда
 ,
то есть
,
то есть

или - в векторной форме записи:

Сложнее происходит преобразование, когда правая часть исходных уравнений содержит производные.
Найдем уравнение состояния системы, описываемой дифференциальным уравнением:
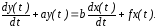
Введем переменную состояния z1(t) так, чтобы:

Продифференцируем
 и подставим значение
и подставим значение

Разрешим исходное дифференциальное уравнение относительно производной

Сравнивая коэффициенты при одинаковых производных, получим: 0=b; 1=f.
Тогда:

Распространен также метод описания динамики систем в фазовом пространстве, в котором в качестве координат используются пространственные координаты и импульсы. Мгновенное состояние системы в фазовом пространстве изображается точкой, которая называется изображающей точкой. Изображающая точка в фазовом пространстве движется по кривой, называемой фазовой траекторией. Задание уравнений движения в фазовом пространстве часто оказывается удобным, так как просматривается непосредственная связь процесса движения с энергией систем.
Если система представляет собой объект с распределенными параметрами, то ее моделью является совместная система дифференциальных уравнений с частными производными и алгебраических уравнений.
Наиболее характерным примером является динамическая модель РИВ, содержащая уравнения материального и теплового балансов, а также уравнения физико-химических законов (действующих масс и Аррениуса).
Общий материальный баланс РИВ в динамике имеет вид следующего дифференциального уравнения:
 (6)
(6)
то есть аккумуляция массы в реакторе равна разности масс, входящих в реактор реагентов и выходящих из него продуктов. Выделим произвольное сечение x в реакторе и зададим приращение x. Тогда:

где
 — линейная скорость потока, мч-1;
— линейная скорость потока, мч-1;

 —плотность
массы потока, кгм-3;
—плотность
массы потока, кгм-3;
 —площадь
поперечного сечения реактора, м2.
—площадь
поперечного сечения реактора, м2.
Тогда m имеет размерность массового расхода (кгч-1), а M — размерность массы (кг).
Подставив выражение mвх, mвых и M в уравнение (6), тогда получим:
![]() .
.
Так как F=const, то, вынеся F за знак производной и сократив на F, получим

Разделим обе части на x

Перейдем
к пределу при x0;
тогда в правой части уравнения получим
производную
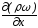 со знаком минус (по определению
производной). Таким образом, уравнение
общего материального баланса имеет вид
уравнения:
со знаком минус (по определению
производной). Таким образом, уравнение
общего материального баланса имеет вид
уравнения:
 ,
,
для которого должны быть заданы начальное и граничное условия.
Составим теперь материальный баланс по произвольному компоненту k, обозначив c(x,t) концентрацию в сечении x в момент времени t.

Сократив F и разделив обе части на x, получим:
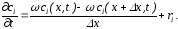
При
x0 
при граничном условии ci(0,t)=ci вх(t)
и начальном условии ci(x,0)=ci0(x).
Модель реактора с продольным перемешиванием диффузионного типа по аналогии будет иметь вид:

при граничных условиях:


Вывод аналогичен выводу уравнений баланса для РИВ.
Методы исследования динамики хорошо разработаны только для линейных систем, то есть для таких, для которых справедлив принцип суперпозиции

при любых n,c1,...,cn; x1(t),...,xn(t) , где A — функциональный оператор. Выражение, приведенное выше, означает, что воздействие оператора A на сумму функций xi(t) равно сумме воздействий оператора A на функции xi(t).
Для линейных систем справедливо выражение, называемое интегралом суперпозиции:

Выражение (t,) называется переходной матрицей (фундаментальной матрицей, характеристической матрицей или матрицантом). В скалярном случае (t,) называется переходной (характеристической) функцией линейной системы. Элемент ij(t,) переходной матрицы моделирует переходный процесс по i переменной состояния Zi(t) от единичного начального условия по j переменной состояния Zj(t0)=1 при нулевых начальных условиях по остальным переменным состояния. Интеграл суперпозиции моделирует реакцию Z(t) на входной сигнал f(t) системы, описываемой уравнением состояния:
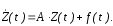
Таким образом, реакция линейной системы на любые входные возмущения при любых начальных условиях может быть определена следующим выражением:
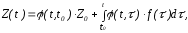
а автономной системы, то есть не испытывающей внешнего воздействия, - выражением:
 .
.
Интеграл суперпозиции справедлив для неавтономной (открытой) системы при нулевых начальных условиях (Z0=0).
Динамическая модель системы порядка n имеет вид неоднородного векторного уравнения с ненулевыми начальными условиями:

Ее решение ищется в виде суммы:

где Zp(t) — частное решение неоднородного уравнение; Za(t) — дополняющее (общее или свободное) решение однородного уравнения:

Неоднородная система уравнений может быть решена, например, методом вариации параметров [5].
Динамическую модель ХТС можно представить в виде функционального оператора , который ставит в соответствие множеству функций входа x1(t), x2(t), ..., xm(t) множество функций выхода y1(t), y2(t), ..., yn(t). Например, интегральный оператор ставит в соответствие каждой функции x(t) функцию y(t) согласно следующему правилу:
 (7)
(7)
где функция Q(t,), называемая ядром функционала, является характеристикой моделируемого объекта. Функция Q(t,) получается в результате действия оператора А на функцию P(t,).
Смысл принципа суперпозиции состоит в том, что, зная реакцию линейной системы на произвольное стандартное возмущение P(t,), можно определить ее реакцию на входное возмущение произвольного вида x(t), для чего достаточно представить его в виде интеграла (7), что достигается подбором S().
В качестве функции P(t,) выбираются стандартные функции, наиболее просто реализуемые экспериментально: -функция (функция Дирака*), h-функция (функция Хевисайда*), воздействие гармонического вида.
Реакция Q(t,) линейной системы на стандартное возмущение P(t,) характеризует динамические свойства системы и называется характеристической функцией. Вид характеристической функции зависит от вида стандартного возмущения. Реакция системы на -функцию называется весовой или импульсной переходной функцией; на h-функцию — переходной функцией; на возмущение гармонического вида — частотной характеристикой. Подробно анализ динамических свойств линейных систем изложен в [6].
Так как принцип суперпозиции справедлив только для линейных систем, а ХТС, как правило, нелинейны, то необходимо выполнить линеаризацию исходных нелинейных операторов, то есть их замену линейными операторами. Нелинейность функциональных операторов может быть обусловлена либо ненулевыми начальными условиями, либо содержанием неизвестных функций в степени, отличной от единицы. Если нелинейность обусловлена ненулевыми начальными условиями, то линеаризация состоит в их замене нулевыми начальными условиями; если нелинейность обусловлена наличием нелинейных зависимостей между переменными, то необходимо заменить нелинейный оператор эквивалентным линейным.
Линеаризация
нелинейного оператора
 – процедура его замены эквивалентным
линейным оператором
– процедура его замены эквивалентным
линейным оператором в
том смысле, что каждая функция выхода
в
том смысле, что каждая функция выхода
 оператора
оператора с помощью точного соотношения выражается
через соответствующую выходную функцию
линейного оператора
с помощью точного соотношения выражается
через соответствующую выходную функцию
линейного оператора .
Любой оператор
.
Любой оператор ,
задаваемый линейными дифференциальными
уравнениями с ненулевыми начальными
условиями можно свести к линейному
оператору
,
задаваемый линейными дифференциальными
уравнениями с ненулевыми начальными
условиями можно свести к линейному
оператору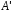 ,
задаваемому теми же самыми уравнениями,
но с нулевыми начальными условиями
,
задаваемому теми же самыми уравнениями,
но с нулевыми начальными условиями

где
 - вектор-функция входа;
- вектор-функция входа;
 - вектор-функция выхода;
- вектор-функция выхода;
 - нелинейная функция, являющаяся
результатом воздействия оператора
- нелинейная функция, являющаяся
результатом воздействия оператора
 на нулевой вход. В качестве примера
рассмотрим РИС, в котором в изотермических
условиях протекает простая реакция
на нулевой вход. В качестве примера
рассмотрим РИС, в котором в изотермических
условиях протекает простая реакция .
Оператор
.
Оператор имеет вид дифференциального уравнения
имеет вид дифференциального уравнения
 ,
,
но
оператор
 нелинеен, так как
нелинеен, так как (не выполняется принцип суперпозиции).
(не выполняется принцип суперпозиции).
Сведем
оператор
 к эквивалентному линейному. Для этого
введем функцию, которая является решением
уравнения
к эквивалентному линейному. Для этого
введем функцию, которая является решением
уравнения
 .
.
Решение
уравнения имеет вид
 и представляет результат действия
нелинейного оператора
и представляет результат действия
нелинейного оператора на нулевой вход
на нулевой вход .
Введем теперь линейный оператор
.
Введем теперь линейный оператор ,
задаваемый уравнением:
,
задаваемый уравнением:
 где
где
 ,
,
а
функция
 выражается
через функцию
выражается
через функцию следующим образом
следующим образом
 .
.
Таким
образом, исходный нелинейный оператор
 заменен линейным оператором
заменен линейным оператором .
.
Если
оператор
 имеет вид нелинейного дифференциального
уравнения, то невозможно точно выразить
его выходную функцию через входную
функцию линейного оператора, возможна
только некоторая аппроксимация
нелинейного оператора
имеет вид нелинейного дифференциального
уравнения, то невозможно точно выразить
его выходную функцию через входную
функцию линейного оператора, возможна
только некоторая аппроксимация
нелинейного оператора ,
которая для систем непрерывного действия
выполнима ввиду незначительности
отклонений параметров входа
,
которая для систем непрерывного действия
выполнима ввиду незначительности
отклонений параметров входа и выхода
и выхода от их стационарных значений
от их стационарных значений и
и .
Введем функции
.
Введем функции и
и , то есть заменим исходный нелинейный
оператор
, то есть заменим исходный нелинейный
оператор эквивалентным ему нелинейным оператором
эквивалентным ему нелинейным оператором ,
преобразующим входную функцию
,
преобразующим входную функцию в выходную функцию
в выходную функцию .
Оператор
.
Оператор может быть заменен линейным оператором
может быть заменен линейным оператором ,
что эквивалентно разложению функции
правой части дифференциального уравнения
в ряд Тейлора в окрестности стационарной
точки с удержанием линейных членов
разложения.
,
что эквивалентно разложению функции
правой части дифференциального уравнения
в ряд Тейлора в окрестности стационарной
точки с удержанием линейных членов
разложения.
Пусть исходное нелинейное дифференциальное уравнение, являющееся динамической моделью объекта, имеет вид

Тогда
стационарное значение
 может быть найдено в результате решения
нелинейного алгебраического уравнения
может быть найдено в результате решения
нелинейного алгебраического уравнения

Разложение
функции
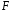 в окрестности точки (
в окрестности точки ( ,
, )
по степеням отклонения переменных
)
по степеням отклонения переменных
 от их стационарных значений имеет вид
от их стационарных значений имеет вид
 ,
,
где индекс 0 при производных обозначает их значения в стационарной точке.
Ввиду
малости
 ,
,
 по сравнению с
по сравнению с
 ,
,
 можно заменить исходное нелинейное
дифференциальное уравнение линейным
можно заменить исходное нелинейное
дифференциальное уравнение линейным

с
начальным условием
 и, следовательно:
и, следовательно:
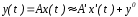 ,
,
где
 - входная вектор-функция оператора
- входная вектор-функция оператора ,
,
 - значение выхода в стационарном режиме.
- значение выхода в стационарном режиме.
Рассмотрим
в качестве примера РИС, в котором
протекает простая реакция
 в изотермическом режиме. Динамическая
модель реактора имеет вид нелинейного
дифференциального уравнения
в изотермическом режиме. Динамическая
модель реактора имеет вид нелинейного
дифференциального уравнения

с
начальным условием
 .
.
Определим
значение
 в
стационарном режиме из уравнения
в
стационарном режиме из уравнения
 ,
,
решение которого имеет вид
 .
.
Физический смысл имеет решение со знаком “+“ в числителе.
Тогда линейное дифференциальное уравнение, заменяющее исходное нелинейное будет иметь вид
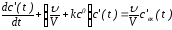
при
начальном условии
 то
есть исходный нелинейный оператор
то
есть исходный нелинейный оператор
 заменен линейным
заменен линейным .
.
Если коэффициенты модели не зависят от времени, то не зависит от времени реакция системы на идентичные входные возмущения. Такие динамические системы называются стационарными. Их динамическими моделями являются однородные функциональные операторы. В общем виде свойства стационарности функционального оператора можно представить как результат воздействия на входную функцию x(t) оператора сдвига, который смещает входную функцию x(t) на время , не изменяя ее.
Одним
из часто применяющихся способов описания
динамических свойств стационарных
линейных объектов является их представление
в виде передаточных функций.
Передаточной
функцией
 называется
отношение преобразованных по Лапласу*выхода к входу при ступенчатом единичном
входном возмущении.
называется
отношение преобразованных по Лапласу*выхода к входу при ступенчатом единичном
входном возмущении.
Преобразованием Лапласа функции f(t), удовлетворяющей условию Дирихле (функция f(t) ограничена, кусочно-монотонна и имеет конечное число точек разрыва первого рода), называется функция F(p), определяемая следующим образом:

Функция
 комплексного переменного называется
изображением функцииf(t),
которая в этом случае называется
оригиналом.
Для перехода из пространства изображений
в пространство оригиналов применяется
обратное
преобразование Лапласа (интеграл
Лапласа – Меллина):
комплексного переменного называется
изображением функцииf(t),
которая в этом случае называется
оригиналом.
Для перехода из пространства изображений
в пространство оригиналов применяется
обратное
преобразование Лапласа (интеграл
Лапласа – Меллина):

где
i
— мнимая единица, а значение выбирается
таким образом, чтобы все особые точки
функции
 лежали бы левее прямой Rep=, гдеRep
– действительная часть комплексной
переменной p.
лежали бы левее прямой Rep=, гдеRep
– действительная часть комплексной
переменной p.
Например, динамическая модель РИС имеет вид дифференциального уравнения:

В частном случае начальные условия могут быть нулевыми с(0)=0.
Преобразуем дифференциальное уравнение по Лапласу; тогда получим линейное алгебраическое уравнение:

Решим
его относительно неизвестной функции
 ,
тогда получим
,
тогда получим

где
 ,
,
 — соответственно преобразованные по
Лапласу концентрации реагента А на
входе и выходе реактора.
— соответственно преобразованные по
Лапласу концентрации реагента А на
входе и выходе реактора.
Таким образом, РИС представляет апериодическое звено первого порядка.
Для
получения решения в пространстве
оригиналов, то есть во временной области,
следует применить к
 обратное преобразование Лапласа
обратное преобразование Лапласа
 .
.
Тогда при нулевых начальных условиях получим
 .
.
Следовательно, концентрация c(t) на выходе реактора при ненулевых начальных условиях c(0)=c0 определяется выражением
 ,
,
представляющим общее решение линейного неоднородного уравнения динамики РИС.
