МАТЕМАТИКА 1 СЕМЕСТР АНАЛИЗ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

то предел отношения двух бесконечно малых функций может быть любым; его

называют неопределенностью вида 0 . Отыскание предела в случае неопреде-

0

ленности называют раскрытием неопределенности.

Пример 3.2. Найти lim	x3 4x 3	.
x 1	x2 6x 5

Решение. Числитель и знаменатель дроби при x 1 обращаются в ноль, поэтому

имеем неопределенность вида 0 . Для ее раскрытия числитель и знаменатель

0

разложим на множители, причем один из множителей уже известен – это (x 1) . Поделив на него многочлен, стоящий в числителе, получим и другой множитель.

Итак,

lim

x3 4x 3

0

lim

(x 1) (x2 x 3)

lim

x2

x 3

1

1

.

2

6x 5

(x 1) (x 5)

x 5

4

4

x 1 x

0

x 1

x 1

1

.

Пример 3.3.

Найти

lim

1 x

x

x 0

Решение. Имеем неопределенность вида 0 . Для ее раскрытия умножим чис-

0

литель и знаменатель на (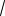1 x 1) :

lim

1 x 1

=

0

= lim

( 1 x 1) ( 1 x 1)

= lim

(1 x) 1

lim

1

1

.

x

0

2

x ( 1 x 1)

1 x 1)

1 x 1

x 0

x 0

x 0 x (

x 0

3.3. Первый замечательный предел

При вычислении пределов выражений, содержащих тригонометрические

функции, часто используется lim	sin x		. Он является неопределенностью					0	. По-
x 0	x						0
кажем, что
			lim	sin x	1	.			(3.1)
				x
			x 0

Это равенство называют первым замечательным пределом.

Докажем равенство (3.1). Рассмотрим функцию f (x)

sin x

. Так как

sin( x)

sin x

sin x

x

f ( x)

f (x) ,

x

x

x

то функция

f (x) является четной, поэтому достаточно рассмот-

реть ее при

x 0 . Так как x 0 , то достаточно взять

x

. По-

2

строим круг радиуса R с центром в точке O (рис.10),

угол BOA ,

равный x радиан, треугольники OAB,

OAC и сектор

OAB . Оче-

видно, что

B

C

x

A

O

Рис.10

	S ОАВ Sсект.ОАВ S ОСА , или	1	R2 sin x	1	R2	x	1	R R tg x , или	sin x x tg x .
		2		2			2

Поделив на sin x ( sin x 0 , так как 0 x / 2) , получим:

11

1

x

1

или

cos x

sin x

1.

sin x

cos x

x

Так как lim cos x 1,

lim 1 1,

то по теореме о пределе промежуточной функции

x 0

x 0

имеем: lim

sin x

1 .

x 0 x

Следствие.

lim

tg x

1,

lim

arcsin x

1,

lim

arctg x

1.

x

x 0

x

x 0

x 0

x

Доказательство. 1). lim

tg x

lim

sin x

= lim

sin x

lim

1

1 1 1..

cos x x

cos x

x 0

x

x 0

x 0

x

x 0

2). Для отыскания

lim

arcsin x

сделаем замену

arcsin x y .

Тогда x sin y и

x 0

x

при x 0 .

Поэтому

y arcsin x 0

lim

arcsin x

lim

y

lim

1

1

1

1.

x

sin y

sin y

x 0

y 0 sin y

y 0

lim

1

y

y

y 0

3). Для отыскания

lim

arctg x

аналогично следует сделать замену arctg x y .

x

x 0

3.4. Сравнение бесконечно малых

Бесконечно малые функции часто сравнивают между собой по «быстроте»

стремления к нулю. Так, например, из двух функций

(x) x и (x) x10 бес-

конечно малых при

x 0

функция x10 стремится к нулю «быстрее», чем x .

Уточним, какой смысл вкладывается в слово «быстрее».

Пусть (x)

и (x) бесконечно малые функции при x a .

1). Если lim

(x)

конечен и отличен от нуля, то (x) и (x) называют беско-

x a (x)

нечно малыми одного порядка и обозначают так: ( x) O ( (x)) при x a .

В частности, если lim

(x)

1,

то

(x)

и (x) называют эквивалентными бес-

x a (x)

конечно малыми и обозначают так: (x) (x)

при x a .

2). Если lim

(x)

0,

то (x)

называют бесконечно малой более высокого

(x)

x a

порядка, чем x

и обозначают так: ( x) о ( ( x)) при x a .

3). Если lim

(x)

,

то

lim

(x)

0

и (x)

будет бесконечно малой более

x a (x)

x a (x)

высокого порядка, чем

(x) при x a .

4). Если lim

(x)

не существует, то (x)

и (x) называют несравнимыми

x a (x)

бесконечно малыми при x a .

Пример 3.4. Функции

x,

sin x,

tg x, arc sin x,

arctg x

являются эквивалентными

бесконечно малыми при x 0 , т.е.

12

sin x x ,

tg x x ,

arcsin x x ,

arctg x x

при x 0 .

Это вытекает из первого замечательного предела и его следствия.

Пример 3.5. Сравнить при x 0 бесконечно малые

(x) 1 cos 6x

и (x) x2 .

Решение.

1 cos 6x

2sin2 3x

sin 3x 2

lim

lim

18

lim

18.

x 0

x2

x 0

1

(3x)2

x 0 3x

9

Следовательно,

функции 1 cos 6x и

x2

являются бесконечно малыми одного

порядка при x 0 .

Для нахождения пределов важна следующая теорема.

Теорема 3.4 (об эквивалентных бесконечно малых).

Пусть ( x) ~ 1 ( x),

( x) ~ 1 ( x) при x a . Тогда

lim

(x)

lim

1(x)

.

x a (x)

x a (x)

1

Доказательство. Так как (x) ~ 1(x),

(x) ~ 1(x)

при x a , то lim

(x)

1,

x a (x)

(x)

(x)

(x)

1(x)

1(x)

1

lim

1.

Запишем равенство

и перейдем в нем к пределу:

(x)

1(x)

(x)

x a (x)

1(x)

1

1(x)

1 (x)

1(x)

(x)

(x)

lim

lim

lim

lim

lim

.

(x)

1

(x)

(x)

(x)

1(x)

x a

x a

x a 1

x a

x a

Пример 3.6.

Найти а)

lim

arctg 5x

,

б)

lim

tg (5x x3 ) (1 cos x)

.

x 0

sin 3x

x 0

arcsin3 (2x)

Решение. Имеем неопределенности вида

0

. Для их раскрытия заменим беско-

нечно малые функции на эквивалентные:

0

arctg 5x

0

5x

5

а) так как arctg 5x 5x ,

sin 3x 3x

при x 0 , то

lim

lim

;

sin 3x

3x

3

x 0

0

x 0

x

x 2

x2

б) так как tg (5x x3 ) ~ 5x x3,

1 cos x

2 sin2

~ 2

, arcsin3 2x ~ (2x)3 , то

2

2

2

tg 5x x3

1 cos x

0

x 5 x2

x2

5 x

2

5

lim

lim

2

lim

.

3

3

x 0

arcsin

2x

x 0

8x

x 0

16

16

0

Примеры для самостоятельного решения

Вычислить пределы: 1)

lim(x ctg 3x) ,

2)

lim

sin 5x sin 3x

, 3) lim

1 cos x2

,

1 cos x

x 0

x 0

sin x

x 0

4) lim (1 x) tg

x

( сделать замену переменной 1 x t ).

2

x 1

,

Ответы: 1)

1 ,

2) 2 ,

3)

2

4)

2

.

3

13

4. Бесконечно большие функции

4.1. Определение и основные свойства

Функция f x называется бесконечно большой при x a , если		lim f (x) .
		x a
Различают	частные случаи бесконечно больших функций, когда
lim f x или	lim f x .
x a	x a

Рассмотрим некоторые свойства бесконечно больших функций.

Теорема 4.1 (о связи с бесконечно малой).

Функция

f (x) бесконечно

большая

при x a тогда и

только

тогда, когда

функция

1

бесконечно малая при x a .

f ( x)

Доказательство. Функция f (x) бесконечно большая при x a , значит

lim

f (x) .

Тогда из определения предела следует, что для

0 , а значит и

x a

1

1

1

1

для

0 :

f (x)

для

x S (a) . Поэтому

=

для

f x

1

1

f x

. Это и означает, что lim

1

0 , то есть функция

1

является бес-

x S (a)

f (x)

x a

f (x)

конечно малой при x a . Аналогично доказывается и обратное утверждение.

Теорема 4.2 (об арифметических операциях).

1). Произведение двух бесконечно больших при x a есть бесконечно большая при x a .

2). Произведение бесконечно большой при x a на функцию, имеющую нену-

левой предел при x a , есть бесконечно большая при x a .

3) . Отношение бесконечно большой при x a к бесконечно малой (отличной от нуля) при x a есть бесконечно большая при x a .

4). Сумма двух бесконечно больших одного знака при x a есть бесконечно большая того же знака при x a .

Доказательство проведем для утверждений 1) и 3).

1). Пусть f (x) и g(x) бесконечно большие при x a . Тогда		1			,		1		есть
			f (x)					g(x)
бесконечно малые при x a . Значит и их произведение	1			1			является бес-
	f (x) g(x)
конечно малой при x a . Поэтому из теоремы 4.1 следует, что						f (x) g(x) явля-
ется бесконечно большой при x a .

3). Пусть функция f (x) бесконечно большая при x a , ( x) бесконечно малая

	при x a . Тогда			1	бесконечно большая и произведение двух бесконечно
			( x)
	больших f (x)	1		есть бесконечно большая при x a .
	(x)

14

Пример 4.1. Вычислить пределы: a)

lim

x

, б)

lim (a xn a

xn 1 a ),

(a

0) .

Решение.

x 1 x 1

x

0

1

n

0

а).

При

x 1 функция

x 1

является бесконечно малой, а функция

1

бесконечно большой. Произведение бесконечно большой функции

1

на

x 1

x 1

функцию x ,

имеющую ненулевой предел при

x 1 , есть бесконечно большая

функция. Значит,

lim

x

.

x 1 x 1

б). Функция P (x) a xn

a

xn 1 a

xn a

a1

an

при x

есть произ-

n

n

0

1

0

x

xn

a1

an

ведение

бесконечно

большой

xn

и

функции

a

,

имеющей

0

x

xn

при x ненулевой предел a0 . Поэтому функция Pn(x)

есть бесконечно большая

при x .

4.2. Неопределенности

,

0 ,

Рассмотрим функции

f (x) x ,

f

2

(x) x2 ,

f

(x) 3x ,

f

4

(x) x 1 . Эти функции

1

3

1

являются

бесконечно

большими

при

x ,

а

функции

1(x)

,

f1(x)

1

2 (x)

являются бесконечно малыми при

x .

f2 (x)

f3 (x)

f1(x)

1

f2 (x)

1). Так как lim

lim

0,

lim

lim x ,

lim

k , то предел

f (x)

x

f

2

(x)

x x

x

x

x

f (x)

1

1

отношения двух бесконечно больших функций может быть любым; его называ-

ют неопределенностью вида
						.
2). Так как lim
	f	(x) (x) lim x ,
x	2	1	x

lim f3 (x) 1(x) k, то предел произведения

x

бесконечно большой функции на бесконечно малую может быть любым; его называют неопределенностью вида 0 .

3). Так как lim [ f3	(x) f1	(x)] lim k 1 x k 1 ,	lim [ f4 (x) f1(x)] 1, то предел
x		x	x

разности двух бесконечно больших функций может быть любым; его называют неопределенностью вида .

Рассмотрим некоторые способы раскрытия неопределенностей.

Пример 4.2. Найти предел отношения двух многочленов при x .

Решение. В примере 4.1 было установлено, что многочлены являются бесконечно большими функциями при x , значит предел их отношения есть неопре-

деленность вида					. Для раскрытия неопределенности сделаем преобразования:
									xn a0 a1 / x an / xn
	P (x)		a xn a xn 1			a	n			a0	0
	n		0		1						.
	Qk (x)								xk b0 b1 / x bk / xk
			b0 xk b1xk 1 bk							b0	0

15

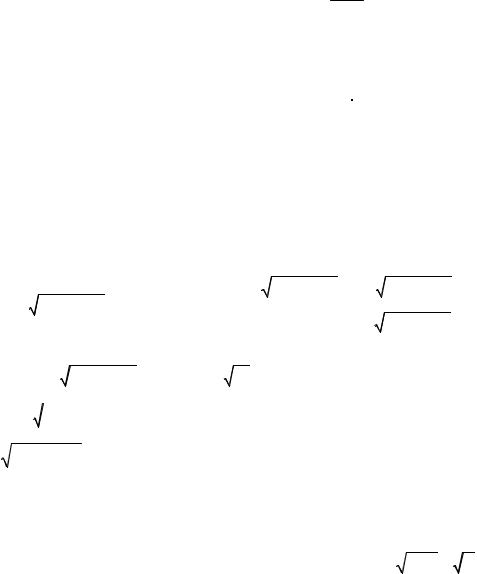
	a a		1	/ x a	n	/ xn		a
Функция	0						имеет ненулевой предел
								0
	b	b		/ x b		/ xk		b0
	0	1		k

	. Функция	xn	есть бес-
		xk

конечно большая при n k , бесконечно малая при n k и равна единице при n k .

		a xn a xn 1		a		,	n k,
Поэтому
	lim	0	1	n		0,	n k,
				b
	x b xk b xk 1				a / b , n k,
	0		1	k
						0	0

lim a0 xn

x b0 xk

,				n k,
		0,		n k,
a			/ b , n k.
	0			0

Следовательно,		a xn a xn 1		a			a xn		(4.1)
	lim	0	1	n		lim	0	.
	x b xk b xk 1			b		x b xk
	0		1	k		0

Аналогично, при отыскании предела отношения иррациональных функций младшие степени можно отбросить (пример 4.5).

Пример 4.3.

Пример 4.4.

Пример 4.5.

Пример 4.6.

2x100 x63 75

2x100

2

lim

lim

lim

0.

120

5x

70

100

120

20

x

7x

x 7x

x 7x

(2n 1)4 (n 3)4

(2n)4 n4

15n4

15

lim

lim

lim

.

(2n 1)

4

(n 5)

4

4

n

4

17n

4

n

n (2n)

n

17

x

x

x2 2x 1

x2 2x 1

lim

x2

2x 1 x

lim

x

2

x

x

2x 1 x

lim

(x2

2x 1) x2

lim

2x

lim

2x

1.

x

x2 2x 1 x

x

x2 x

x

x x

x

.

x2

2x 1 x

lim

Здесь функции

x2 2x 1

и ( x)

есть бесконечно большие одного знака и их

сумма является бесконечно большой.

Примеры для самостоятельного решения

x4 x 5

(2x 3)3 x 5 5

Найти пределы 1)

lim

,

2) lim

, 3) lim

n 1

n .

3

7x 9

x

8

3x

4

9

x 10 x

x

n

Ответы. 1) ,

2) 8,

3)

0.

4.3.Второй замечательный предел. Неопределенность 1

Вматематике большую роль играют следующие пределы:

lim	1 1/ x x e,	lim	1 y 1/ y	e.	(4.2)
x		y 0

Здесь e иррациональное число, e 2, 7182 . Более точное вычисление числа e будет приведено далее, при рассмотрении формулы Тейлора.

Равенства (4.2) называют вторым замечательным пределом. Второе из этих равенств получается из первого при замене 1/ x на y . Вывод равенств (4.2) мы опустим.

16

ln x loge x

В математике и её приложениях большую роль играют показательная функция ex с основанием e и логарифмическая функция с основанием e.

Пример 4.7. Найти пределы а)				lim 1 x 1/ x ,		б) lim 1 2x 1/ x .
				x 0		x 0
Решение. а). Пусть y x . Тогда lim 1 x 1/ x lim 1 y 1/ y lim								1 y 1/ y 1		e 1 ,
				x 0		y 0	y 0
б)	lim 1 2x 1/ x	lim	1 2x 1/ 2 x 2		e2 .
	x 0	x 0
Замечания.	1). У функций f x 1 x 1/ x ,					g x 1 2x 1/ x	основания стремятся

к единице при x 0 , а показатели степени – к бесконечности. Но пределы этих

функций различны, поэтому их называют неопределенностью вида
				1 .
2). Для раскрытия неопределенности вида			удобно применять второй заме-
	1

чательный предел.

Пример 4.8. Найти lim				2 x	2		1		x2
								.
					2
x				2 x			5
Решение. Tак как lim		2x2 1				lim 2x2				1 ,
x 2x2 5							x 2x2

Преобразуем дробь, выделив единицу:

то имеем неопределенность вида
						1		.
	2x2 1	2x2 5 4	1		4		.
	2x2 5
		2x2 5			2x2 5
4x2

			2x2		1	x	2				4				2x2 5		2x2 5
Тогда	lim							lim		1					4			e 2 .
				2								2
			2x		5						2x		5
	x							x

Здесь мы воспользовались вторым замечательным пределом lim 1 y 1/ y e ,

y 0

где y

4

, и тем, что

lim

4x2

lim

4x2

2.

2x2 5

ln 1 x

x 2x2 5

x 2x2

0

1

1/ x

Пример 4.9.

lim

lim

ln

1 x lim

ln 1 x

ln e 1 .

x

x 0

0

x 0 x

x 0

Примеры для самостоятельного решения

Вычислить пределы:

1)

lim

x 3 x

,

2) lim 1 x

2

7 ctg2 x

,

x x 2

x 0

3)lim 1 tg x 1/ sin x (использовать теорему о пределе частного).

x 0 1 2sin x

Ответы: 1) e5 ; 2) e7 ; 3) 1 / e .

17

5.Непрерывные функции

5.1.Функции, непрерывные в точке

Функция f x	называется непрерывной в точке x0	, если lim	f ( x) f ( x0 ) .
		x x	0

Рассмотрим свойства функций, непрерывных в точке.

Теорема 5.1 (о приращении непрерывной функции).

Функция f x непрерывна в точке x0 тогда и только тогда, когда бесконечно

малому приращению аргумента соответствует бесконечно малое приращение функции в точке x0 .

Доказательство. Равенство		lim f (x) f (x0 ) , определяющее непрерывную в точ-
		x x 0
ке x0 функцию, эквивалентно равенству			lim f (x) f (x0) 0 . Разность x x0 есть
приращение аргумента	x,	а разность	x x0 0	есть приращение функции
			f (x) f (x0 )
f (x0 ) . Следовательно,	равенство lim f (x) f (x0)			эквивалентно равенству
		x x0

lim f (x0) 0 , которое означает, что бесконечно малому приращению аргумента

x 0

x соответствует бесконечно малое приращение функции f (x0 ) .

Теорема 5.2 (о непрерывности суммы, произведения, частного).

Сумма, разность, произведение конечного числа непрерывных в точке функций есть функция, непрерывная в этой точке. Частное непрерывных в точке функций есть функция непрерывная в этой точке, если знаменатель в этой точке отличен от нуля.

Доказательство проведем,	например,	для произведения двух функций f x и
g x , непрерывных в точке	x0 . Воспользуемся теоремой о пределе произведе-
ния, учитывая, что lim f (x) f (x0) , lim		g(x) g(x0) . Получим:
x x0	x x0
lim f x g x lim f (x) lim g(x) f (x0 ) g(x0 ) .
x x0	x x0	x x0

Это равенство означает, что функция f x g x непрерывна в точке x0 .

Теорема 5.3 (о непрерывности элементарной функции).

Если элементарная функция определена в точке x0 и её окрестности, то она непрерывна в этой точке.

Доказательство. Из теоремы о пределе элементарной функции			f x следует,
что	lim	f (x) f (x0 ) , что и означает непрерывность функции f x в точке x0 .
	x x0	5.2. Точки разрыва функции и их классификация
	Из	определения функции f x , непрерывной в точке x0 ,	следует, что
lim	f (x) f (x0) . Это равенство означает выполнение трех условий:
x x0

18

1)	функция f x	определена в точке x0 и ее окрестности,
2)	функция f x	имеет предел при	x x0 или, что равносильно, равны одно-
	сторонние пределы f (x0 0) и f (x0		0) ,
3)	предел функции f x при x x0 равен значению функции в точке x0 .
	Если нарушается хотя бы одно из этих условий, то точку x0 называют точ-
кой разрыва функции. Выделяют следующие типы точек разрыва.
	1. Если в точке разрыва x0 существуют односторонние конечные пределы
функции, то x0 называют точкой разрыва первого рода.				При этом,
	а) если односторонние пределы совпадают, то x0			называют
	точкой устранимого разрыва первого рода,
	б) если односторонние пределы не совпадают, то x0 называют
	точкой конечного разрыва первого рода (или точкой скачка).

2. Если в точке x0 хотя бы один из односторонних пределов функции не су-

ществует или бесконечен, то x0 называют точкой разрыва второго рода.

	На рис.11 изображены различные типы точек
	разрыва.		y
	Точка x1 – точка разрыва, так как f x не опре-
	делена в точке x1 ; разрыв − устранимый, так как
	односторонние пределы совпадают. Для «устра-
	нения» разрыва в точке x1 нужно доопределить
				x1 x2 x3	x4
	функцию, положив f (x1 ) lim f (x) .
			x x1
	В точке x2		– устранимый разрыв первого рода,	Рис.11
	так как односторонние пределы совпадают, но
	f (x2 )	lim	f x . Для «устранения» разрыва в точке x2	нужно изменить значе-
		x x2
	ние функции в точке x2 , положив f (x2 ) lim f (x) .
			x x2
	В точке x3		– конечный разрыв первого рода (скачок),	так как односторонние
	пределы f (x3 0) , f (x3 0) конечны, но различны.
	В точке x4 – разрыв второго рода, так как правосторонний предел f x4				0 .

Пример 5.1. Установить тип точки разрыва функции f x 21/ x . Построить при-

мерный график функции.										y
Решение. Функция f x 21/ x не определена при x 0 , зна-
чит x 0 является точкой разрыва функции. Найдем пределы:										1
f 0	lim	2 1/ x 0 ,	так как	1				при	x 0 ,
	x 0			x
f 0	lim	21/ x ,	так как		1			при	x 0 .	Рис.12
	x 0				x

x

x

19

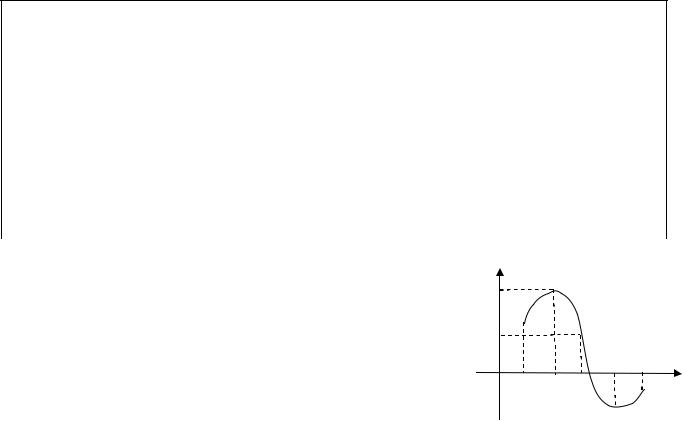
Так как f 0 , то x 0 является точкой разрыва второго рода.		Для построе-
ния графика функции (рис.12) воспользуемся тем, что	lim 21/ x 20	1.
	x			,
			2		x 0,
Пример 5.2. Исследовать на непрерывность функцию	ln 5 x
	f (x)
	sin(7x3 ), x 0.

Решение. Функции ln 5 x2 и sin (7x3 ) определены для любых x , являются

элементарными, а значит и непрерывными. Разрыв функции может быть только в точке «стыка» x 0 . Найдем односторонние пределы функции в этой точке:

lim	f (x) lim	ln(5 x2 )		ln 5,	lim	f (x)	lim sin 7x3 sin 0.
x 0	x 0				x 0		x 0

Так как односторонние пределы конечны, но различны, то x 0 есть точка конечного разрыва первого рода. Скачок функции в этой точке равен ln 5 .

5.3. Функции, непрерывные на отрезке

Функция f x называется непрерывной на отрезке				a, b , если
f x непрерывна в любой точке x0 a, b , т.е. lim f (x) f (x0 ),
f x	непрерывна в точке а справа,	т.е.	x x0
			lim	f (x) f (a),
f x	непрерывна в точке b слева,	т.е.	x a 0
			lim	f (x) f (b).
			x b 0

Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теоремы, не приводя доказательство.

Теорема 5.4. Пусть функция f x непрерывна на отрезке a, b . Тогда:

1) функция	f x	ограничена на отрезке a, b ,
2) функция	f x	достигает на отрезке a, b своего наибольшего и

наименьшего значения,

3) функция f x принимает на отрезке a, b все промежуточные значения

между наибольшим и наименьшим,

4) если на концах отрезка функция f x принимает значения разных знаков, то

	на интервале a, b найдется хотя бы одна точка с, в которой функция		f x
	принимает нулевое значение.
	Эта теорема имеет наглядную иллюстрацию. На	y
	рис.13 приведен график непрерывной функции f x .
		M
	Очевидно, что f x ограничена на отрезке a, b ; дости-
	гает наибольшего значения M в точке x1 , наименьшего	K
	значения m в точке x2 ; для любого числа K m, M
		x	x2	b	x
	найдется точка с такая, что f (c) K . Так как значения	3
		a x1 c

m

20

Рис.13