
- •§ 1. Вычисление площадей плоских фигур
- •1. Внешние, внутренние и граничные точки плоских множеств.
- •§2. Вычисление объёмов тел.
- •2. Объём прямого цилиндрического тела.
- •3. Вычисление объёма тела по площадям параллельных сечений.
- •§3. Вычисление длин дуг.
- •2. Достаточное условие спрямляемости прямой.
- •§4. Площадь поверхности вращения.
§3. Вычисление длин дуг.
Понятие спрямляемой дуги.
В школьном курсе математики рассматривался вопрос о вычислении длин отрезков прямой, длины окружности, а также различных её частей. В приложениях математики возникает потребность в вычислении длин дуг произвольных кривых. Но, чтобы вычислить длину произвольной кривой, надо быть уверенным в том, что рассматриваемая кривая имеет конечную длину.
В средней школе длиной окружности называют предел последовательности периметров вписанных в окружность правильных многоугольников ( при неограниченном удвоении числа сторон). Однако это определение неприменимо к произвольным кривым.
Дадим общее определение понятия длины кривой. Пусть задана жорданова кривая Г1:
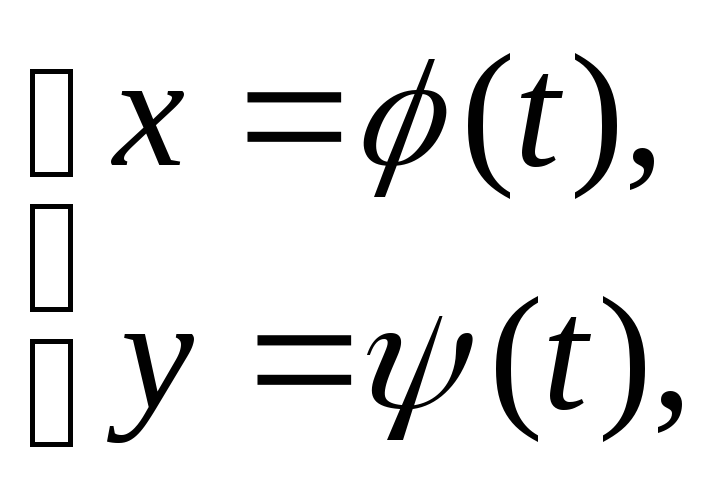 (1)
(1)
a ![]() t
t ![]() в.
в.
Напомним, что функции
![]() и
и![]() непрерывны
на отрезке. Разобьём отрезок [а;в]
на части числами
непрерывны
на отрезке. Разобьём отрезок [а;в]
на части числами
t0,t1,…,tn:a=t0<t1< … <tn=в.
Каждому числу tсоответствует
точка Мк(![]() ,
,![]() )
кривой Г. Проводя отрезки М0М1,
…,Mn-1Mn,
получим ломаную линию ɣ, вписанную в
кривую Г. Обозначим её длину черезl(ɣ).
)
кривой Г. Проводя отрезки М0М1,
…,Mn-1Mn,
получим ломаную линию ɣ, вписанную в
кривую Г. Обозначим её длину черезl(ɣ).
Определение.Жорданова кривая
(1) называется спрямляемой (имеющей
длину), если множество![]() длин вписанных в эту кривую ломаных γ
ограничено сверху. Точная верхняя
граница множества
длин вписанных в эту кривую ломаных γ
ограничено сверху. Точная верхняя
граница множества![]() называется длиной кривой Γ и обозначается
называется длиной кривой Γ и обозначается![]() :
:
![]() .
(2)
.
(2)
Докажем, что длина спрямляемой кривой обладает свойством аддитивности.
Пусть жорданова кривая Γ разбита на
кривые ![]() и
и![]() .
Если эти кривые спрямляемы, то кривая
Γ спрямляема, причем
.
Если эти кривые спрямляемы, то кривая
Γ спрямляема, причем![]() .
.
В самом деле, пусть γ – любая ломаная,
вписанная в кривую Γ, и пусть М – точка,
разбивающая Γ на ![]() и
и![]() .
Добавляя эту точку к вершинам ломаной
γ, получим ломаную
.
Добавляя эту точку к вершинам ломаной
γ, получим ломаную![]() ,
длина которой не меньше длины ломаной
γ,
,
длина которой не меньше длины ломаной
γ,![]() .
Но ломаная
.
Но ломаная![]() состоит из двух частей
состоит из двух частей![]() и
и![]() ,
вписанных соответственно в кривые
,
вписанных соответственно в кривые![]() и
и![]() ,
причем
,
причем![]() и
и![]() .
.
Поэтому
![]() .
.
Это неравенство показывает, что число
![]() является одной из верхних границ для
множества
является одной из верхних границ для
множества![]() длин ломаных, вписанных в кривую Γ. Но
для любого
длин ломаных, вписанных в кривую Γ. Но
для любого![]() найдутся ломаные
найдутся ломаные![]() и
и![]() ,
вписанные в
,
вписанные в![]() и
и![]() ,
такие, что
,
такие, что
![]() и
и![]() .
.
Объединяя ![]() и
и![]() ,
получаем ломаную γ, вписанную в Γ и
такую, что
,
получаем ломаную γ, вписанную в Γ и
такую, что
![]() .
.
А это и значит, что ![]() - точная верхняя граница множества
- точная верхняя граница множества![]() ,
т.е.
,
т.е.
![]() .
.
2. Достаточное условие спрямляемости прямой.
Назовем жорданову кривую Γ:
![]()
![]() ,
,
регулярной, если функции φ и ψ имеют на
отрезке ![]() непрерывные производные. Справедлива
следующая теорема.
непрерывные производные. Справедлива
следующая теорема.
Теорема 1.Всякая регулярная жорданова кривая Γ спрямляема.
Доказательство.
Разобьем отрезок ![]() на части точками
на части точками![]() и впишем в кривую Γ ломаную, соответствующую
этому разбиению. Рассмотрим одно звено
и впишем в кривую Γ ломаную, соответствующую
этому разбиению. Рассмотрим одно звено![]() этой ломаной,
этой ломаной,![]() ,
,![]() (рис. 49). Длина этого звена равна
(рис. 49). Длина этого звена равна
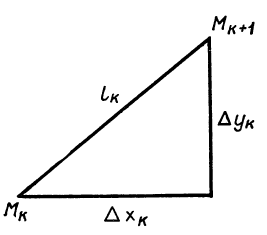
![]() .
.
Но по теореме Лагранжа найдутся такие
![]() и
и![]() ,
что
,
что
![]() ,
,
![]()
и поэтому
Рис. 49![]() .
.
Значит, длина всей ломаной выражается формулой
![]() .
(3)
.
(3)
По условию производные ![]() и
и![]() непрерывны на отрезке
непрерывны на отрезке![]() .
Поэтому для
.
Поэтому для![]() и
и![]() на отрезке
на отрезке![]() есть наибольшие значения. Обозначим их
А и В:
есть наибольшие значения. Обозначим их
А и В:
![]() ,
,![]() .
.
Но тогда
![]() ,
,![]() ,
,
а потому в силу (3)
![]() .
.
Поскольку ![]() , то для всех ломаных, вписанных в кривую
Γ,
, то для всех ломаных, вписанных в кривую
Γ,
![]() (4)
(4)
Поэтому кривая Γ спрямляема.
Отметим, что из равенства (3) вытекает также оценка длины ломаной снизу:
![]() ,
(5)
,
(5)
где α и β – наименьшие значения для ![]() и
и![]() на отрезке
на отрезке![]() .
.
Из неравенств (4) и (5) вытекают аналогичные неравенства для длины кривой:
(6)
![]() ,
,
(7)
![]() .
.
Неравенство (7) следует из неравенства
(5) и из того, что lкр![]() lлом.
Чтобы доказать неравенство (6), заметим,
что в силу неравенства (4)
lлом.
Чтобы доказать неравенство (6), заметим,
что в силу неравенства (4)![]() является одной из верхних границ для
длин вписанных в Г ломаных, числоlкр
– точная верхняя граница для этих
длин, т.е. наименьшая из верхних границ.
Отсюда и следует неравенство (6).
является одной из верхних границ для
длин вписанных в Г ломаных, числоlкр
– точная верхняя граница для этих
длин, т.е. наименьшая из верхних границ.
Отсюда и следует неравенство (6).
Вывод формулы длины дуги регулярной кривой.
Лемма.Пусть жорданова кривая регулярна иl (t)– длина дуги этой кривой, ограниченной точками М(а) и М(b). Тогда функцияl (t) дифференцируема на отрезке [a;b], причём для всехt имеем:
(8)
![]() .
.
Доказательство. Возьмём любое t
![]() [a;b]
и дадимtприращение
[a;b]
и дадимtприращение![]() такое, чтоt+
такое, чтоt+![]()
![]() [a;b].
Положим для определённости
[a;b].
Положим для определённости![]() >
0. Соответствующее приращение функцииl (t),
т.е.l (t
+
>
0. Соответствующее приращение функцииl (t),
т.е.l (t
+![]() ) - l (t),равно длине дуги кривой, ограниченной
точками М(t) и М(t+
) - l (t),равно длине дуги кривой, ограниченной
точками М(t) и М(t+![]() ).
В силу неравенств (6) и (7) п.2 имеем:
).
В силу неравенств (6) и (7) п.2 имеем:
![]()
![]()
![]()
![]() .
.
Перейдём к пределу при
![]()
![]() 0.
В силу непрерывности функций
0.
В силу непрерывности функций![]() и
и![]() в точкеtполучаем, что
в точкеtполучаем, что
![]()
и
![]() ,
,
а потому
![]() .
.
Лемма доказана.
Из этой леммы следует, что
(9)
![]()
Так как
![]() ,
,![]() ,
то формулу (9) можно переписать в виде
,
то формулу (9) можно переписать в виде
![]() .
.
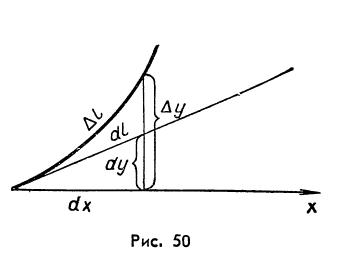
Геометрический смысл этой формулы ясен
из рисунка 50, где
![]() - участок дуги, а
- участок дуги, а![]() - соответствующий отрезок касательной.
Мы будем называть
- соответствующий отрезок касательной.
Мы будем называть![]() дифференциалом длины дуги кривой.
дифференциалом длины дуги кривой.
Теорема 2.Если жорданова кривая Г:
![]()
![]() ,
,
Регулярна, то его длина выражается формулой
(10) ![]()
Доказательство. Так как
![]() ,
то
,
то![]() - первообразная для
- первообразная для![]() ,
а тогда
,
а тогда![]() равна разности значений первообразной,
т.е.
равна разности значений первообразной,
т.е.
l=l(a)-l(b)=![]()
Теорема доказана.
Полученную формулу можно переписать в следующих видах:
(10')
![]()
(10'')
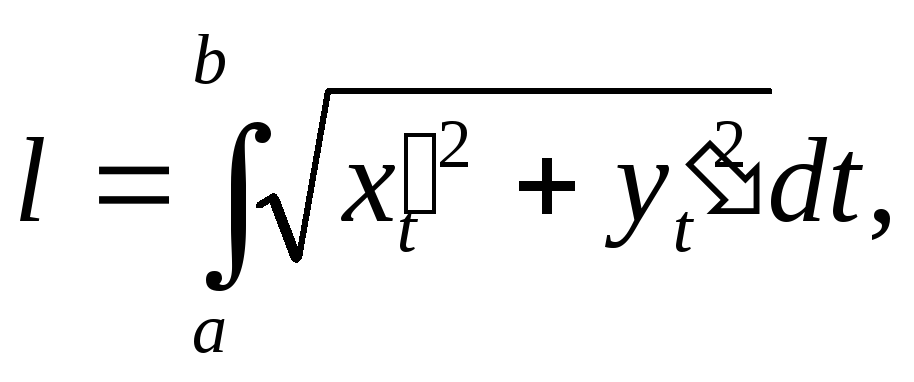
(10''')
![]()
Пример 1. Рассмотрим длину дуги астроиды
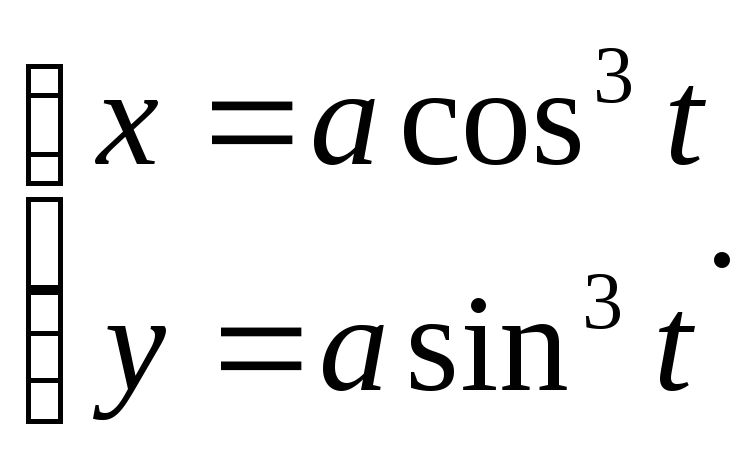 ,
,![]()
Решение. Данная кривая симметрична
относительно обеих координатных осей,
поэтому достаточно найти длину четверти
дуги, расположенной в первом квадранте
(![]() )
)
Найдём производные:
![]()
![]()
Вычислим сумму:
![]()
Учитывая сказанное выше, найдём четверть длины астроиды:
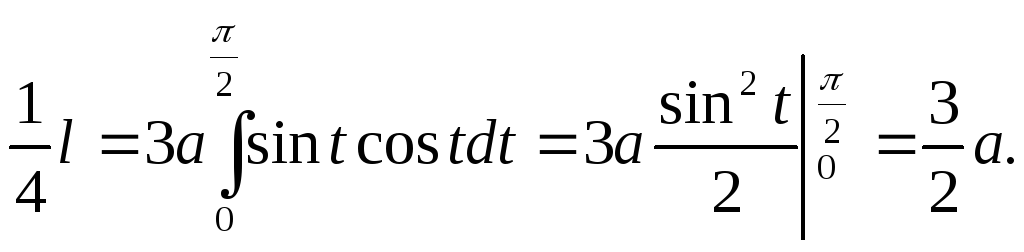
Длина всей кривой
![]() .
Она мало отличается от
.
Она мало отличается от![]() ,
т.е. от длины окружности, описанной
вокруг астроиды.
,
т.е. от длины окружности, описанной
вокруг астроиды.
4. Частные случаи формулы длины
кривой.Рассмотрим частные случаи
общей формулы (10) п.3. Если кривая Г задана
явным уравнением![]()
![]() то
её можно представить параметрическими
уравнениями
то
её можно представить параметрическими
уравнениями
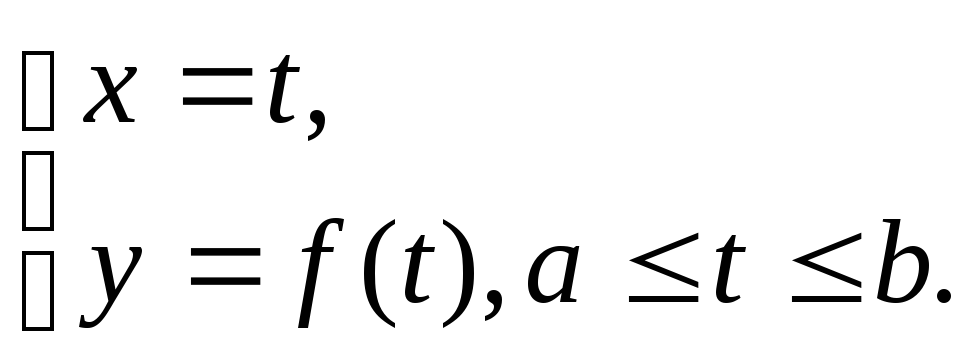 В
этом случае
В
этом случае
(11)
![]() .
.
Полученную формулу записывают короче в виде
(11')
![]()
Значит,
(12)
![]()
Пример 2. Вычислим длину дуги цепной
линии
![]() взятой от точки х=0 до точки х=1 (рис.51).
взятой от точки х=0 до точки х=1 (рис.51).
Найдём производную
![]()
Вычислим подкоренное выражение
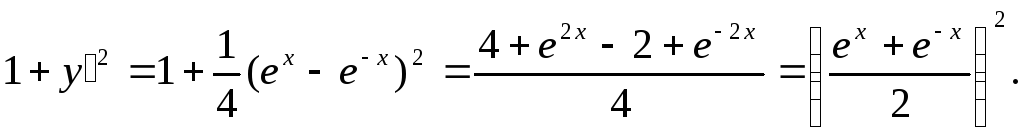
Длина l указанного отрезка цепной линии будет
![]()
Рассмотрим теперь случай, когда кривая
Г задана в полярных координатах уравнением
![]() ,
где
,
где![]() причём функция
причём функция![]() на отрезке [
на отрезке [![]() ]
имеет непрерывную производную
]
имеет непрерывную производную![]() .
.
Так как декартовы координаты связаны
с полярными координатами точек плоскости
соотношениями
![]()
![]() ,
полярное уравнение данной кривой можно
записать в виде параметрических
уравнений:
,
полярное уравнение данной кривой можно
записать в виде параметрических
уравнений:
![]() ,
,![]() ;
;
отсюда находим:
![]() ,
,![]()
Поэтому

![]() .
.
В силу формулы (10) п.3 имеем:
(13)
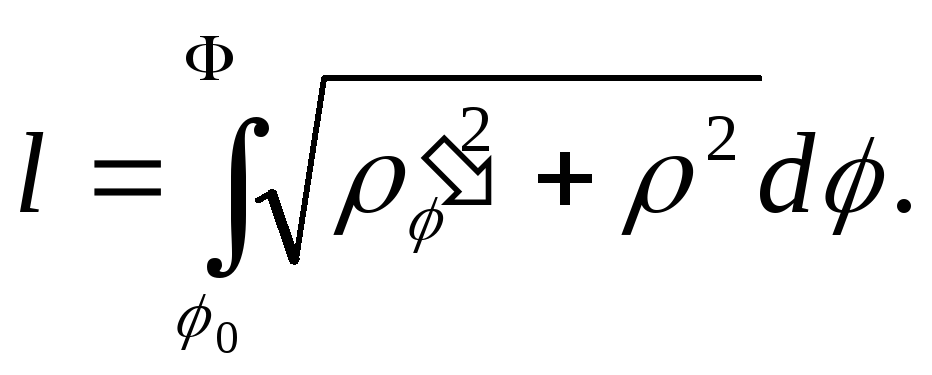
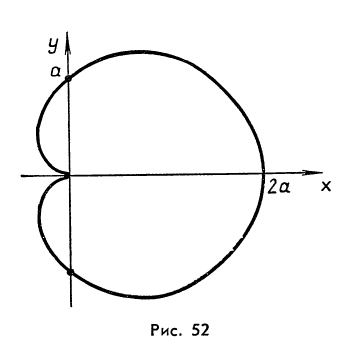
Пример 3. Вычислим длину кардиоиды
![]()
Решение. Данная функция
![]() чётная, следовательно, кривая расположена
симметрично относительно полярной оси
(рис.52).
чётная, следовательно, кривая расположена
симметрично относительно полярной оси
(рис.52).
Поэтому сначала найдём половину длины
дуги данной кривой, для которой полярный
угол
![]() изменяется от 0 до 2
изменяется от 0 до 2![]() ,
после чего удвоим полученный результат:
,
после чего удвоим полученный результат:
![]() .
.
Из формулы (13) получаем выражение дли дифферинциала дуги, заданной полярным уравнение
(14)
![]()
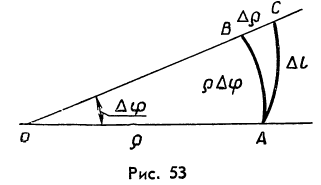
Геометрическую иллюстрацию даёт рисунок
53. На этом рисунке АС – дуга рассматриваемой
кривой, АВ – дуга окружности с центром
в точке О и радиусом
![]() ,
,![]() - длина дуги АВ. Заменяя
- длина дуги АВ. Заменяя![]() ,
,![]() и
и![]() соответственно
соответственно![]() ,
,![]() и
и![]() ;
рассматриваемый криволинейный треугольник
АВС как прямоугольный с катетами
;
рассматриваемый криволинейный треугольник
АВС как прямоугольный с катетами![]() и
и![]() и гипотенузой
и гипотенузой![]() .
Тогда
.
Тогда
![]()
5. Необходимое и достаточное условие спрямляемости кривой.Данное в п.2 условие спрямляемости кривой является достаточным, но не необходимым (например, любая ломаная спрямляема, но не регулярна, так как имеет точки излома).Чтобы сформулировать необходимое и достаточное условие спрямляемости кривой, нам понадобится понятие: функция с ограниченным изменением.
Рассмотрим функцию y=f(x), определённую на отрезке [a;b], и произвольное разбиение Р этого отрезка:
![]()
Для каждого частичного промежутка
![]() разбиения Р образуем разность
разбиения Р образуем разность![]() - приращение функции на этом промежутке.
Эта разность может быть как положительной,
так и отрицательной. Заменим все эти
разности их модулями и сложим. Получим
сумму
- приращение функции на этом промежутке.
Эта разность может быть как положительной,
так и отрицательной. Заменим все эти
разности их модулями и сложим. Получим
сумму
![]()
Полученная сумма называется изменением
функции
![]() ,
соответствующим разбиению Р отрезка
,
соответствующим разбиению Р отрезка![]()
Рассмотрим множество
![]() изменений функции
изменений функции![]() ,
,![]() соответствующих всевозможным разбиениям
отрезка
соответствующих всевозможным разбиениям
отрезка![]() Если это множество ограничено сверху,
то говорят, что функция
Если это множество ограничено сверху,
то говорят, что функция![]() имеет ограниченное изменение на отрезке
имеет ограниченное изменение на отрезке![]() ,
а точную верхнюю границу этого множества
называют изменением функции
,
а точную верхнюю границу этого множества
называют изменением функции![]() на отрезке
на отрезке![]() и обозначают
и обозначают![]() .
Таким образом,
.
Таким образом,
![]() .
.
Теперь мы можем сформулировать и доказать необходимое и достаточное условие спрямляемости жордановой кривой.
Теорема 3. Для того чтобы жорданова кривая Г:
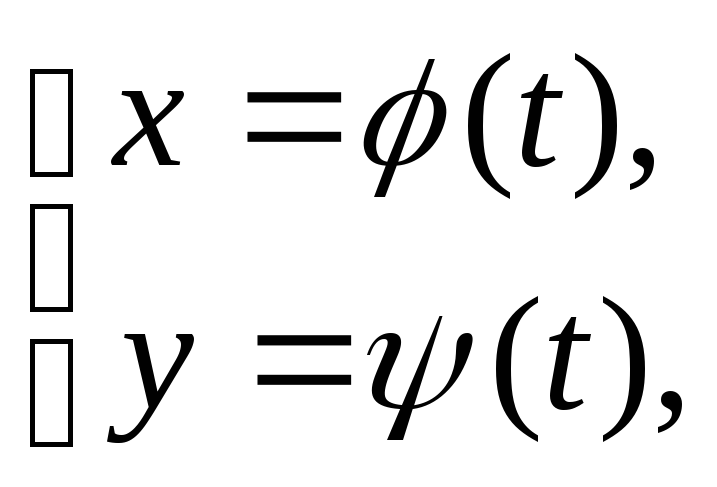 a
a ![]() t
t ![]() b.
b.
была спрямляемой, необходимо и достаточно,
чтобы непрерывные функции
![]() и
и![]() имели
ограниченное изменение на отрезке
имели
ограниченное изменение на отрезке![]() .
.
Доказательство. Покажем сначала, что
ограниченность изменения функции
![]() и
и![]() на
отрезке
на
отрезке![]() является необходимым условием
спрямляемости кривой Г. В самом деле,
если кривая Г спрямляема, то множество
является необходимым условием
спрямляемости кривой Г. В самом деле,
если кривая Г спрямляема, то множество![]() длин вписанных в неё ломанных ограничено
сверху некоторым числом М. Это означает,
что для любой вписанной в Г ломанной
имеем:
длин вписанных в неё ломанных ограничено
сверху некоторым числом М. Это означает,
что для любой вписанной в Г ломанной
имеем:
![]()
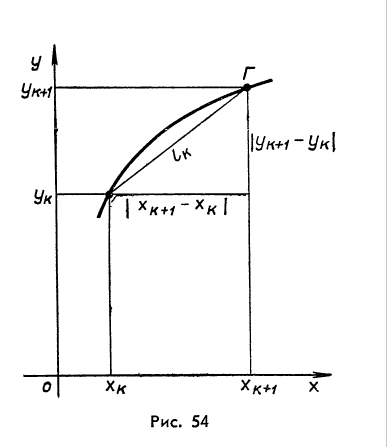
Но из рисунка 54 видно, что
![]() и
и![]() ,
а потому
,
а потому![]() и
и![]() .
.
Эти неравенства можно переписать следующим образом:
![]()
и
![]() .
.
Они показывают, что для любого разбиения
Р отрезка
![]() имеем
имеем![]() и
и![]() ,
т.е. функции
,
т.е. функции![]() и
и![]() имеют ограниченное изменение на отрезке
имеют ограниченное изменение на отрезке![]() .
.
Теперь докажем, что если функции
![]() и
и![]() имеют ограниченное изменение на отрезке
имеют ограниченное изменение на отрезке![]() ,
то кривая Г спрямляема на этом отрезке.
В самом деле, в этом случае существует
такое число М, что
,
то кривая Г спрямляема на этом отрезке.
В самом деле, в этом случае существует
такое число М, что
![]()
и
![]() .
.
Иными словами,
![]()
и
![]() .
.
Но из рисунка 54 видно, что
![]() .
.
Поэтому для любой ломаной
![]() ,
вписанной в кривую Г, имеем:
,
вписанной в кривую Г, имеем:
![]() ,
,
и потому кривая Г спрямляема.
