§ 3 Методы решения матричных игр

Я, конечно, живу в постоянной тревоге, играю по самой

маленькой и чего-то жду, рассчитываю, стою по целым

дням у игорного стола и наблюдаю игру. Ф. М.Достоевский «Игрок»

Наши рассмотрения мы начнем с матричных игр, число стратегий хотя бы одного из игроков в которых равно двум.

1.Для построения решений 2n и m2 игр существует эффективный метод, основанный напростых геометрических соображениях. Этот метод называют графическим. 2n игры. Пусть - платежная матрица2n игры.

Согласно теореме о двойном описании игры (теорема 2) нахождение цены игры и оптимального значения рдляигрока А равносильно разрешению уравнения

Опишем общую схему, приводящую к искомому результату. Максимум функции (*)проще всего найти, построив ее график. Для этого поступают следующим образом. Предположим, что игрок А выбрал смешанную стратегию Р = {р, 1 - р}, а игрок В — k-ю чистую стратегию, k: = 1, 2, …, n. Тогда средний выигрыш игрока А в ситуации {Р, k} оказывается равным Замечание. На плоскости уравнение (k) описывает прямую. Тем самым, каждой чистой стратегии игрока В на этой плоскости соответствует своя прямая.

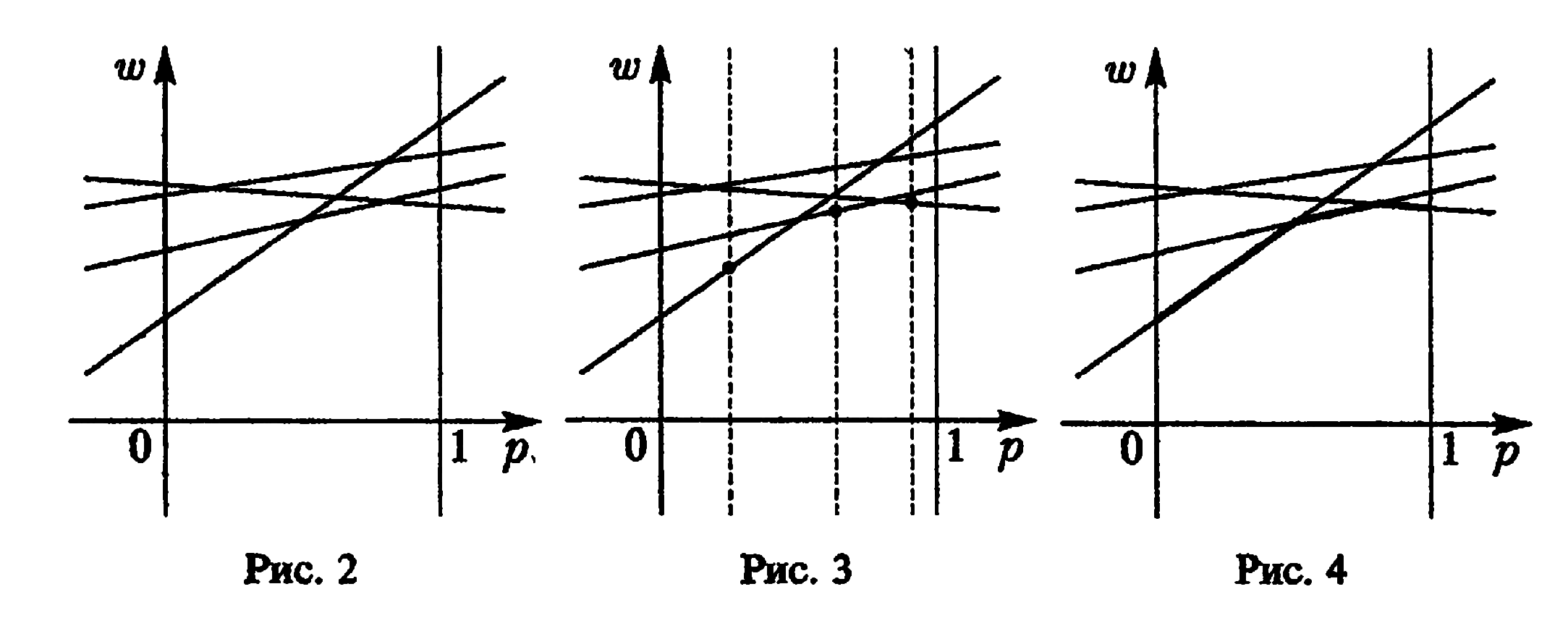
Поэтому сначала на плоскости последовательно и аккуратно рисуютсявсе прямые =1, 2, ...,n (рис.2). Затем для каждого значения р, 0 ≤ p ≤ 1, путем визуального сравнения соответствующих ему значений на каждой изпостроенных прямых определяется и отмечается минимальное из них (рис. 3). В результате описанной процедуры получается ломаная, которая и является графиком функции (*) (выделена жирным на рис. 4). Эта ломаная как бы огибает снизу все семейство построенных прямых, и по этой причине ее принято называть нижней огибающей этого семейства. Верхняя точка построенной нижней огибающей определяет и цену игры —v и оптимальную стратегию Р = {р,1 - р} игрока А (рис. 5). Замечание. Описанная процедура может рассматриваться как некоторый аналог максимального подхода при отсутствии седловой точки. Опробуем описанную схему решения 2n игры на конкретном примере. П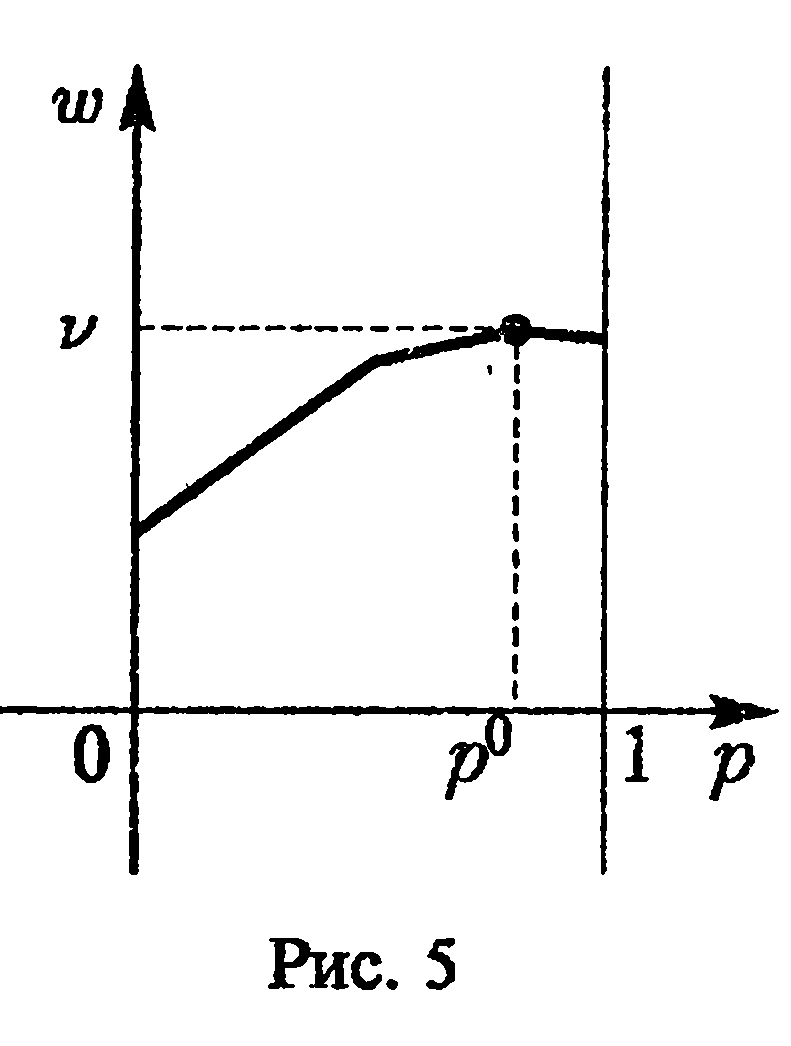ример5. Рассмотрим игру, заданную 26 матрицей

.

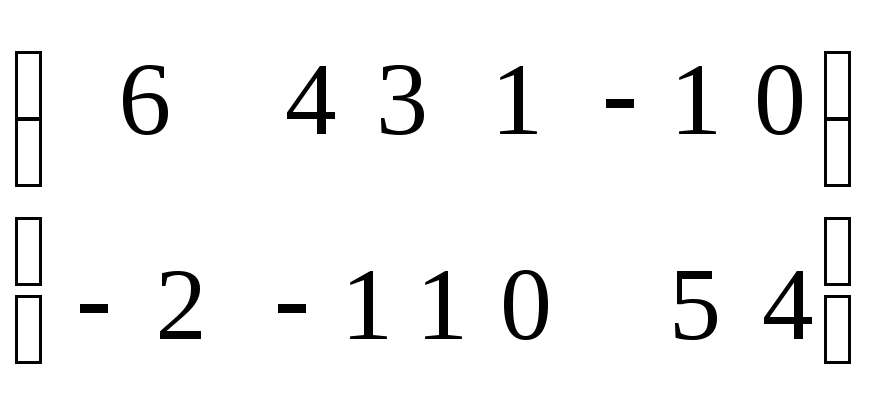Решение.

1) Анализ игры на наличие седловой точки. Нижняя цена игры равна -1, верхняя цена игры равна 1. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2) Вычисление средних выигрышей игрока А (проводится при условии, что игрок В выбирает только чистые стратегии). Из таблицы р 6 4 3 1 -1 0 1-р -2 -1 1 0 5 4

легко получаем: (1): (2): (3): (4): (5): (6):

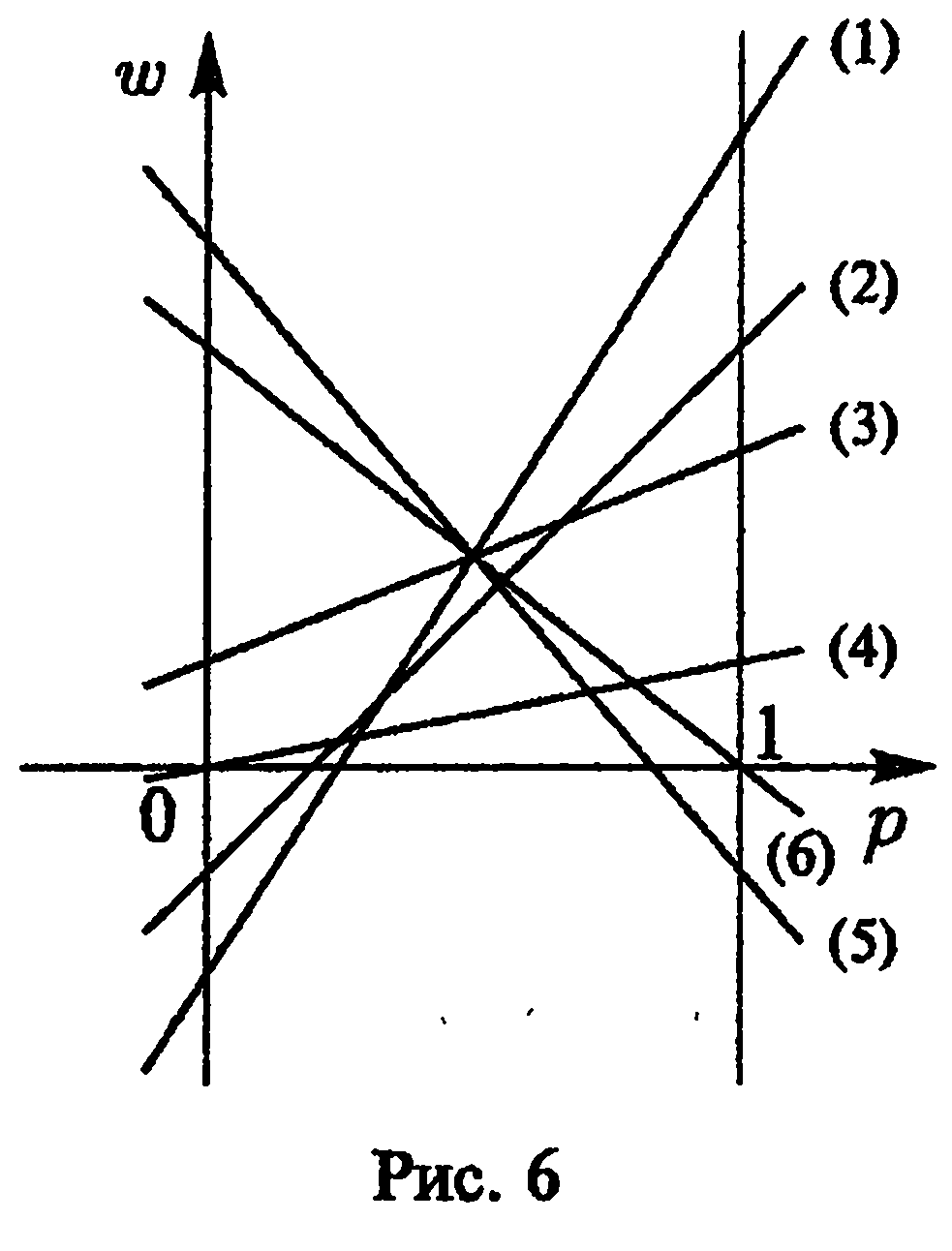
3) Построение нижней огибающей. Аккуратно строим на координатной плоскости все шесть прямых, уравнения которых получены на 2-м шаге (рис. 6), и находим их нижнюю огибающую.

4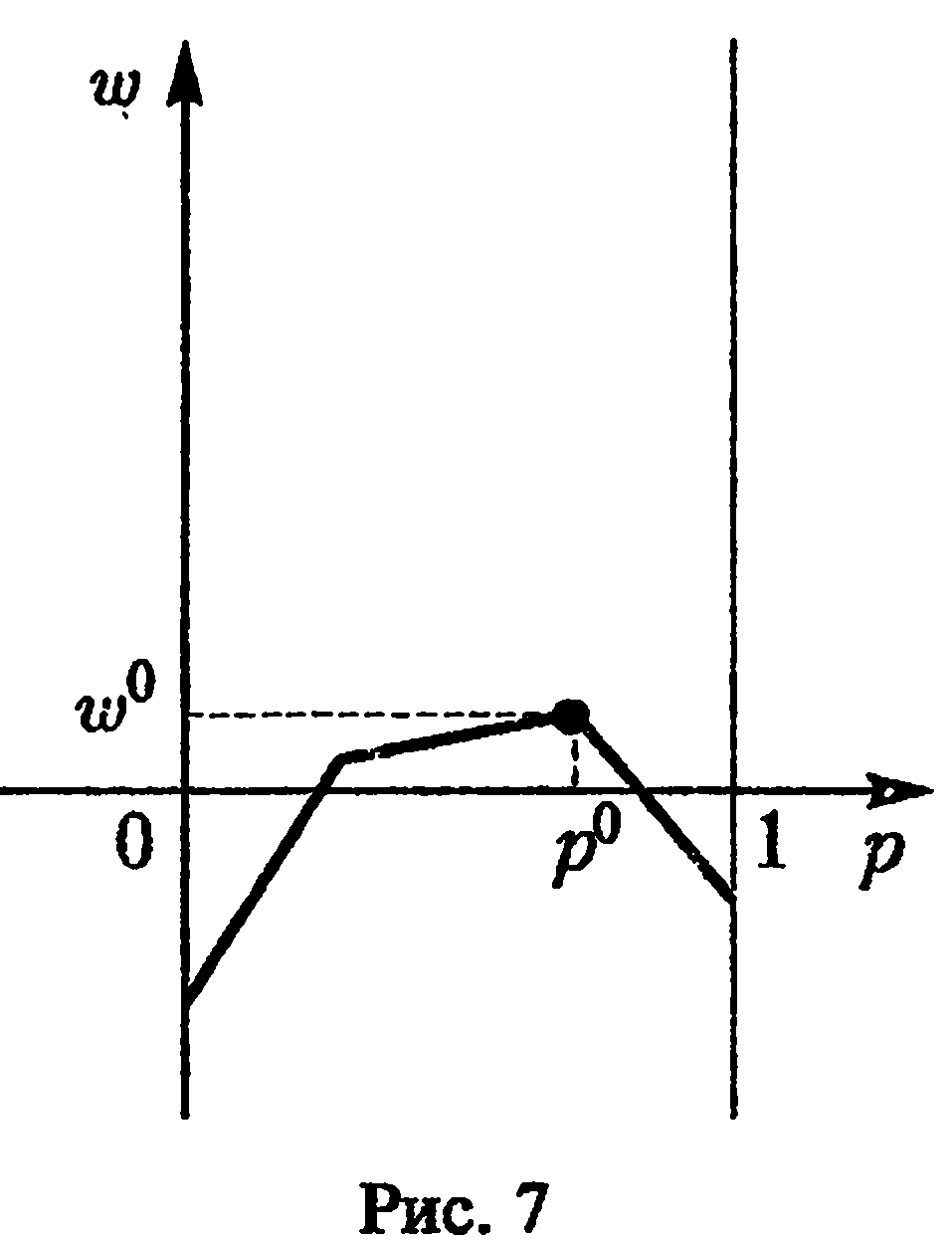)Отыскание цены игры и оптимальной смешанной стратегии игрока А.При аккуратном построении нижней огибающей нетрудно определить, какие две из построенных шести прямых пересекаются в ее наивысшей точке. В данном случае это прямые (4) и (5), заданные соответственно. Решая систему уравнений

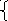
получаем (рис.7). Тем самым, цена игры v и оптимальная стратегия Ригрока А соответственно равны .

Этим заканчивается решение игры для игрока А, поскольку в первую очередь интересует отыскание собственной оптимальной стратегии и ожидаемого наилучшего гарантированного результата.

Замечание. Решающий матричную игру обычно отождествляет себя с одним из игроков (как правило, это игрок А), считая другого своим противником. Это связано еще и с тем, что в некоторых случаях основное внимание уделяется поиску оптимальных стратегий только игрока А, а стратегии противника могут вообще не интересовать исследователя.

Однако в целом ряде случаев оказывается важным знать оптимальные смешанные стратегии обоих игроков.

К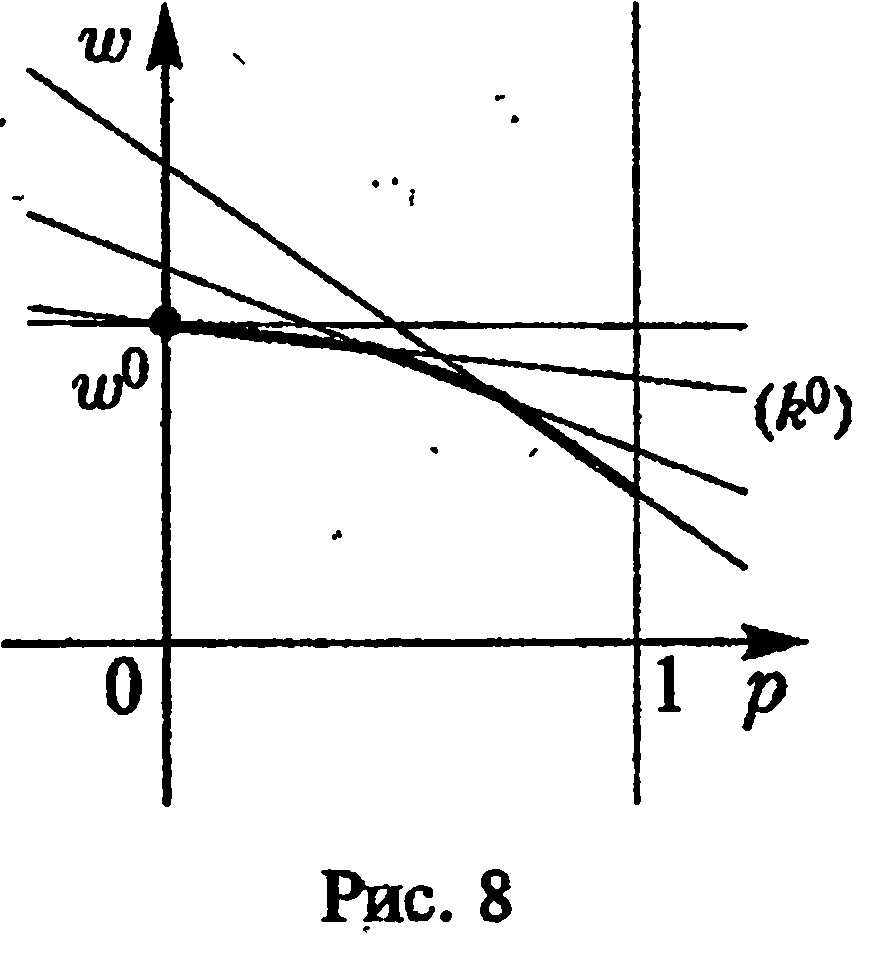ак ищется оптимальная смешанная стратегия игрокаА, мы уже описали. Покажем теперь, как отыскать оптимальную смешанную стратегию игрока В. Здесь, в зависимости от формы нижней огибающей, может представиться несколько случаев.

а) Нижняя огибающая имеет ровно одну наивысшую точку :

1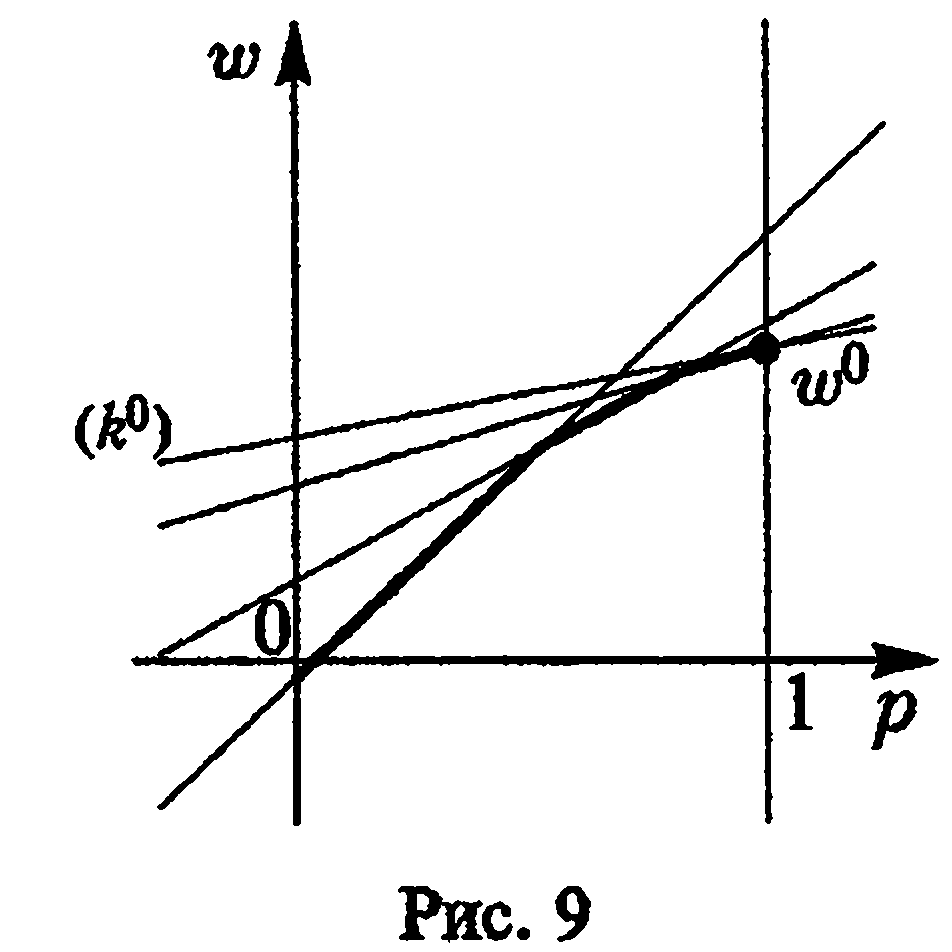. Если р= 0 (оптимальная стратегия игрока А -чистая стратегия А),то игроку В выгодно применять чистую стратегию, соответствующую номеру прямой, проходящей через точку (0,) и имеющей наибольшийотрицательный наклон (рис. 8).

2. Если р= 1 (оптимальная стратегия игрока А -чистая стратегия А),то оптимальной для игрока В является чистая стратегия, соответствующая номеру прямой, проходящей через точку (1, )и имеющей наименьший положительный наклон (рис. 9).

3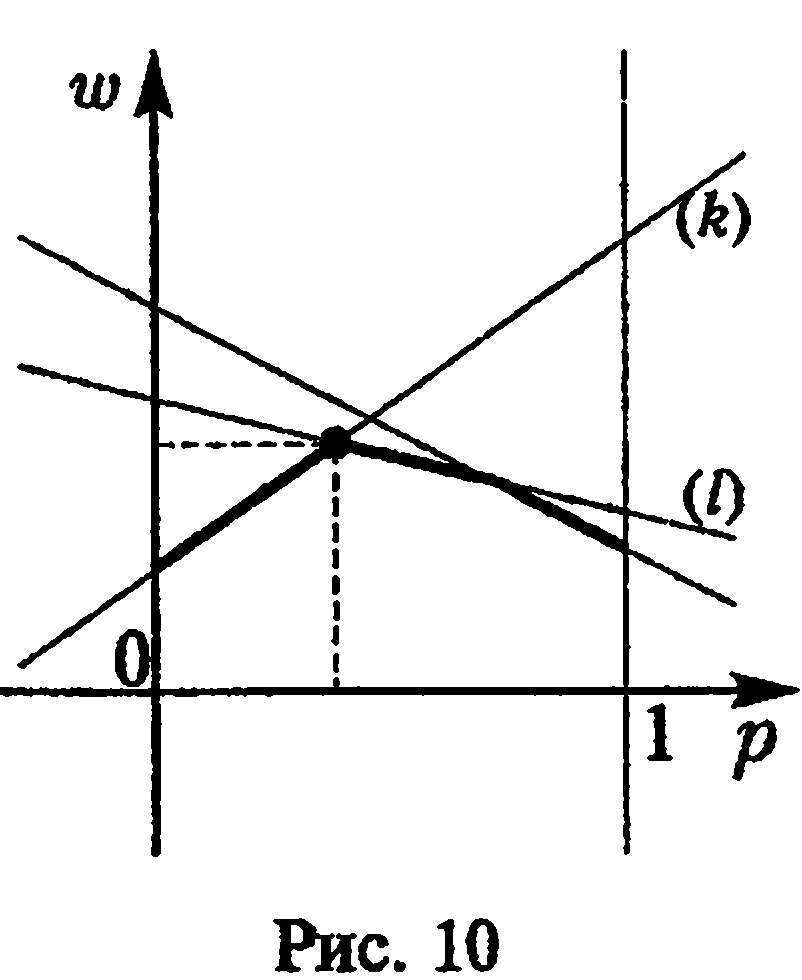. Если 0< р < 1, то в наивысшей точке нижней огибающей пересекаются, по меньшей мере, две прямые, одна из которых (k-я) имеет положительный наклон, а другая (l-я) — отрицательный (рис. 10), и оптимальная смешанная стратегия игрока В получается, если положить гдеq- решение уравнения .

б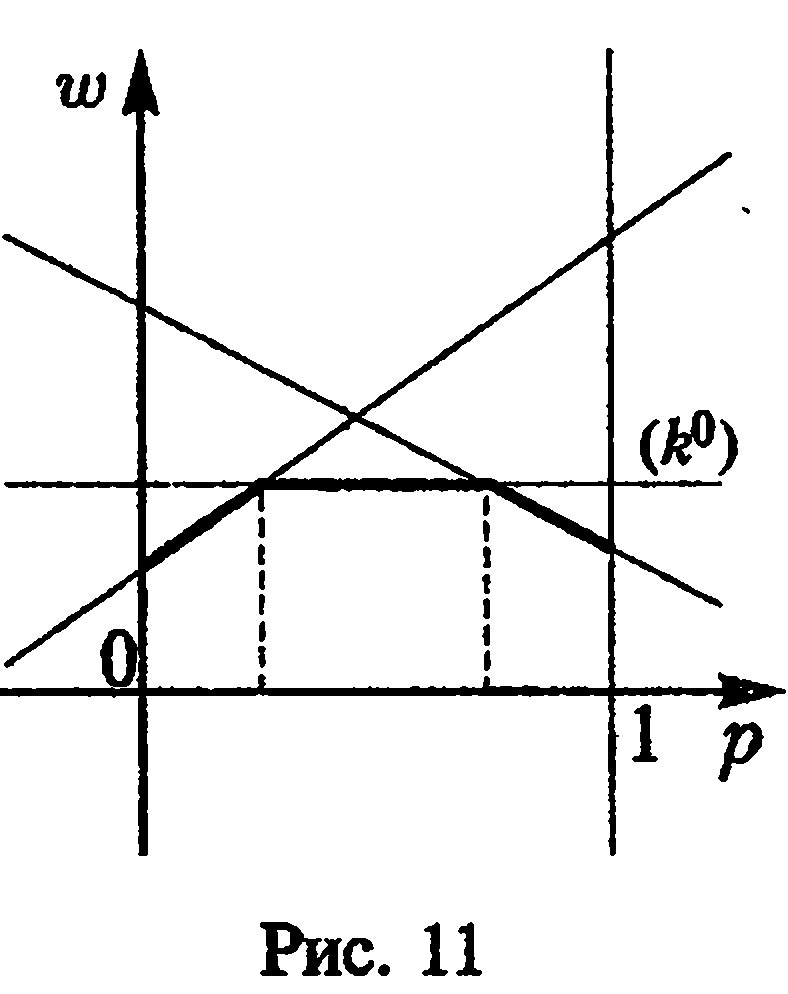) Нижняя огибающая содержит горизонтальный участок, соответствующий чистой стратегииигрокаВ, которая и является оптимальной для него (рис.11).

Пример 5 (продолжение). Покажем теперь, как найти полное решение игры, то есть еще и оптимальную смешанную стратегию игрокаВ.

1) Пусть , выделив тем самым изшести чистых стратегий игрока В стратегии Ви В,которым соответствуют прямые (4) и (5), определяющие наивысшую точку нижней огибающей.

2) Приравняем любой из двух средних выигрышей игрока В (игрок А выбирает только чистые стратегии), отвечающих предложенной смешанной стратегии

0 0 0 q 1-q 0

6 4 3 1 -1 0

-2 -1 1 0 5 4

к цене игры и

3) получают один и тот же результат .

Полное решение игры имеет следующий вид ,,.