
2M игры.
Пусть теперь в матричной игре две чистые стратегии имеет игрок В, а число чистых стратегий у игрока А произвольно (равно m). Это означает, что платежная матрица игры имеет вид:
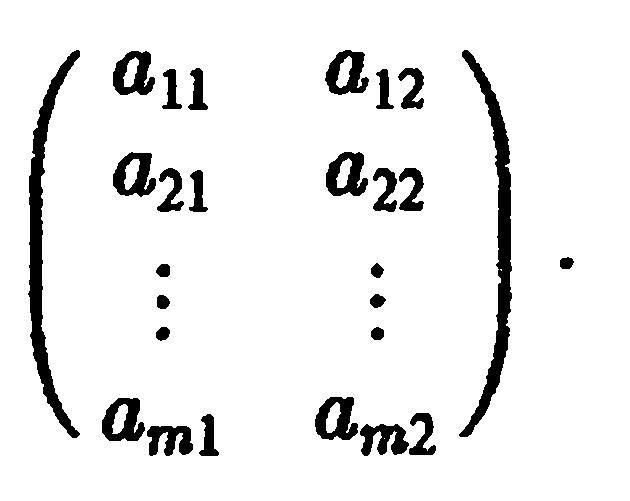
А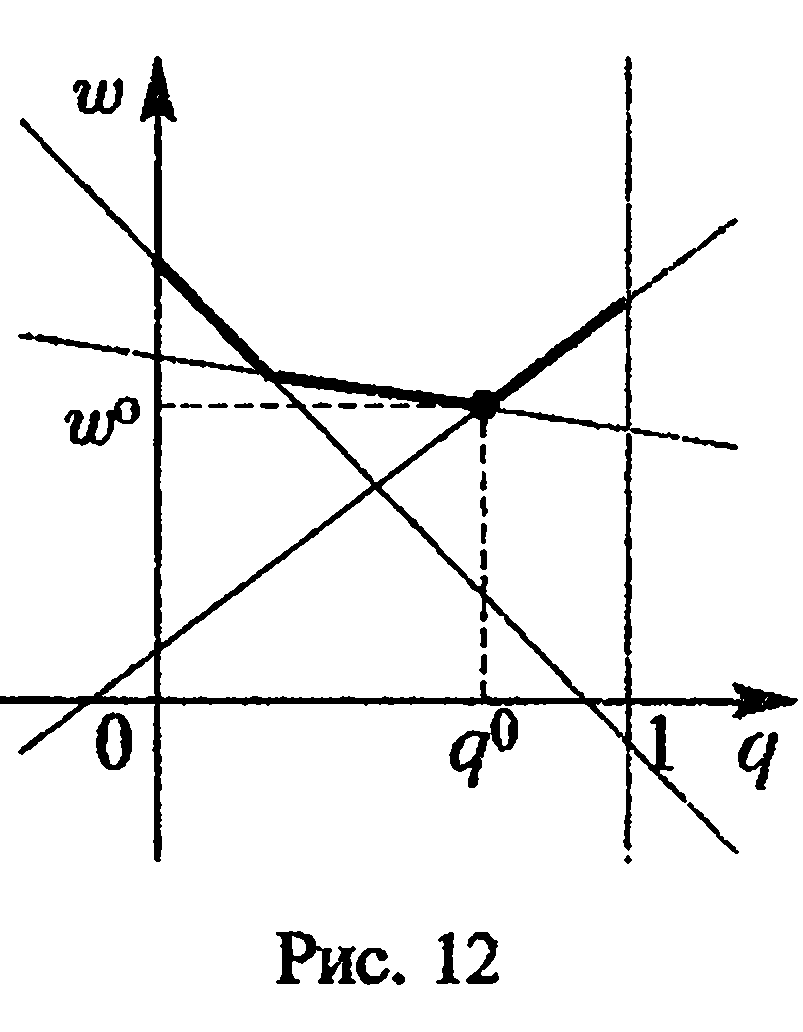 нализ
такой игрыво
многом напоминает
рассуждения, описанные для
игры 2
нализ
такой игрыво
многом напоминает
рассуждения, описанные для
игры 2![]() n.
n.
Пусть Q={q,
1-q}
- произвольная
смешанная стратегия игрока В.
Если игрок А
выбирает i-ю
чистую стратегию,
i =
1,2,...,m,
то средний выигрыш игрока
В в
ситуации {i,
Q}
будет равным![]() i=1,2,...,m.(*)
i=1,2,...,m.(*)
Зависимость этого
выигрыша от переменной q
описывается прямой. Графиком функции
![]() является верхняя огибающая семейства
прямых(*),
соответствующих
чистым стратегиям игрока А
(рис. 12).
является верхняя огибающая семейства
прямых(*),
соответствующих
чистым стратегиям игрока А
(рис. 12).
Абсцисса нижней
точки полученной ломаной определяет
оптимальную смешанную стратегию игрока
В, а
ордината
![]() -цену игры.
-цену игры.
Замечание.
Отыскание
оптимальной смешанной стратегии игрока
А проводится
по той же схеме, которая позволяет найти
оптимальную смешанную стратегию игрока
В в
игре 2![]() n.
Пример
6. 3 х 2 игра
задана матрицей
n.
Пример
6. 3 х 2 игра
задана матрицей
![]() .
.
Решение.
1) Анализ игры на наличие седловой точки. Нижняя цена игры равна 0, верхняя цена игры равна 3. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.
2 )
Вычисление средних выигрышей игрока В(игрок А
выбирает
только чистые стратегии). Из таблицы
q
1-q
3
-1
1
0
получаем: (1):
)
Вычисление средних выигрышей игрока В(игрок А
выбирает
только чистые стратегии). Из таблицы
q
1-q
3
-1
1
0
получаем: (1):
![]() (2):
(2):
![]() (3):
(3):
![]() .
.
3) Построение
верхней огибающей. Построим
на координатной плоскости
![]() все три прямых, а затем и их верхнюю
огибающую (рис. 13).
все три прямых, а затем и их верхнюю
огибающую (рис. 13).
4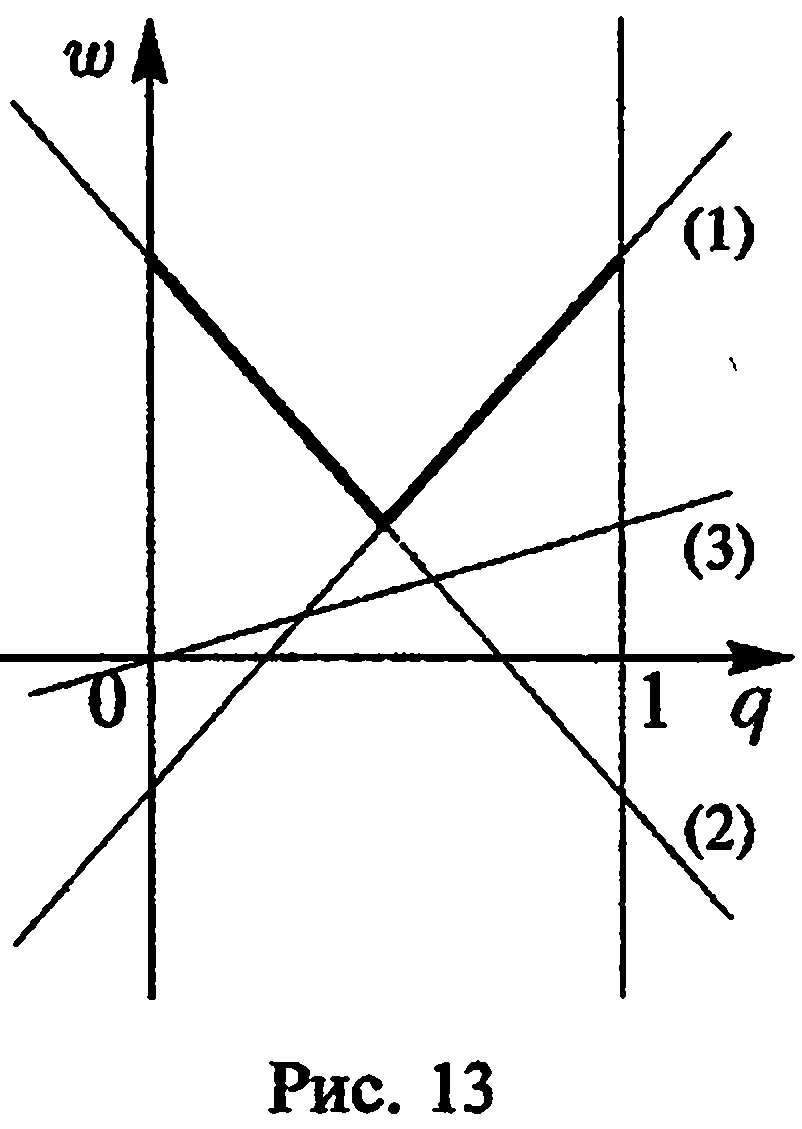
 )
Отыскание цены игры и оптимальной
смешаннойcстратегии
игрока В. Нижняя
точка верхней огибающей является точкой
пересечения прямых (1) и (2). Решая систему
уравнений
)
Отыскание цены игры и оптимальной
смешаннойcстратегии
игрока В. Нижняя
точка верхней огибающей является точкой
пересечения прямых (1) и (2). Решая систему
уравнений
![]()
![]() получаем
получаем
![]()
5) Отыскание
оптимальной смешанной стратегии игрока
А. Полагая
![]()
![]()
![]() приравниваем
средние выигрыши игрока А,
соответствующие
чистым стратегиям игрока В,
приравниваем
средние выигрыши игрока А,
соответствующие
чистым стратегиям игрока В,
![]() и находим
и находим
![]() .
Таким образом, цена игры и оптимальные
смешанные стратегии игроковА
и В
соответственно
равны
.
Таким образом, цена игры и оптимальные
смешанные стратегии игроковА
и В
соответственно
равны
![]() .
.
m![]() n
игры.
n
игры.
Решение любой матричной игры может быть найдено методами линейного программирования. При этом требуемый объем вычислений напрямую зависит от числа чистых стратегий игроков (растет с его увеличением и, значит, с увеличением размеров матрицы игры). Поэтому любые приемы предварительного анализа игры, позволяющие уменьшать размеры ее платежной матрицы или еще как-то упрощать эту матрицу, не нанося ущерба решению, играют на практике весьма важную роль. Правило доминирования.
В целом ряде случаев анализ платежкой матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров.
Опишем одну из таких возможностей более подробно.
Пусть А=
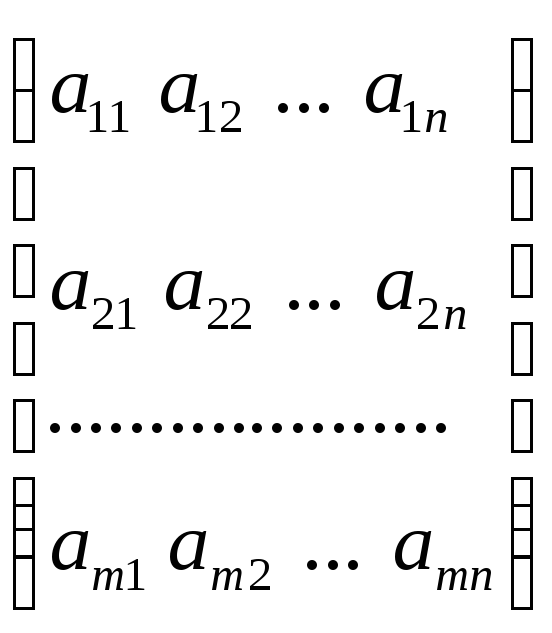 -произвольная
m
-произвольная
m![]() n
- матрица.
Будем говорить, что
i-я строка
матрицы А
n
- матрица.
Будем говорить, что
i-я строка
матрицы А
![]() не больше j
-й строки
этой матрицы
не больше j
-й строки
этой матрицы
![]() ,
если одновременно выполнены следующиеn
неравенств
,
если одновременно выполнены следующиеn
неравенств
![]() .
При этом говорят также,что
j-я
строка доминирует
i-ю строку,
или что стратегия
А
.
При этом говорят также,что
j-я
строка доминирует
i-ю строку,
или что стратегия
А![]() игрока А
доминирует
стратегию А
игрока А
доминирует
стратегию А![]() .
.
Замечание. Игрок А поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые строки.
Если в матрице А одна из строк (j -я) доминирует другую строку (i-ю), то число строк в матрице А можно уменьшить путем отбрасывания доминируемой строки (i-й).
Аналогично, можно
определять
l-й
столбец доминирующий
k-й
столбец, или что стратегия В![]() игрока В
доминирует
стратегию В
игрока В
доминирует
стратегию В![]() .
При этомразличие
бкдет только в знаках неравенств, то
есть для k-го
столбца
.
При этомразличие
бкдет только в знаках неравенств, то
есть для k-го
столбца
![]() меньшего
l-го
столбца
меньшего
l-го
столбца
![]() неравенства примут вид:
неравенства примут вид:
![]() .
.
Замечание. Игрок В поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые столбцы.
Если в матрице А один из столбцов (l-й) доминирует другой столбец (k-й), то число столбцов в матрице А можно уменьшить путем отбрасывания домииируемого столбца (k-го). Замечание. Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре: доминируемые чистые стратегии игроков в смешении не участвуют - соответствующие им вероятности следует взять равными пулю. Пример 7. Рассмотрим игру с матрицей
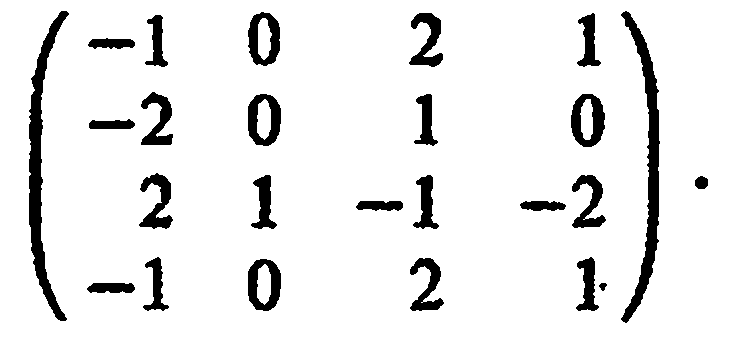
Сравнивая строки
матрицы, видим, что
1-я строка совпадает
с 4-й строкой, или, что то же, стратегия
А![]() дублирует стратегию А
дублирует стратегию А![]() .
Значит, одну из этих строк можно
вычеркнуть, не нанося ущерба решению
.
Значит, одну из этих строк можно
вычеркнуть, не нанося ущерба решению
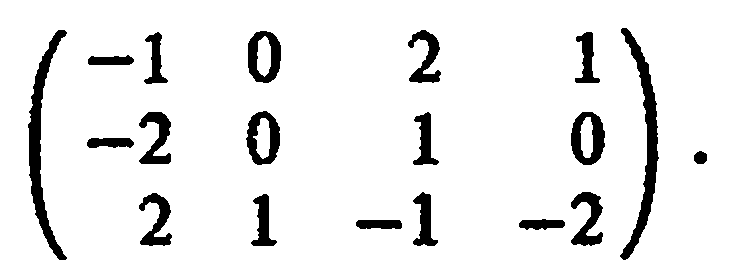
Поэлементно
сравнивая 1-ю и 2-ю строки, замечаем, что
1-я строка
доминирует
2-ю строку, или, что то же, стратегия А![]() доминирует
стратегию А
доминирует
стратегию А![]() .Это вновь
позволяет уменьшить число строк
матрицы
.Это вновь
позволяет уменьшить число строк
матрицы
![]()
Замечая, что 4-й столбец полученной матрицы доминирует ее 3-й столбец, и вычеркивая его, приходим к игре с 2 х 3-матрицей
![]()
Решая эту
2 х 3 игру
графическим методом, находим ее решение
- цену игры и
оптимальные смешанные
стратегии игроков А
и В:
v
= 0,
![]()
Возвращаясь к
исходной 4 х 4 игре, получаем окончательный
ответ:
v
= 0,
![]()
Замечание. При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усеченной матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий. Аффинное правило.
При поиске решения матричных игр часто оказывается полезным следующее свойство.
Допустимые
преобразования матрицы игры и ее цена.
Оптимальные
стратегии у матричных игр, элементы
матриц А и
С которых
связаны равенствами
![]() i=1,2,…,m;
k=1,2,…,n,
где λ>0,а µ -
произвольно,
имеют одинаковые равновесные ситуации
(либо в чистых, либо в смешанных
стратегиях), а их цены удовлетворяют
следующему условию
i=1,2,…,m;
k=1,2,…,n,
где λ>0,а µ -
произвольно,
имеют одинаковые равновесные ситуации
(либо в чистых, либо в смешанных
стратегиях), а их цены удовлетворяют
следующему условию
![]()
Пример 8. Элементы матриц
![]()
связаны
равенством
![]() i=1,2;
k=1,2,3.
Поэтому цена
игры с матрицей С легко вычисляется
i=1,2;
k=1,2,3.
Поэтому цена
игры с матрицей С легко вычисляется
![]() (см. пример 7).
(см. пример 7).
Основные этапы поиска решения матричной игры.
1-й этап - проверка наличия (или отсутствия) равновесия в чистых стратегиях (при наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры).
2-й этап - поиск доминирующих стратегий (в случае успеха этого поиска - отбрасывание доминируемых строк и столбцов в исходной матрице игры).
3-й этап - замена игры на ее смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.
