Лекция №9. Сплайн-интерполяция

Лекция № 9.

Интерполирование сплайнами

Построение интерполяционного многочлена Лагранжа и Ньютона с использованием большого числа узлов интерполирование на отрезке [a, b] может привести к плохому приближению интерполируемой функции из-за возрастания вычислительной погрешности. Такой интерполяционный многочлен существенно проявляет свои колебательные свойства, и его значения между узлами могут значительно отличаться от значений интерполируемой функции.

Кроме того, построенный многочлен будет иметь высокую степень, что тоже весьма нежелательно. Этих неприятностей можно избежать, разбив отрезок [a, b] на частичные отрезки и построив на каждом из них многочлен невысокой степени, так или иначе приближенный к заданной функции f(x).

Одна из возможностей преодоления этого недостатка заключается в применении сплайн-интерполяции. Иногда такой прием называют кусочно-полиномиальным интерполированием.

Суть сплайн-интерполяции заключается в определении интерполирующей функции по формулам одного типа для различных подмножеств и в стыковке значений функции и ее производных на границах подмножеств.

Наиболее изученным и широко применяемым является вариант, в котором между любыми двумя точками строится многочлен п-й степени.

,

который в узлах интерполяции принимает значения интерполируемой функции и непрерывен вместе со своими (п-1)-й производными. Такой кусочно-непрерывный интерполяционный многочлен называется сплайном.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разница между степенью сплайна и порядком наивысшей непрерывной производной – дефектом сплайна.

Одним из наиболее распространенных интерполяционных сплайнов является кубический сплайн. Для вывода кубического интерполяционного сплайна воспользуемся его интерпретацией как гибкой линейки, изогнутой таким образом, что она проходит через значения функции в узлах, т.е. является упругим бруском в состоянии свободного равновесия.

Определение кубического сплайна.

Пусть на отрезке [a, b] задана функция y = f(x). Рассмотрим сетку узлов

a=x₀ < x₁ <x₂ < … < x_n = b (1)

и обозначим расстояние между смежными узлами:

h_i = x_i – x_i-1, i=1, 2, …, n (2)

определение. Назовем кубическим сплайном функции y = f(x), х  [a; b] на сетке (2) функцию S(x), удовлетворяющую условиям:

1. На каждом частичном отрезке [x_i-1; x_i] функция S(x) является полиномом третьей степени.

2. Функция, ее первая S'(x) и вторая S''(x) производные непрерывны на сегменте [a; b].

3. В узлах интерполяции сплайн принимает значения интерполируемой функции:

S(x_i) = f(x_i) = f_i, i=0, 1, 2, …, n.

4. На концах сегмента [a; b] вторая производная функции S''(x) удовлетворяет условиям S''(а)= S''(b)=0.

Замечание. На концах сегмента [a; b], в принципе, могут быть заданы и другие условия, например, S''(а)=А, S''(b)=В.

Справедлива следующая теорема.

Теорема. Существует единственный сплайн S(x), удовлетворяющий условиям 1-4.

Проведем доказательство теоремы конструктивным способом, т.е. сведем задачу построения сплайна к определению коэффициентов частичных полиномов третьей степени на каждом из отрезков [x_i-1; x_i]. Для этого сопоставим отрезку [x_i-1; x_i] полином S_i (x).

Запишем полином S_i (x) в виде:

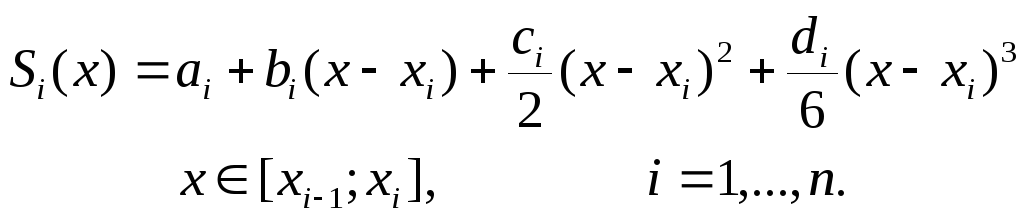(3)

При этом очевидно, что

(4)

(5)

Подставив x_i в (3), (4), (5), получим:

, , (6)

Отсюда следует, что для выполнения условия 3 в узлах интерполяции

: , i= 1, 2, …, n (7)

Требуя непрерывности сплайна в узлах x_i , i= 1, 2, …, n-1 и выполнения условия 3 при i=0, получаем:

, i= 1, 2, …, n (8)

или

Это равенство можно переписать следующим образом:

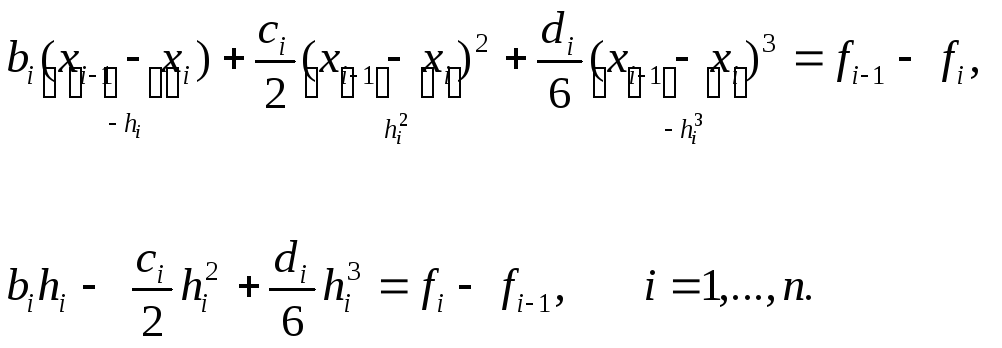(9)

Условие 2 относительно непрерывности первой производной S'(x) в узлах x_i, i = 1, … n-1, принимает вид:

(10)

и приводит к соотношениям

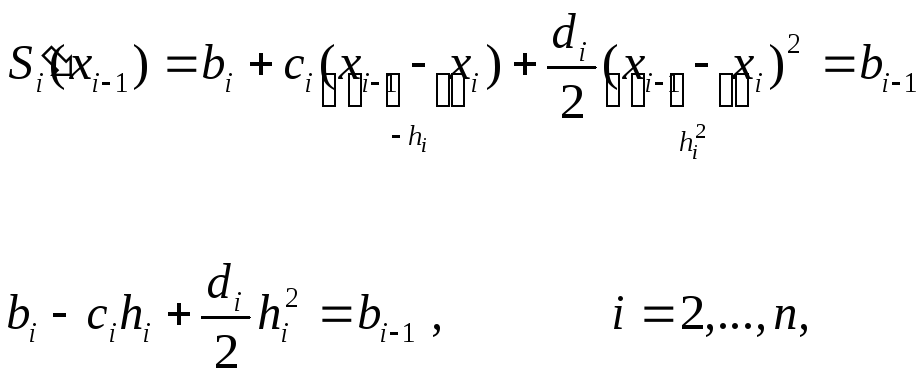
или

(11)

Аналогичным образом условия непрерывности второй производной S'' (x) в тех же узлах

(12)

означают, что

(13)

Наконец, дополнительные граничные условия 4 дают еще два уравнения:

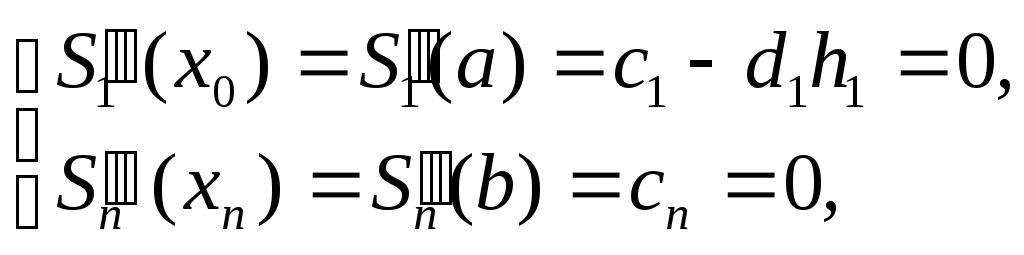(14)

В итоге мы получили замкнутую систему (9), (11), (13), (14), содержащую в сумме 3п линейных уравнений для отыскания 3п неизвестных: b_i, с_i , d_i, i=1,2,…, n.

Удобно формально ввести еще одно неизвестное с₀, положив при этом что оно равно нулю: с₀ = 0, и первое уравнение в (14) переписать в виде

,

т.е. в форме, аналогичной (13).

Теперь уравнения (13), (14) естественно представить в единообразном виде:

(15)

(16)

Обратим внимание на то, что из системы (15) можно выразить все коэффициенты d_i через разности , а затем из системы (9) выразить через c_i и c_i-1 все коэффициенты b_i. Подставляя полученные выражения в (11), приходим к системе линейных уравнений для c_i:

(17)

Сдвигая индекс i на единицу, получаем симметрическую форму записи уравнений (17):

(18)

Кроме того, согласно (16)

с₀ = с_п = 0 (19)

Система (18) содержит (п-1) уравнение с (п-1)-м неизвестным:

с₁, с₂, …, с_п-1.

Величины с₀ и с_п определены дополнительными соотношениями (19). Если сетка (1) равномерная, т.е. h_i=h=const, то уравнения (18) принимают особенно простой вид:

(20)

Для уравнений системы (18) выполнено условие диагонального преобладания. Отсюда следует существование и единственность решения задачи (18), (19). Зная величины c_i, можно рассчитать остальные коэффициенты сплайна по формулам

(21)

(22)

завершив тем самым построение сплайна. Теорема доказана.

Замечание о решении системы

Уравнения (18) имеют так называемую трехточечную структуру. Такие системы имеют следующий вид:

(23)

y₀=0, y_n=0 (24)

соответствует системе линейных уравнений с трехдиагональной матрицей Т для определения вектора неизвестных у =(у₁, у₂, …, у_п-1):

Ту=F,

где

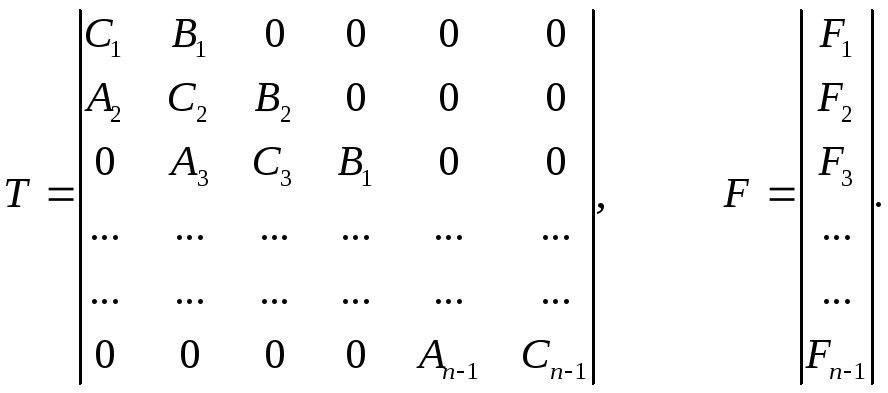(25)

При этом легко видеть, что в нашем случае

(26)

поскольку

(27)

решение таких систем эффективно решается с помощью методов прогонки.

Пример.

Для функции y=f(x)=3^x на отрезке [-1; 1] с узлами интерполяции х₀=-1, х₁=0, х₂=1. Построить кубический сплайн.

Найти его значение при х=1/2 (т.е. приближенно ). Определить погрешность сплайна.

Решение. В данном случае имеем равномерную сетку с шагом h=1. на сетке одна внутренняя точка – х₁ и две граничные: х₀ и х₂. система (20) сводится к одному уравнению относительно коэффициента с₁, которое с учетом дополнительных соотношений (16), определяющих нулевые значения коэффициентов с₀ и с₂, принимает вид:

таким образом, с₀=0, с₁=2 и с₂=0. Остальные коэффициенты сплайна определим из формул (7), (21), (22): а₁=1, а₂=3, d₁=2, d₂=-2, b₁=4/3, b₂=7/3.

Теперь можно выписать кубические полиномы, определяющие сплайн:

Легко проверить, что построенная таким образом функция S(x) непрерывна вместе с первой и второй производной во внутренней узловой точке х=0.

Вычислим значение сплайна в точке х=1/2, т.е посчитаем приближенное значение :

Значительная погрешность обусловлена, прежде всего, большим шагом h=1. определенную роль играют условия (4):

(*).

Вторая производная рассматриваемой функции f(x)=3^x в точках х=±1 в ноль не обращается, т.е. условие (*) дает о ней искаженную информацию. Если при построении сплайна учесть истинные значения вторых производных в граничных точках, то точность аппроксимации улучшится.

6