Интерполирование, интерполяционные многочлены Лагранжа и Ньютона.

1. Общая постановка задачи об интерполировании. Параболическое интерполирование.

При решении многих задач используются функции, заданные таблицей. Например, если опытным путем найдем ряд значений некоторой функции, то для вычисления тех значений, которые не содержатся в таблице, можно подобрать другую, более простую функцию, в некотором смысле близкую данной.

Существуют разные способы получения таких функций. Один из них – интерполирование.

В общем виде задача интерполирования формулируется так:

Пусть n+1 в точках

х₀, х₁, х₂, …, х_n

заданы значения функции

y = f(х): f(х₀) = y₀, f(х₁) = y₁, ..., f(х_n) = y_n.

Требуется подобрать достаточно простую функцию φ(х), удовлетворяющую следующим условиям:

а) в точках х₀, х₁, х₂, …, х_n значения функции должны совпадать со значениями данной функции f(х):

φ(х_k) = f(x_k) = y_k (k = 0, 1,2,…,n); (1)

б) при остальных значениях х из области определения должно выполняться приближенное равенство

f(x)  φ(х) (2)

Функция φ(х) называется интерполирующей,

процесс ее построения – интерполированием,

а точки х₀, х₁, х₂, …, х_n, в которых значения интерполирующей функции должны совпадать с заданными значениями данной функции, - узлами интерполирования.

Точка х, в которой вычисляется значение функции f(x) с помощью функции φ(х), называется точкой интерполяции.

Если x[x₀; x_n], то процесс нахождения называется интерполяцией, иначе – экстраполяцией.

Параболическое интерполирование. Интерполирующая функция обычно подбирается из определенного класса функций. Часто в качестве такой функции берется многочлен F_n(x), который называется интерполяционным многочленом.

Интерполирование при помощи многочлена называется параболическим интерполированием, геометрический смысл которого состоит в том, что график данной функции f(x) заменяется параболой-графиком многочлена F_n(x); при этом графики имеют n+1 общую точку.

Итак, задача параболического интерполирования формулируется следующим образом:

Пусть значения функции f(х) заданы в п + 1 узле интерполирования

х₀, х₁, х₂, …, х_n, причем

f(х₀) = y₀, f(х₁) = y₁, ..., f(х_n) = y_n.

В качестве интерполирующей функции выберем многочлен

F_п(х) = с₀ xⁿ+ с₁х^n-1 + ... + с_n-1х +c_n (3)

и потребуем, чтобы в узлах интерполирования значения интерполяционного многочлена совпадали со значениями данной функции:

F_n(х_k)= y_k (k=0, 1,2, …, n). (4)

Для вычисления неизвестных коэффициентов многочлена на основании условия (4) составим систему уравнений:

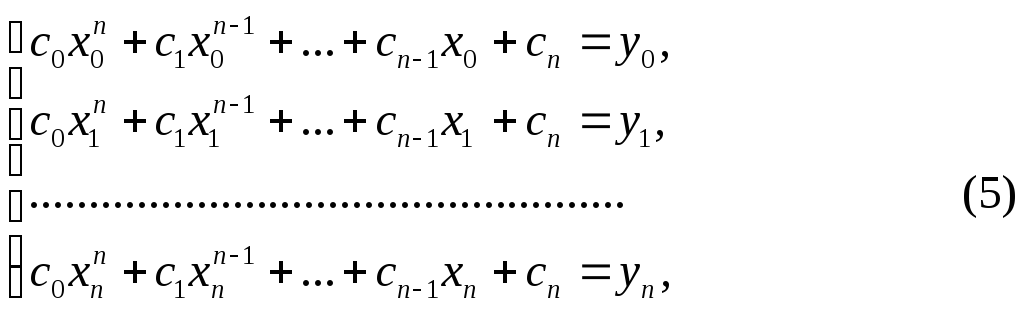
Система (5) состоит из n + 1 уравнения; переменными считаются числа c₀, c₁, …,c_n.

Составим определитель системы (5):

Этот определитель известен из курса высшей алгебры как определитель Вандермонда.

Поскольку узлы интерполирования х₀, х₁, х₂, …, х_n различны, то   0, следовательно, линейная система (5) имеет единственное решение, что означает существование и единственность интерполяционного многочлена F_n(х).

Следует заметить, что при решении различных задач используются различные записи интерполяционного многочлена.

Интерполяционный полином Лагранжа

Согласно условий (1), (2), предъявляемых к функции φ(х), запишем многочлен n-ой степени.

_n

φ(х)≡F_n(x) = ∑ f(x_i) p_i(x) (6)

ⁱ⁼⁰

В узле x_i многочлен (6) на основании (1) должен принимать значение f_i. Значит, сомножитель p_i(x) в точке x_i должен быть равен 1,т.е.

p_i (x_i) = 1.

В то же время другие слагаемые многочлена (6) должны быть равны нулю, т.е.

p_k (x_i) = 0, i ≠ k, i, k = 0, 1, …,n.

Таким образом, мы сформулировали требования к сомножителю p_i(x) , а именно:

p_i (x_i) = 1 , i = 0, 1, …,n (7)

p_k (x_i) = 0, i ≠ k; i, k = 0, 1, …,n. (8)

Сомножитель p_i(x) называют вспомогательным многочленом степени n.

Учитывая свойство (8) и требование, чтобы многочлен p_i(x) имел степень n, запишем:

p_i(x) = c_i (x-x₀) (x-x₁)… (x-x_i-1) (x-x_i+1) (x-x_i+2)… (x-x_n) (9)

где c_i некоторый коэффициент.

При x = x₀, x₁,… x_i-1, x_i+1, … x_n

p_i(x) = 0.

Для определения c_i обратимся к требованию (7). Из него следует:

p_i(x_i) = c_i (x_i-x₀) (x_i-x₁)… (x_i-x_i-1) (x_i-x_i+1) (x_i-x_i+2)… (x_i-x_n) = 1

Тогда

c_i = (10)

Сделав подстановку (10) в (9), получим окончательное выражение для p_i(x):

p_i(x) = (11)

Построенный многочлен (11), например, в точке x₀ принимает значение p₀(x₀) = 1, а в остальных узлах – значения, равные нулю.

Многочлен p₁(x) в точке x₁ будет равен 1, а в остальных узлах обращается в 0, и т.д.

Таким образом, вспомогательный многочлен p_i(x) полностью удовлетворяет требованиям (7), (8), а многочлен n-ой степени

_n

F_n(x) = ∑ f(x_i) p_i(x)

ⁱ⁼⁰

является интерполяционным многочленом Лагранжа.

Замечание: многочлен Лагранжа целесообразнее использовать в задачах восстановления функции f(x) , когда точка интерполяции x расположена ближе к центру сетки.

Тестирование алгоритма

Рассмотрим функцию f(x), заданную таблицей:

xi	1	2	4	5
fi	2	1	2	3

Построим многочлен Лагранжа для этой функции.

F₃(x) = 2 + 1 + 2 +3

Если вместо x подставить 1, то F_n(1)= f₁ = 2,

при x = 4 F_n(4)= f₃ = 2 и т.д.

Следовательно, построенный многочлен удовлетворяет главному условию (1).

Таким образом, тестирование алгоритма будет состоять в следующем:

1. задать поочередно в качестве точек интерполяции табличные значения x_i и получить соответствующие значения функции f_i (при правильно работающей программе должно выполняться условие (1)).

2. задать в качестве точек интерполяции несколько значений, не являющихся узлами сетки, и проверить выполнение условия (2).

Оценка погрешности интерполяционной формулы Лагранжа

Пусть:

f(x) – F_n(x) = R_n(x),

тогда

f(x) = F_n(x) + R_n(x), (12)

Разность R_n(x) называется остаточным членом формулы Лагранжа. Значение R_n(x) равно погрешности, которая получается при замене значения функции f(x) значением интерполяционного многочлена F_n(x).

Если предположить, что функция f(x) имеет на отрезке [a, b]

(a = min {x_k}; b = max {x_k}) производные до порядка n+1,

^{k k}

то для остаточного члена можно получить формулу

R_n(x) = f⁽ⁿ⁺¹⁾(ξ) (13)

где точка ξ  [a, b] и зависит от точки х.

Формулу (13) можно записать иначе:

R_n(x) =_n+1 (x). (14)

Если

max |f⁽ⁿ⁺¹⁾ (x)|  M_n+1

^{x  [a; b]}

то получим оценку остаточного члена:

|R_n(x)|  |_n+1 (x)|. (15)

Пример. Для функции у= 2^х построим интерполяционный многочлен Лагранжа, выбрав узлами интерполирования точки

x₀ = - 1, x₁ = 0, x₂ = 1, x₃ = 2.

Вычислим соответствующие значения функции:

у₀= ½ , у₁=1, у₂=2, у₃=4;

по формуле Лагранжа найдем:

F₃(x) =x³ + x² +x+1.

Оценим погрешность, которая получается при замене функции у= 2^х многочленом F₃(x). Производная четвертого порядка

F⁽⁴⁾(x) = 2^x(ln 2)⁴.

На отрезке [-1; 2] функция 2^x возрастает, поэтому 0< 2^x <= 4.

M₄ = 4 (ln 2)⁴, ln 2 = 0,693…<, поэтому M₄ < 4 = 1.

₄ (х) = x (x + 1)(x - 1)(x –2).

По формуле (15) получим:

Многочлен Ньютона

Рассмотренный многочлен Лагранжа, как правило, используется в задачах восстановления функции f(x), когда точка интерполяции х находится ближе к центру сетки.

Если же точка интерполяции х расположена ближе к краям сетки, целесообразнее использовать многочлен Ньютона. Здесь возможны два случая:

1. точка интерполяции х находится вблизи первого узла сетки х₀ (полином Ньютона I);

2. точка интерполяции х находится вблизи последнего узла сетки х_n (полином Ньютона II).

Замечание. Построение многочлена Лагранжа основывается на вспомогательном многочлене p_i(x).

В основе же построения многочлена Ньютона находится понятие конечной разности.

Определим понятие конечной разности.

Пусть функция задана таблицей с постоянным шагом h:

хi	х0	х1	…	хi	…	хn
уi	у0	у1	…	уi	…	уn

где х_i = х₀ + ih (i = 0, 1, …,n).

Тогда конечными или табличными разностями первого порядка или первыми разностями называются числа, равные приращениям значений функции

у₀ =у₁ – у₀ = f(x₁) – f(х₀);

у₁ =у₂ – у₁ = f(x₂) – f(х₁);

… … …

у_n-1 =у_n – у_n-1 = f(x_n) – f(х_n-1).

Приращения разностей первого порядка называются разностями второго порядка:

²у₀ =у₁ – у₀ ,

²у₁ =у₂ – у_1.

Вообще разности любого порядка k определяются равенствами

^kу_m =^{k - 1}у_{m +1} – ^{k - 1}у_m.

Будем считать, что ⁰у_m = у_m.

Последовательно получаемые разности удобно записывать в форме таблицы:

хi	уi	уi	^2уi	^3уi	…
х0	у0
		 у0
х1	у1		^2 у0
		у1		^3 у0
х2	у2		^2 у1
		у2
х3	у3
…	…

Пример. Построим таблицу конечных разностей для функции

y = cosx на отрезке [0; 0,7] с шагом h = 0,1.

Таблица будет иметь вид:

хi	уi 10^5	уi 10^5	^2уi10^5	^3уi10^5	^4уi10^5	^5уi10^5
0,0	1,00000
		-500 ( у0)
0,1	0,99500		-993 (^2 у0)
		-1493 (у1)		+13 (^3 у0)
0,2	0,98007		-980 (^2 у1)		+12
		-2473 (у2)		25 (^3 у1)		-2
0,3	0,95534		-950 (^2 у2)		+10
		-3428 (у3)		35 (^3 у2)		-1
0,4	0,92106		-920 (^2 у3)		+9
		-4348 (у4)		44 (^3 у3)		-3
0,5	0,87758		-876 (^2 у4)		+6
		-5224 (у5)		50 (^3 у4)
0,6	0,82534		-826 (^2 у5)
		-6050 (у6)
0,7	0,76484

Первая интерполяционная формула Ньютона

Пусть функция у = f(x) задана значениями в n+1 равноотстоящем узле. Будем искать выражение интерполяционного многочлена в виде:

P_n (х) = а₀ + а₁ (х – х₀ ) + …+ а_n (х – х₀ )(х – х₁ )… (х – х_n-1) (1)

при этом потребуем, чтобы выполнялись условия:

P_n (х_i) = f(х_i) (i = 0,1, …,n), (2)

т.е. потребуем, чтобы значения многочлена и функции в узлах интерполирования совпадали.

Для определения коэффициентов многочлена (1) используем условия (2).

При х = х₀ P_n (х₀ ) = а₀ = у₀  а₀ = у₀

При х = х₁ P_n (х₁ ) = а₀ + а₁ (х₁ – х₀ ) = у₁ 

у₁ = а₀ + а₁ h  а₁ =

а₁=

При х = х₂

P_n (х₂ ) = а₀ + а₁ (х₂ – х₀ )+ а₂ (х₂ – х₀ )(х₂ – х₁) = у₂ 

у₂ = а₀ + а₁ (х₂ –х₀) + а₂ (х₂ – х₀ )(х₂ – х₁) =

= у₀ + (х₀ +2h – х₀) + а₂(х₀ +2h – х₀) h = у₀ +2у₀ + 2 h² а₂

С другой стороны

у₂ = у₁ + у₁ = у₀ + у₀ + у₁ = у₀ + у₀ + у₁ - у₀ + у₀ = у₀ + 2у₀+ ²у₀.

Тогда

у₀ +2у₀ + 2 h² а₂ = у₀ + 2у₀+ ²у₀ 

а₂ =

Аналогично, при х = х₃ получим а₃ =

и вообще

а_k = (k = 0, 1, …, n)

Подставив найденные значения коэффициентов в (1), получим

P_n (х) = у₀ + (х – х₀ ) + (х – х₀ )(х – х₁ )+ …

+ (х – х₀ )(х – х₁ )… (х – х_n-1)

Этот многочлен и называется первым интерполяционным многочленом Ньютона.

В силу единственности интерполяционного многочлена для всех х  [х₀ ; х_n] P_n(x)  F_n(x), и поэтому остаточный член формулы Ньютона можно записать в виде:

R_n(x) =_n+1 (x),

где _n+1 (x)= (х – х₀ )(х – х₁ )… (х – х_n)

На практике иногда удобнее пользоваться другой формулой записи многочлена Ньютона.

Положим t =  = t – 1; = t – 2;…; = t – n +1

 P_n (х) = P_n (х₀ + ht) = у₀ +tу₀ + ² у₀ + …+ ⁿ у₀

Остаточный член в этом случае находится по формуле:

R_n(x) = f⁽ⁿ⁺¹⁾(ξ) hⁿ⁺¹,

и абсолютную погрешность формулы можно оценить с помощью неравенства

/R_n(x)/  /t(t - 1)(t - 2)…(t - n)/ M_n+1

Замечание. Очевидно t = представляет собой число шагов, необходимых для достижения точки х, исходя из точки х₀.

Первую интерполяционную формулу Ньютона целесообразно использовать для интерполирования функции у = f(x) в окрестности начального значения х₀ , где t мало по абсолютной величине.

Первую интерполяционную формулу Ньютона обычно называют формулой "интерполирования вперед".

Если требуется найти значение функции f(x) при х = х^*, то в качестве х₀ выбирается ближайшее, меньшее х^* значение аргумента.

Пример. Найти cos 0,05 по данным, приведенным в таблице конечных разностей и оценить погрешность.

Запишем многочлен Ньютона третьего порядка.

P₃ (х) = у₀ +tу₀ + ² у₀ + ³ у₀ ,

Возьмем х₀ = 0,0  t == = 0,5.

Подставляя значения t и разностей в выражение P₃ (х) получим:

P₃ (0,05) = 1,0 +0,5 (-0,005) + (-0,00993) + 0,00013  0,99875;

Производная f ⁴(x) = cosx и M₄ = cos0 = 1. Абсолютная погрешность оценивается так:

/R_n(0,05)/  |0,5(- 0,5)(- 1,5)(-2,5) | < 4*10^-6

Значит, все цифры полученного результата будут верными.