лекция №12 Эмпирические формулы

Лекция

Обработка результатов наблюдений

Составление эмпирических формул

Постановка задачи о составлении эмпирических формул. Графическое решение.

При эмпирическом определении зависимостей между величинами составляется таблица по опытным данным, в соответствии с которой подбирается формула, приближенно выражающая исследуемую зависимость, т.е. подбирается функция хорошо изученного класса, значения которой близки к значениям, найденным опытным путем. Полученная таким образом формула называется эмпирической.

Пусть в результате опыта получены значения у₁, у_2, …,у_п величины у, соответствующие значениям х₁, х_2, …, х_п другой величины х. Эти данные следует занести в таблицу:

х1	х2	…	…	хп
у1	у2	…	…	уп

Совокупность точек М_k (x_k, y_k) (k=1, 2,…,n), называемых опытными точками, позволяет строить точечный график.

На первый взгляд самым естественным путем кажется отыскание многочлена у(х), принимающего в точках х₁, х_2, …,х_п значения, равные у₁, у_2, …,у_п. Однако, даже если истинная зависимость выражается простой гладкой кривой (пунктир), точки, найденные экспериментально, отклоняются от нее в силу неизбежных случайных ошибок измерения. Поэтому нет необходимости искать эмпирическую функцию, график которой проходил бы точно через опытные точки.

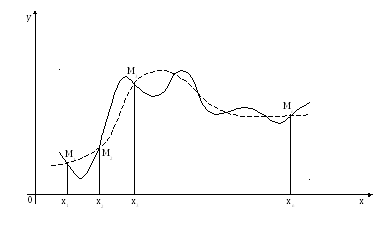
Искомую плавную линию рекомендуется проводить так, чтобы опытные точки располагались достаточно близко и по обе стороны от нее.

Если удастся составить уравнение полученной линии, то тем самым будет получена искомая эмпирическая формула. В эту формулу обычно входят один и более параметров, которые необходимо определить.

Метод наименьших квадратов

Общая характеристика метода наименьших квадратов

Пусть зависимость между х и у выражается формулой определенного вида с несколькими параметрами a, b, c,…, т.е. пусть y = φ(х, a, b, c,…).

Соответствующее значение эмпирической функции в точке x_i (i=1, 2,…, n) обозначим . Подберем параметры эмпирической формулы так, чтобы расстояние между точками (у₁, у_2, …,у_п,) и () было наименьшим:

наименьшее значение примет тогда и функция

(1)

такой способ подбора параметров носит название метода наименьших квадратов.

Для определенности рассмотрим случай трех параметров a, b, c. Подберем a, b, c так, чтобы функция F (a, b, c) приняла наименьшее значение внутри рассматриваемой области. В последнем случае в силу необходимого условия экстремума в этой точке должны выполняться следующие соотношения:

(2)

С учетом (1) условия (2) можно записать так:

(3)

где частные производные вычислены в точке x_i (i=1, 2,…,n). Получили систему трех уравнений с тремя переменными a, b, c, решая которую найдем параметры a*, b*, c*. Искомая эмпирическая формула примет следующий вид:

y =f(x, a^*, b^*, c^*).

Линейная зависимость

Эмпирическая формула y = ax + b содержит два параметра a и b.

При определении параметров по методу наименьших квадратов система (3) примет вид:

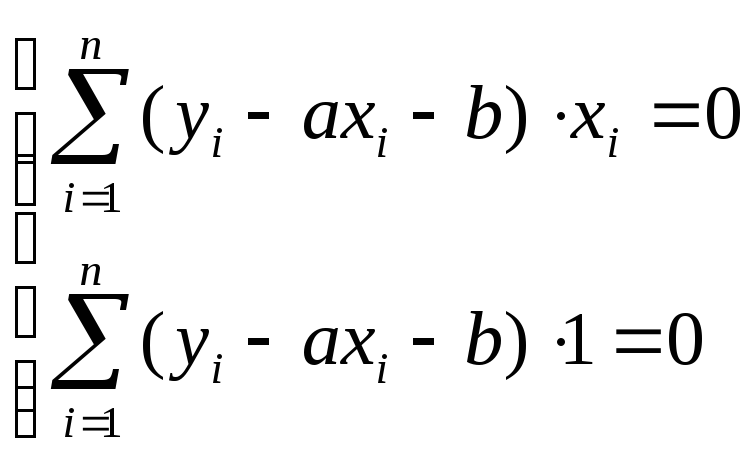
Выполнив все необходимые преобразования, получим:

(4)

где

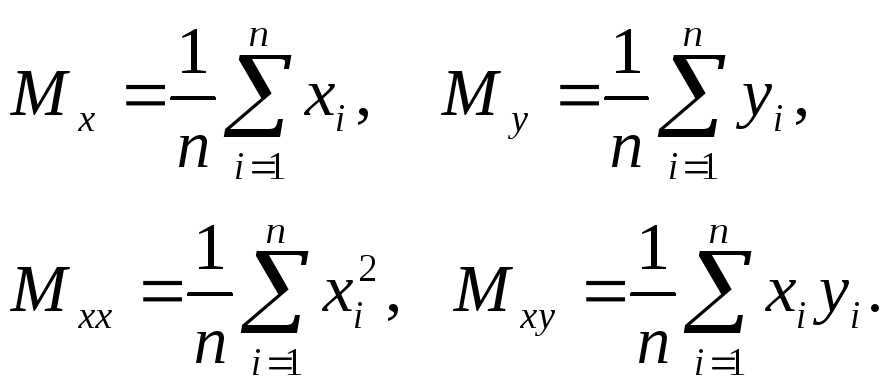(5)

Пример. Пусть изучается зависимость растворимости S азотнонатриевой соли от температуры t. Ставится эксперимент, результаты изменений заносятся в таблицу:

t, ºC	0	4	10	15	21	29	36	51	68
S	66,7	71,0	76,3	80,6	85,7	92,9	99,4	113,6	125,1

Построение опытных точек показывает, что они близки к некоторой прямой. Следовательно, необходимо найти линейную эмпирическую формулу:

Для определения параметров a, b используем метод наименьших квадратов и составим таблицу:

Результаты измерений			Вычисление коэффициентов системы		Оценка точности формулы S=at+b
k	tkº	Sk	Sk tk	tk^2
	0	66,7	0	0	66,2	0,5
	4	71,0	284,0	16	69,9	1,1
	10	76,3	763,0	100	75,4	0,9
	15	80,6	1209,0	225	80,0	0,6
	21	85,7	1799,7	441	85,5	0,2
	29	92,9	2694,1	841	92,8	0,1
	36	99,4	3578,4	1296	99,2	0,2
	51	113,6	5793,6	2601	113,0	0,6
	68	125,1	8506,8	4624	128,6	-3,5
	234	811,3	24809,0	10144

M_tt= 10144/9=1127,111; M_t= 234/9=26 M_ts= 24809/9=2756,6 M_s= 811/9=90,1

Решая систему (4):

получим a=0,918; b=66,2.

Итак, .

Квадратичная зависимость.

Будем искать эмпирическую формулу вида:

Y = ax²+bx+c.

Система (3) для определения параметров a, b, c примет вид:

После ряда преобразований получим:

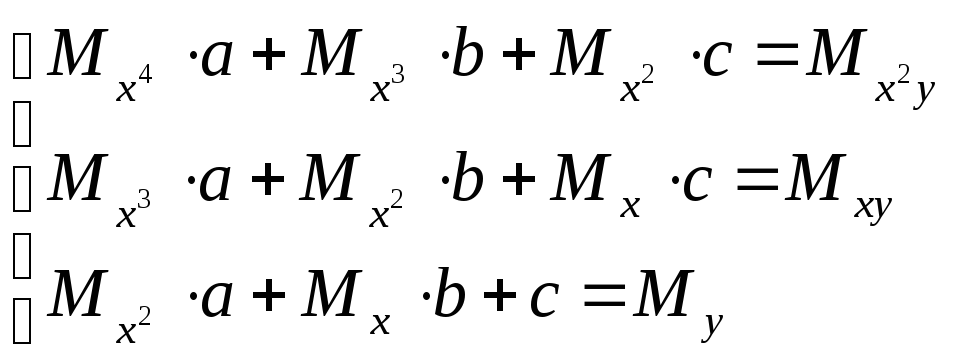(6)

где

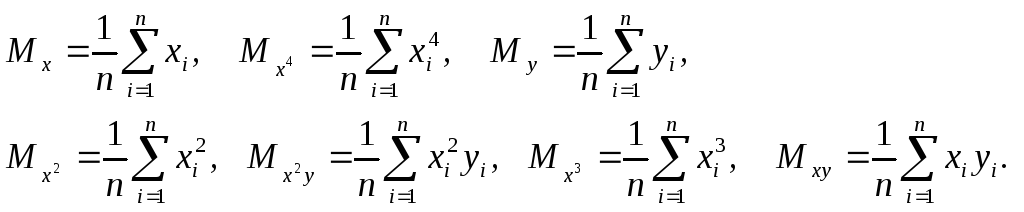(7)

Пример. Пусть функция задана таблицей:

x	0	2	4	5	8	10	12	15
y	29,8	22,9	17,1	15,1	10,7	10,1	10,6	15,2

Будем искать приближающую функцию в виде многочлена второй степени. Для нахождения параметров a, b, с составим систему вида (6), решая которую с учетом того, что

получим a=0,175; b=-3,618; c=29,276.

Итак, функция у на отрезке [0; 15] приближенно выражается многочленом

y = 0,175x² - 3,618x + 29,276.

Степенная и показательная зависимости.

В обоих случаях необходимо сначала перейти к соответствующей линейной зависимости и для нее определить параметры a, b по способу наименьших квадратов, поле чего следует возвратиться к первоначальным параметрам

5