ДМ_Конспект

для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Определение. Вершины и рѐбра графа называются также элементами
графа, число вершин в графе V – порядком, число рѐбер E – размером графа.
Определение. Вершины u и v называются концевыми вершинами (или
просто концами) ребра	e {u,v}.	Ребро, в	свою очередь, соединяет эти
вершины. Две концевые	вершины	одного	и того же ребра называются

соседними (смежными).

Определение. Два ребра называются смежными, если они имеют общую концевую вершину.

Таким образом, на множествах вершин V и ребер E неориентированного графа могут быть заданы отношения смежности.

Определение. Вершина называется инцидентной ребру, если она является его концевой вершиной.

Таким образом, на множествах вершин V и ребер E графа может быть задано отображение инцидентности.

Определение. Два ребра называются кратными, если множества их концевых вершин совпадают.

Определение. Ребро называется петлѐй, если его концы совпадают, то есть e {v,v}.

Определение. Степенью deg v (или (v) ) вершины v называют количество рѐбер, для которых она является концевой (при этом петли считают дважды).

Определение. Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом

ровно одного ребра.
Пример. На рисунке 18.1 порядок графа						V		6 (количество вершин),
размер графа		E		8 (количество ребер); 1 и	2 – смежные вершины (их

соединяет ребро a ); ребра a, b, e – смежные (имеют общую вершину 2); ребра

gи e – кратные (соединяют вершины 1 и 4); h – петля; 5 – висячая вершина; 6

–изолированная вершина. Степень вершины 2 – deg 2 3, степень вершины 4 – deg 4 5, степень вершины 1 – deg1 5 (петля считается 2 раза).

161

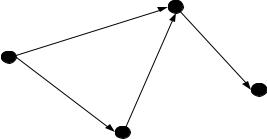
18.2 Ориентированный граф. Определения

Определение. Ориентированный граф (сокращѐнно орграф) G – это упорядоченная пара G : (V , A) , для которой выполнены следующие условия:

V это непустое множество вершин или узлов,

A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рѐбрами.

Определение. Дуга – это упорядоченная пара вершин (v, w) , где вершину

vназывают началом, а w – концом дуги.

В отличие от неориентированных графов, в ориентированных степень вершины определяется полустепенью захода и полустепенью исхода:

соответственно, deg v и deg v (рис. 18.2). Полустепень захода определяется количеством ребер, концом которых является данная вершина, полустепень исхода – количеством ребер, началом которых является вершина.

		2
		a
1		b
	d	c
		3

4

Рисунок 18.2 – Ориентированный граф

Пример. На		рис. 18.2 полустепени исхода			и захода вершин:
deg 1 2,	deg 1 0 ;	deg 2 1,	deg 2 2;	deg 3 0,	deg 3 1;
deg 4 1,	deg 4 1.
18.3 Основные термины для ориентированных и неориентированных
графов
Определение.		Смешанный граф G –		это граф,	в котором некоторые

рѐбра могут быть ориентированными, а некоторые – неориентированными (рис. 18.3) Записывается упорядоченной тройкой G : (V , E, A) , где V , E, A определены так же, как выше.

162

Ориентированный и неориентированный графы являются частными случаями смешанного.

	2
a
1	b
d	c
	3
4
Рисунок 18.3 – Смешанный граф
На рисунке 18.3 – ребра a и b	– неориентированные, дуги d	и	c –
ориентированные.
Определение. Подграфом графа G( X , E) называется граф G1 ( X1, E1 ) , все
вершины и дуги которого содержатся	среди вершин и дуг графа	G ,	т.е.

G1 G, X1 X , E1 E . Сам граф является своим подграфом.

Определение. Сам граф по отношению к своим подграфам называется

надграфом (или суперграфом).

Определение. Подграф называется собственным, если он отличен от самого графа.

Определение. Для любого подмножества S вершин графа G порождѐнным подграфом G называется максимальный подграф графа G , множеством вершин которого является S .

Определение. Часть графа, которая наряду с некоторым подмножеством ребер (дуг) графа содержит и все вершины исходного графа X1 X , E1 E называется суграфом.

Определение. Подграф G1 ( X1, E1 ) неориентированного графа G( X , E)

называется каркасом, или остовным деревом (остовом) графа G( X , E) , если

G1 – дерево и X1 X .

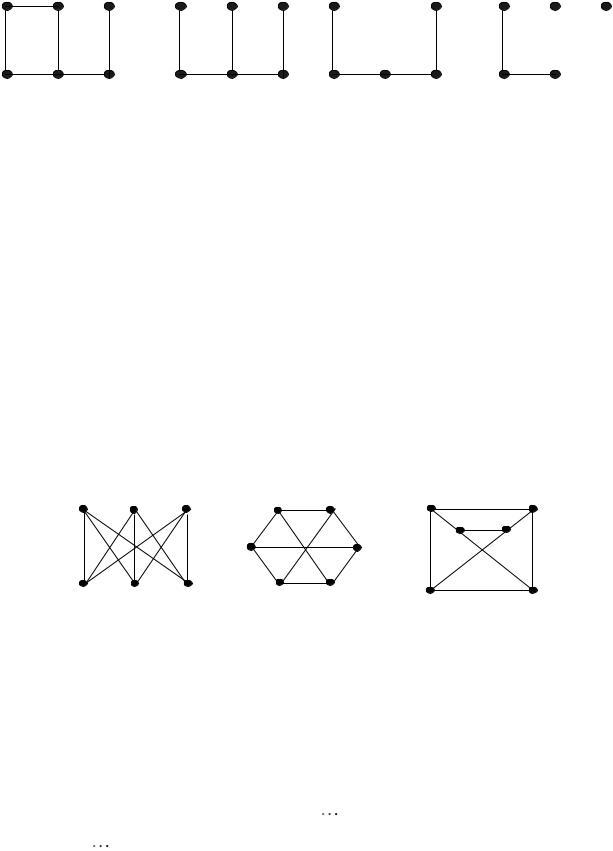
Пример. На рис. 18.4 изображен граф G и его подграфы. Подграф G1 – остовный, подграф G2 – порожденный.

163

(v i, vi 1 ) i 1,

a

b

c

a

b

c

a

c

a

b

c

d	e	f	d
	G

e	f	d
G1

e	f	d	e
G2			G3

Рисунок 18.4 – Подграфы

Изоморфные графы. Граф G называется изоморфным графу H (рис. 18.5), если существует биекция f из множества вершин графа G в множество вершин графа H , обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f ( A) в вершину f (B) и наоборот – если в графе H есть ребро из вершины A в

вершину B, то в графе G должно быть ребро из вершины f 1 ( A) в вершину f 1 (B) . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.

a	б	в
	Рисунок 18.5 – Изоморфные графы

Определение. Путѐм (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Определение. Ориентированным путѐм в орграфе называют конечную последовательность вершин v i i 1, ,k , для которой все пары

k 1 являются (ориентированными) рѐбрами.

164

Определение. Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рѐбер.

Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Определение. Путь (или цикл) называют простым, если ребра в нѐм не повторяются; элементарным (или контуром), если он простой, и вершины в нѐм не повторяются.

Несложно видеть, что:

всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины;

всякий простой неэлементарный путь содержит элементарный цикл;

всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-) цикл, проходящий через ту же вершину (или ребро);

петля – элементарный цикл.

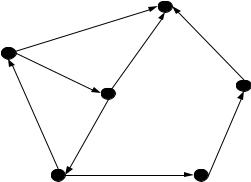
Пример. Рассмотрим граф на рис. 18.6. Он содержит пути: (5, 1, 2), (5, 6, 3, 2), (4, 5, 1, 4, 2) и т.д. Все эти пути простые, элементарным же является только последний. Цикл в графе только один – (1, 4, 5).

		2
	a
1		b
		c
d
		3
	4
e	f
		g
5	h	6

Рисунок 18.6 – Пути на графе

Бинарное отношение «существует путь из u в следовательно, разбивает

на	множестве вершин графа, заданное как
v »,	является отношением эквивалентности, и,
это	множество на классы эквивалентности,

165

называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный.

Определение. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Определение. Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G .

Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов

Определение. Ребро графа называется мостом, если его удаление увеличивает число компонент.

Определение. Вершина, удаление которой приводит к увеличению компонент связности, называется точкой сочленения.

Определение. Множество вершин, удаление которых (всех вместе), приводит к увеличению компонент связности, называется разделяющим

множеством.

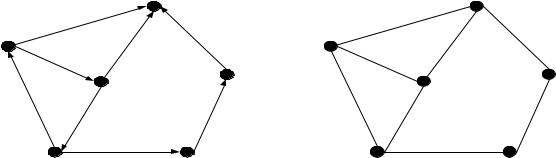
Пример. На рис. 18.7: в графе G1 – ребро (c, d ) – мост; в графе G2 – вершина c – точка сочленения; в графе G3 – множество вершин {c, g} – разделяющее множество.

a		e	b		d	b
							c	d
c	d			c
		a			e	a

		g	f	f	g	e
b	f
G1			G2		G3

Рисунок 18.7

Определение. Граф называется:

связным, если для любых вершин u, v есть путь из u в v.

сильно связным или ориентировано связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

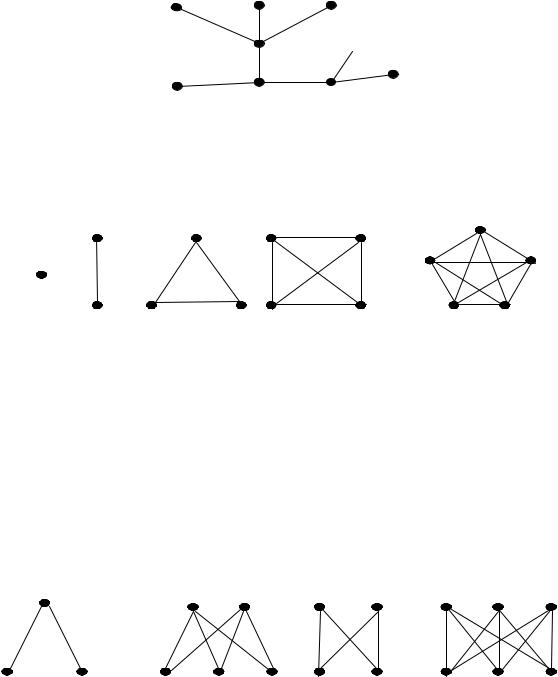
деревом, если он связный и не содержит простых циклов (рис 18.8).

166

1

2

3

	4
6	5

8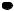

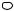9 7

Рисунок 18.8 – Граф – деревополным, если любые его две (различные, если не допускаются петли)

вершины соединены ребром. Полный граф с n вершинами обозначается Kn . На рис. 18.9 изображены полные графы K1, K2 , K3, K4 , K5 .

K1 K2 K3 K4 K5

Рисунок 18.9 – Полные графыдвудольным, если его вершины можно разбить на два

непересекающихся подмножества V1 и V2 так, что всякое ребро соединяет вершину из V1 с вершиной из V2 . Двудольный граф называется полным двудольным графом Kmn , если V1 содержит m вершин, V2 содержит n вершин

идля каждого a V1 , b V2 имеем (a,b) E . Таким образом, для каждого a V1

иb V2 имеется связывающее их ребро. На рис. 18.10 изображены полные двудольные графы K12 , K23 , K22 , K33 .

K12 K23 K22 K33

Рисунок 18.10 – Полные двудольные графы

k-дольным, если его вершины можно разбить на k непересекающихся подмножества V1,V2 ,...,Vk так, что не будет рѐбер, соединяющих вершины одного и того же подмножества.

планарным, если граф можно изобразить диаграммой на плоскости без пересечений рѐбер (рис. 18.11).

167

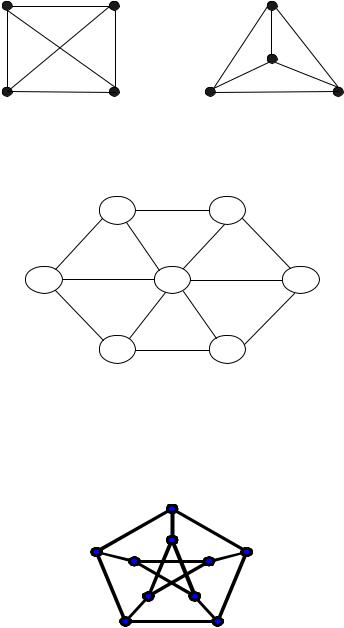
Рисунок 18.11 – Планарный граф K44 и его плоское изображение

взвешенным или нагруженным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра (рис. 18.12).

		20
	1		2
23		1		15
			4
6	36	7	9	3
		25	16
28
				3
		17
	5		4

Рисунок 18.12 – Нагруженный граф

однородным (регулярным) графом степени r , если степени всех вершин которого одинаковы и равны r . Граф третьей степени называют кубическим; этот граф обладает рядом интересных свойств и, в частности, он всегда имеет четное число вершин (рис. 18.13).

Рисунок 18.13 – Граф Петерсена – регулярный граф 3-й степени

18.4 Способы задания графов

18.4.1 Геометрическая реализация графа

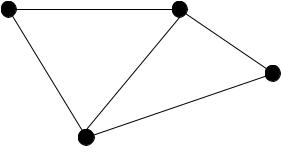
Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией (рис. 18.14).

168

1	a	2

b

	e	d
		3

c

4

Рисунок 18.14 – Геометрический способ задания графа При переходе от алгебраического способа к геометрическому одному и

тому же графу могут соответствовать различные изображения – изоморфные графы, при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф. Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично (с ним трудно работать, особенно ЭВМ), во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации.

18.4.2 Матрица инциденций (инцидентности)

При задании графа таблицей составляется таблица, состоящей из n строк (вершины) и m столбцов (ребра). На пересечении строк и столбцов пишутся соответствующие знаки, которые показывают отношение (инцидентность) вершины и ребра. Это может быть знаки ―+‖ и ― – ‖, числа 0,1, – 1 и др.

Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами n вершин V к m ребер X . Пусть дан граф G(V , X ) , где V {V1,V2 ,...,Vn} – вершины, а X {X1, X2 ,..., Xm} – ребра, среди которых могут и кратные ребра (есть вершины, которые соединяет несколько ребер).

Определение. Матрицей инциденций В данного графа будет таблица, состоящая из n строк (вершины) и m столбцов (ребра). При рассмотрении неориентированного графа на пересечении строк и столбцов ставится число 1, если соответствующие вершина и ребро инцидентны ( adj ) и ставится число 0,

169

если они не инцидентны. Элементы матрицы инциденций неориентированного графа определяются следующим образом:

		i	j
	1,	если v adj x		;
bij
	0,	в противном случае.

При рассмотрении ориентированного графа на пересечении строк и столбцов ставится число 1, если из вершины выходит соответствующее ее ребро. Если в вершину входит ребро, то ставят число (– 1). Если вершина не инцидентна ребру, то ставится число 0. Элементы матрицы инциденций неориентированного графа определяются следующим образом:

	1,	если vi	начало дуги x j ;
			конец дуги x j ;
bij	1,	если vi
	0,	если vi	не инцидентна ребру x j .

Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки – степень соответствующей вершины.

Матрицы инцидентности прямоугольные, если число строк и столбцов различно. Если число вершин и ребер в графе одинаковое, то получается квадратная матрица.

Пример. Построим матрицы инциденций для графов на рис. 18.15.

		2			2
	a			a
1		b	1		b
		c			c
d			d
		3			3
	4			4
e	f		e	f
		g			g
5	h	6	5	h	6

Рисунок 18.15 – Ориентированный и соответствующий ему неориентированный графы

170