ДМ_Конспект

Поиск всех гамильтоновых циклов производится так (вершина a берется в качестве отправной вершины):

№	Множество S	Комментарии
1	a	Добавляем первую возможную вершину в
		столбце a (вершину b ).
2	a,b	Добавляем первую возможную вершину в
		столбце b (вершину c ).
3	a,b,c	Первая возможная вершина в столбце c не
		является возможной ( a S ), добавляем

следующую вершину в столбце (вершину d ).

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

a,b,c, d

a,b,c,d, f

a,b,c, d

a,b,c

a,b a,b,e a,b,e,c a,b,e,c,d

a,b,e,c,d, f

a,b,e,c,d a,b,e,c a,b,e a,b,e,d

a,b,e,d, f

a,b,e,d, f ,c

Добавляем вершину f .

В столбце f нет возможных вершин. Возвращение.

В столбце d нет возможных вершин. Возвращение.

В столбце c нет возможных вершин. Возвращение.

Добавляем вершину e . Добавляем вершину c . Добавляем вершину d . Добавляем вершину f .

Гамильтонова цепь. Дуга ( f , a) дает гамильтонов цикл. Возвращение.

Возвращение. Возвращение.

Добавляем вершину d . Добавляем вершину f .

Добавляем вершину c .

Гамильтонова цепь. Дуга (c, a) дает гамильтонов цикл. Возвращение.

19	a,b,e,d, f	Возвращение.
20	a,b,e,d	Возвращение.
		201

21	a,b,e	Возвращение.
22	a,b	Возвращение.
23	a	Возвращение.
24		Конец поиска.

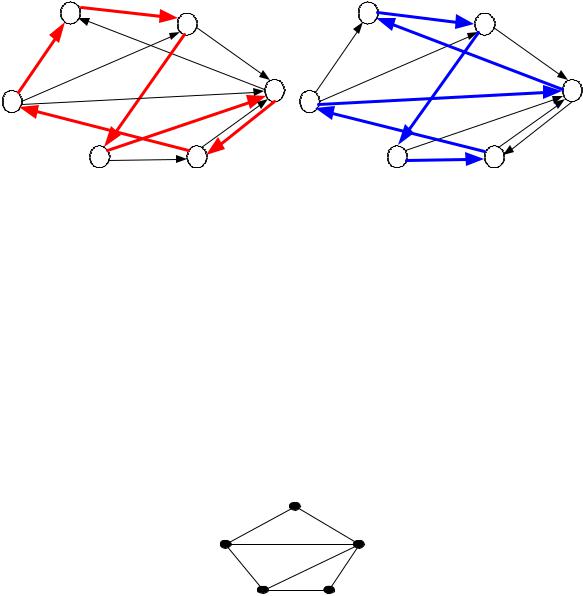
В результате получаем два гамильтоновых цикла (рис. 20.19).

a	b	a	b
f	c	f	c
e	d	e	d

Рисунок 20.19– Гамильтоновы циклы в графе

Определение. Реберным графом L(G) графа G называется граф, имеющий столько же вершин, сколько ребер у графа G . Ребро между двумя вершинами графа L(G) существует тогда и только тогда, когда ребра графа G , соответствующие этим двум вершинам, смежные (т. е. инцидентные одной и той же вершине графа G ).

Пример. На рис. 20.20 изображен исходный граф, а на рис. 20.21 – соответствующий ему реберный.

1 2

7

	5	6
		3

4

Рисунок 20.20

202

1

7

6

5

2

3

4

Рисунок 20.21 Гамильтонов граф является двусвязным, так как между каждой парой

вершин существует не менее чем две различные простые цепи.

20.10 Признаки существования гамильтоновых циклов, путей и контуров

Общий признак, при помощи которого для любого графа можно было бы определить, имеет он гамильтонов цикл или нет, не найден до сих пор. Существуют некоторые достаточные условия гамильтоновости графа (все графы предполагаются связными и простыми).

Если в графе есть висячая вершина (со степенью, равной единице), то гамильтонов цикл в нем отсутствует (рис. 20.22).

2

3

4

1

5

Рисунок 20.22

Теорема (условие Дирака). Если число n вершин графа G не менее трех

и степень

i deg xi любой

вершины

xi

не менее

n

( i

n

) , то граф

G

2

2

является гамильтоновым.

Теорема (условие Оре). Если в графе G с n

вершинами ( n 3) сумма

степеней

любых двух

вершин u

и

v

является

не

меньшей,

чем

n

( degu deg v n ), то граф G является гамильтоновым.

Теорема Бонди-Хватала. Пусть для упорядоченной по возрастанию

последовательности степеней

вершин

i deg xi ,

1 2 ... n,

графа

G

выполнены импликации

(

k) (

n k) ,

k :1 k

n

, тогда G

–

k

n k

2

гамильтонов граф.

203

Теорема (условие Харари). Реберный граф L(G) гамильтонов тогда и только тогда, когда в G существует цикл, содержащий хотя бы по одной вершине из каждого ребра графа G .

Следствие. Если граф G либо эйлеров, либо гамильтонов, то реберный граф L(G) гамильтонов.

Теорема (признак Кенига). В полном орграфе G (любая пара вершин которого соединяется хотя бы в одном направлении) всегда существует гамильтонов путь.

20. 11 Контрольные вопросы и задания

1.Дайте определение связного и несвязного графов.

2.Что называется степенью связности графа?

3.Перечислите свойства связных графов.

4.Приведите примеры метрических характеристик связных графов.

5.Дайте определения эйлерова цикла (эйлеровой линии, замкнутой эйлеровой цепи, эйлеровой цепи).

6.Какой граф называется эйлеровым?

7.Для решения каких практических задач используется теорема Эйлера?

8.Дайте определение гамильтонова пути (гамильтоновой цепи), гамильтонова цикла.

9.Какой граф называется гамильтоновым?

10.Охарактеризуйте применение задачи коммивояжера.

11.Приведите алгоритм Робертса-Флореса. Для каких целей он используется?

12Назовите основные признаки существования гамильтоновых циклов, путей и контуров.

13. Охарактеризуйте теорему (условие Дирака) для определения гамильтонова графа.

ЛЕКЦИЯ 21 ДЕРЕВЬЯ

21.1 Определение и свойства деревьев

Определение. Связный граф, не содержащий циклов, называется деревом

(рис. 21.1).

204

1

2

3

	4
6	5

8

9 7

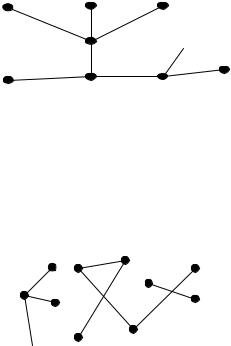
Рисунок 21.1 – Дерево Несвязный граф, не содержащий циклов, называется лесом.

Пример. На рис. 21.2 приведен трехкомпонентный лес. Первую компоненту образует дерево с вершинами 1,2,3,4, вторую – 5,6,7,8,9, третью –

10,11.

	1	7	6
			9

	10
2
3	11

8

5 4

Рисунок 21.2 – Лес

21.2 Свойства деревьев

Теорема 21.1. Всякое дерево содержит n 1 ребер, где n – число вершин. Теорема 21.2. Всякий лес содержит n k ребер, где k – число компонент

связности.

Теорема 21.3. Любые две вершины дерева соединены точно одной простой цепью.

Теорема 21.4. Если в дереве любые две вершины соединить ребром, то в графе появится один цикл.

21.3 Перечисление графов

Определение. Граф G ( X ,Y ) называется помеченным, если его вершинам присвоены фиксированные метки, например, номера 1,2,..., n .

Два помеченных графа одинаковы (не различаются), если их вершины помечены одной системой меток и существует изоморфизм одного графа на другой, при котором сохраняются метки всех вершин.

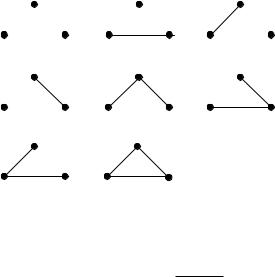
Пример. На рис. 21.3 изображены все помеченные графы с числом вершин n 3 ; их количество равно 8.

205

1	1		2	1	3	1
2		3	2	3	2	3
4	1		5	1	6	1
2		3	2	3	2	3
7	1		8	1
2		3	2	3
			Рисунок 21.3
Количество Gnm	(неориентированных)					помеченных (n, m) графов

(простых с n вершинами и m ребрами) равно числу сочетаний из множества различных неориентированных пар вершин {(xi, xj)} по числу ребер m .

				Gnm CСm n2 CmS , S Сn2				n(n 1)
							2
Суммируя				числа Gnm	по	всем	возможным			количествам ребер
m 1,2,...,	n(n 1)			от случая безреберного графа до случая полного графа с n
		2
вершинами, получаем число Gn					всех помеченных графов с n вершинами:
						S
					Gn CmS		2S
						m 0
Число		gn		неизоморфных		графов без				пометок (простых,

неориентированных) найти значительно труднее. Среди восьми графов на рисунке 3 без учета пометок можно указать только четыре попарно неизоморфных друг другу, например, в квадратах 1, 2, 7, 8. Следовательно, g 3 4 , что вдвое меньше числа G3 помеченных графов. Число G4 помеченных

четырехвершинных графов равно 64, в то время как различных неизоморфных четырехвершинных графов без пометок существует всего g4 11.

Если через	gnm	обозначить число неизоморфных n -вершинных графов с m
		S
ребрами, то	g n	g nm
		m 0

В общем случае количество неизоморфных графов gnm , gn находятся с помощью теории перечисления конфигураций, созданной Д. Пойа.

206

21.4 Перечисление деревьев

Введем обозначения: n – число помеченных деревьев с n вершинами. tn – число обычных (неизоморфных) деревьев с n вершинами.

Пример. На рис. 21.4 изображены все помеченные четырехвершинные деревья. Их 16.

1	1		2	1		3	1		4	1
2		3	2		3	2		3	2	3
	4			4			4			4
5	1		6	1		7	1		8	1
2		3	2		3	2		3	2	3
	4			4			4			4
9	1		10	1		11	1		12	1
2		3	2		3	2		3	2	3
	4			4			4			4
13	1		14	1		15	1		16	1
2		3	2		3	2		3	2	3
	4			4			4			4

Рисунок 21.4

Формула А. Кэли. Число n помеченных деревьев с n вершинами равно nn 2 , т.е. n nn 2 .

Числа tn обычных (неизоморфных) деревьев являются значительно меньшими, однако вычислить их существенно труднее. Современные алгоритмы нахождения значений tn и получения конфигураций неизоморфных деревьев с n вершинами основаны на теории перечисления Д. Пойа.

Важный класс графов образуют деревья с одной помеченной вершиной, которая называется корнем. Само дерево с одной помеченной («выделенной») вершиной называется корневым деревом. Число корневых деревьев с n вершинами обозначается через Tn (tn Tn n ) .

Все корневые деревья с числом вершин n 3 изображены на рисунке

21.5.

207

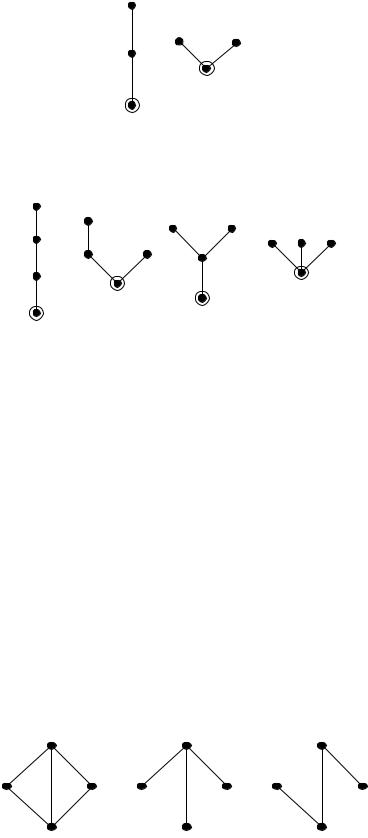
Рисунок 21.5

Все корневые деревья с числом вершин n 4 изображены на рис. 21.6.

Рисунок 21.6

21.5 Остовы графа

Если связный граф содержит цикл, то после удаления любого ребра, входящего в цикл, этот цикл разрушается, но связность графа сохраняется. Применим операцию разрушения циклов к каждому циклу графа. Тогда в графе не останется циклов и получится связный частичный граф, являющийся деревом.

Определение. Полученное дерево называется остовом, т. е. остовом называется связный частичный граф данного связного графа G , содержащий все вершины графа G , но не содержащий циклов.

Пример. Рассмотрим, например, граф, изображенный на рис. 21.7. Удалим из него ребра {1,4} и {3,4} и получим остов. Если удалить ребра {1,2} и {3,4} , то получим другой остов.

2		2			2
1	3	1	3	1	3

4

4

4

Рисунок 21.7

Два остова в G считаются различными, если они отличаются хотя бы одним ребром.

208

nn 2

Для того чтобы G имел более одного остова, необходимо и достаточно существование хотя бы одного цикла в G .

Для полного (простого) графа G перечисление остовов есть перечисление всех помеченных деревьев с вершинами графа G , так что число остовов равно .

В общем случае число остовов получил Кирхгоф.

Определение. Матрицей Кирхгофа K (G) простого графа G называется n n -матрица с элементами, которые определяются так:

		1, если вершины xi,xj смежны;
k i , j	0, если вершины xi,xj не смежны;
		i deg xi, если i j.

Сумма элементов в каждой строке и каждом столбце матрицы K (G) равна нулю.

Теорема Кирхгофа. Число остовных деревьев в простом связном графе G с n вершинами равно алгебраическому дополнению любого элемента матрицы Кирхгофа K (G) .

21.6 Алгоритмы построения остовов графа

Задача отыскания кратчайшего остова графа является классической задачей теории графов. Методы решения этой задачи послужили основой для многих других важных результатов. Задача о нахождении кратчайшего остова принадлежит к числу немногих задач теории графов, которые можно считать полностью решенными. Между тем, если изменить условия задачи, на первый взгляд даже незначительно, то она оказывается значительно более трудной.

Алгоритм строит остов:

Вход: граф G(V , E) , заданный матрицей длин рѐбер C .

Выход: остов GT (V ,T ) .

T : V ;

while в T больше одного элемента do взять любое поддерево из T найти к нему ближайшее соединить эти деревья в T

end while

209

Вчастности, исследования алгоритма Краскала привели в конечном счете

ктеории жадных алгоритмов. Следующий жадный алгоритм, известный как алгоритм Краскала, находит кратчайший остов в связном графе.

Алгоритм Краскала

Вход: список E рѐбер графа G с длинами. E p .

Выход: множество T рѐбер кратчайшего остова.

T :

Упорядочить E в порядке возрастания длин k : 1 { номер рассматриваемого ребра }

for k from 1 to p 1 do

while добавление ребра E(k) образует цикл в T do k : k 1 {пропустить ребро }

end while

T : T {E[k]} {добавить это ребро в SST } end for

(SST-Shortest Sceleton Tree - стандартное обозначение для кратчайшего остова).

Пример. Дан нагруженный граф G . Необходимо построить минимальное остовное дерево GT .

Алгоритм: Строим таблицу, в которую заносим все ребра с их стоимостями в порядке возрастания. На каждом шаге алгоритма включаем в остовное дерево ребро графа минимальной стоимости, проверяя, не образуется ли цикл с уже включенными в дерево ребрами.

		20
	1		2
23		1		15
			4
6	36	7	9	3
		25	16
28
				3
		17
	5		4

Рисунок 21.8

210