ДМ_Конспект

Таблица 18.1 – Матрица инциденций ориентированного графа (рис. 18.15а)

		a	b	c		d		e	f	g		h
1		1	0	0		1		-1	0	0		0
2		-1	-1	-1		0		0	0	0		0
3		0	1	0		0		0	0	-1		0
4		0	0	1		-1		0	1	0		0
5		0	0	0		0		1	-1	0		1
6		0	0	0		0		0	0	1		-1
Таблица		18.2	– Матрица		инциденций			неориентированного			графа (рис.
18.15б)
		a	b	c		d		e	f	g		h
1		1	0	0		1		1	0	0		0
2		1	1	1		0		0	0	0		0
3		0	1	0		0		0	0	1		0
4		0	0	1		1		0	1	0		0
5		0	0	0		0		1	1	0		1
6		0	0	0		0		0	0	1		1

Несложно заметить, что количество единиц в строке, соответствующей вершине, для ориентированных графов определяет полустепень исхода, количество (-1) – полустепень захода. Для неориентированных графов – просто степень вершины.

18.4.3 Матрица смежности

Матрицу можно сделать квадратной для любого графа. В таких случаях строки и столбцы изображают вершины. На пересечении строк и столбцов ставится число, если соответствующие вершины соединены ребром (ребрами) и ставится число 0, если вершины не соединены.

Определение. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n ) – это квадратная матрица A размера n , в которой значение элемента cij равно числу ребѐр из i –й вершины

графа в j –ю вершину.

Матрица смежности неориентированного графа является симметричной и не меняется при транспонировании. Хотя формально каждая вершина всегда смежная сама с собой, в матрице смежности мы будем ставить 0, если у нее нет

171

петли, и 1, если есть одна петля. Если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули. Элементы матрицы смежности определяются следующим образом:

a, если вершины xi и xj соединяет а ребер; cij 0, если вершины xi и xj не смежны.

Матрица смежности ориентированного графа не симметрична. Элементы ее определяются следующим образом:

	a,	если из вершины xi в xj ведет а ребер;
cij
	0,	в противном случае.

Пример. Построим матрицы смежности для графов на рисунке 18.15.

Таблица 18.3 – Матрица смежности ориентированного графа (рис. 18.15а)

	1	2	3	4	5	6
1	0	1	0	1	0	0
2	0	0	0	0	0	0
3	0	1	0	0	0	0
4	0	1	0	0	1	0
5	1	0	0	0	0	1
6	0	0	1	0	0	0

Сумма элементов по строке равна степени полуисхода вершины, сумма элементов по столбцу – степени полузахода вершины.

Таблица 18.4 – Матрица смежности неориентированного графа (рис. 18.15б)

	1	2	3	4	5	6
1	0	1	0	1	1	0
2	1	0	1	1	0	0
3	0	1	0	0	0	1
4	1	1	0	0	1	0
5	1	0	0	1	0	1
6	0	0	1	0	1	0

Сумма элементов по строке (и по столбцу) равна степени вершины.

172

18.4.4 Список ребер

Определение. Список рѐбер – это тип представления графа в памяти компьютерной программы, подразумевающий, что каждое ребро представляется двумя числами – номерами вершин этого ребра. Список рѐбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

Более абстрактно, граф можно задать как тройку V , E, , где V и E – некоторые множества (вершин и рѐбер, соответственно), а – функция

инцидентности, сопоставляющая каждому ребру e E (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов).

На основе рассмотренных понятий можно дать окончательные определения неориентированного и ориентированного графов.

Определение. Назовем абстрактным неориентированным графом

G( X , E,) совокупность непустого множества					X , произвольного множества
E , причем	X E , и		произвольного		отображения		: E X X .
Элементы множеств		X и E – соответственно вершины и ребра графа, а –
отображение инцидентности (отношение смежности).
Определение.		Абстрактный		ориентированный			граф		(орграф)
G( X , E,) представляет собой совокупность						непустого	множества X ,
произвольного множества E ,			причем такого, что			X E ,	и произвольного
отображения	: E X X ;		элементы множеств X и					E	являются
соответственно вершинами и дугами графа G , а							–	отображение
инцидентности (отношение смежности).
18.4.5 Число вершин и ребер графа
Теорема	18.1.	Сумма	степеней	вершин		неориентированного графа

G( X , E,) равна удвоенному числу его ребер, т.е. если m E , то (x) 2m .

x X

Это утверждение почти очевидно и следует из того, что каждое ребро графа инцидентно ровно двум вершинами, и поэтому вклад каждого ребра в сумму степеней вершин равен двум.

Теорема 18.2. В неориентированном графе G( X , E,) число вершин нечетной степени четно.

173

Для доказательства этого утверждения разобьем множество вершин	X
графа на два подмножества X 0 и X1 , X X0 X1 , причем X 0 и X1	–

соответственно множества вершин графа, имеющих четные и нечетные степени. С учетом теоремы 18.1 можно записать:

(x) (x) (x) 2 (x) .

x X1 x X x X0 x X0

В правой части этого выражения – разность двух целых четных чисел,

поэтому и (x) должна быть величиной четной. Но это может быть только в

x X1

том случае, если и X1 четно.

Для ориентированного графа сумма полустепеней исхода равна сумме полустепеней захода и равна количеству ребер графа:

(x) (x)		1	(x) m .
x X	x X	2 x X

18.5 Контрольные вопросы и задания

1.Дайте определения графа.

2.Какой граф называется неориентированным? Приведите примеры.

3.Какой граф называется ориентированным? Приведите примеры.

4.Какой граф называется пустым?

5.Дайте определение полного графа. Приведите примеры.

6.Какие вершины являются смежными в графе?

7.Какие вершины и ребра инцидентны в графе. Приведите примеры.

8.Дайте определение абстрактного ориентированного графа.

9.Перечислите способы задания графов.

10.Как составляется матрица смежности? Приведите пример.

11.Что такое матрица инциденций? Приведите пример.

12.Поясните геометрический способ задания графа.

13.Чему для ориентированного графа равна сумма полустепеней исхода?

14.Какой граф называется взвешенным или нагруженным?

15.Дайте определение пути в графе.

16.Дайте определения цикла в графе.

17.Поясните понятие маршрута в графе.

18.Приведите пример изоморфных графов.

174

19.Какой граф называется связным?

20.Дайте определение компоненты связности.

21.Как определить степень вершины графа?

22.Какой граф называется деревом?

ЛЕКЦИЯ 19. ОПЕРАЦИИ НАД ГРАФАМИ. ИЗОМОРФИЗМ ГРАФОВ.

ПЛОСКИЕ И ПЛАНАРНЫЕ ГРАФЫ

19.1 Операции над графами

19.1.1 Операции удаления ребер и вершин

Удаление ребра. Пусть u,v – ребро графа G (V , E) . Граф

G u ,v G u,v получается из графа G в результате удаления ребра u,v , т.е.

V G u ,v V G , E G u ,v E G \ u,v .

1

1

		u				u	v
			v
		4	5	2	3	4	5
2	3
		6				6
		Рисунок 19.1 –Удаление ребра
Удаление вершины. Пусть			v	– вершина	графа G . Граф		G p G v

получается из графа G в результате удаления вершины v и всех инцидентных ей ребер, т.е. V G p V G \ {v}, E G p E G \ v,u u V G .

u

G

G(u)

Рисунок 19.2 –Удаление вершины u .

175

19.1.2 Операция введения вершины в ребро и операция введения ребра в

граф

Операция введения вершины в ребро. Пусть G V , E и e (u,v) E.

Операция введения вершины w в ребро e (u,v)					преобразует это ребро в два
ребра e1 (u, w) и e2 (w,v) .
u	e	v	u	e1	w	e2	v

Рисунок 19.3 – Введение вершины

Операция введения ребра в связный граф G V , E состоит в том, что в граф G вводится ребро между двумя несмежными вершинами u и v . Эта операция выражается через операцию объединения графа G и дерева Tuv Формально это записывается так: wik G,u,v G Tu ,v G Tv,u wik G,v,u .

Корректность такого представления следует из того, что объединение двух связных графов, имеющих общие вершины, будет связным графом. Ясно также, что справедливо тождество вида

wok wik G,u,v ,u,v wik wok G,u,v ,u,v G .

u u

G	w	w

Рисунок 19.4 – Введение ребра

19.1.3 Дополнение графа

Определение. Дополнением графа G (V , X1 ) с n вершинами называется граф G (V , X 2 ) , который содержит все вершины графа G и те ребра, которые принадлежат полному графу Kn (V , X ) , но не принадлежат графу G , т.е. X X1 X2 , X1 X2 .

176

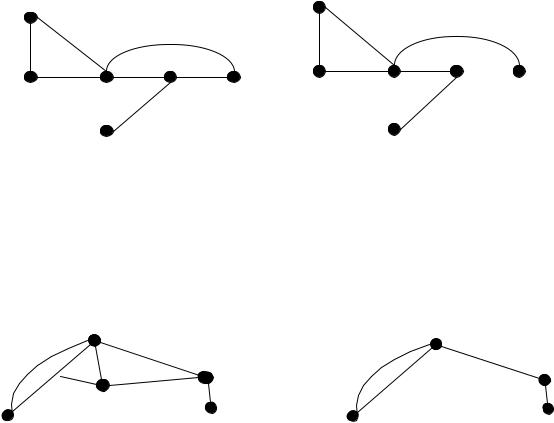
Пример. На рис. 19.5 изображен граф и его дополнение.

Рисунок 19.5 – Граф и его дополнение

19.1.4 Объединение графов

Определение. Объединением графов G1 V1, E1 и G2 V2 , E2 называют

граф такой, что V V1 V2 , G V , E G1 G2 , E E1 E2.

Объединение графов G1 и G2 называется дизъюнктным, если

V1 V2 .

Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

1.G1 G2 G2 G1 – свойство коммутативности;

2.G1 (G2 G3 ) (G1 G2 ) G3 – свойство ассоциативности.

Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.

Теорема 19.1. Пусть G1 и G2 – два графа (ориентированные или не

ориентированные одновременно)		с одним и тем же множеством вершин X , и
пусть C1 и C2 – матрицы смежности вершин этих графов. Тогда матрицей
смежности вершин графа G1 G2		является матрица C C1			C2 , образованная
поэлементным логическим сложением матриц C1				и C2 .
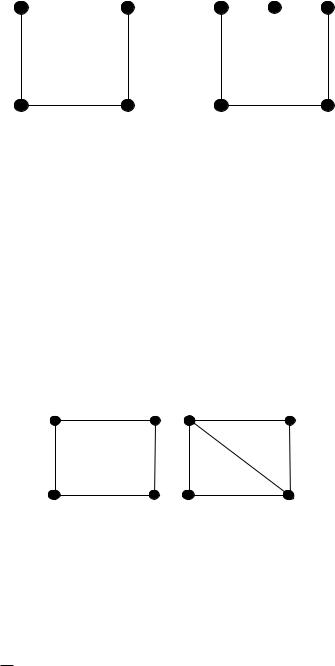
		1	2	1	2	5
				5
1
	2
	3	4	3
				4		3
4			G2	G2UG1
	G1

Рисунок 19.6 – Объединение графов

177

1	4	1	4

		2	=			2
3	G1	5		3		5
		G2			G1UG2

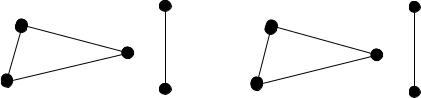
Рисунок 19.7 – Дизъюнктное объединение графов

19.1.5 Пересечение графов
Определение. Пусть G1 V1, E1		и G2 V2 , E2 – произвольные графы.
Пересечением G1 G2 графов G1	и G2	называется граф с множеством вершин
X1 X2 с множеством ребер (дуг)	E E1 E2 .

Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

1.G1 G2 G2 G1 – свойство коммутативности;

2.G1 (G2 G3 ) (G1 G2 ) G3 – свойство ассоциативности.

Для того чтобы операция пересечения была всеобъемлющей, необходимо

ввести понятие пустого графа.
Определение. Граф G( X , E) называется пустым, если множество	X
вершин графа является пустым ( X ). Заметим, что в этом случае	и

множество E ребер (дуг) графа также пустое множество ( E ). Пустой граф обозначается символом . Такой граф может быть получен в результате выполнения операции пересечения графов, у которых X1 X2 . В этом случае говорят о непересекающихся графах.

Теорема 19.2. G1 и G2 – два графа (ориентированные или неориентированные одновременно) с одним и тем же множеством вершин X , и пусть C1 и C2 – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа G1 G2 является матрица C C1 C2 , образованная поэлементным логическим умножением матриц C1 и C2 .

178

1	2	1	2	5
		5

1

	2
	3	4	3
				3
4			G2	G2∩G1
	G1

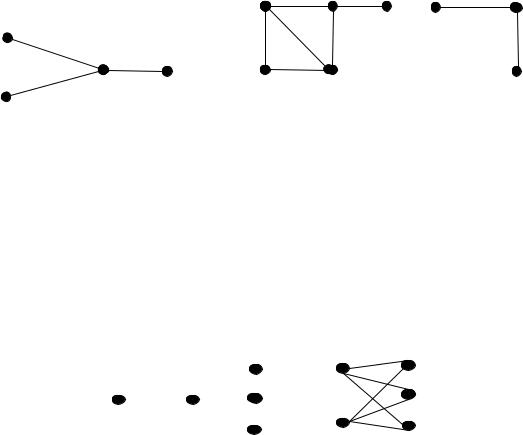
Рисунок 19.8 – Пересечение графов

19.1.6 Соединение графов

Определение. Соединением (сильным произведением) графов G1 V1, E1

и

G2 V2 , E2

(V1 V2 )

называют

граф

такой,

что

G V , E (V V1 V2 , E (E1 E2 ) (V1 V2 )).

u

1

u

1

2

+

v

=

v

G1

w

2

w

G1+G2

G2

Рисунок 19.9 – Соединение графов

19.1.7 Композиция графов

Определение. Пусть G1 ( X , E1 ) и G2 ( X , E2 ) – два графа с одним и тем же

множеством вершин X . Композицией G1 (G2 ) графов G1	и G2	называется граф
с множеством вершин E , в котором существует дуга	(xi , xj )	тогда и только

тогда, когда существует дуга (xi , xk ) , принадлежащая множеству E1 , и дуга (xk , xj ) , принадлежащая множеству E2 .

Пример. Рассмотрим выполнение операции композиции G1 (G2 ) на графах, изображенных на рис. 6.25.

179

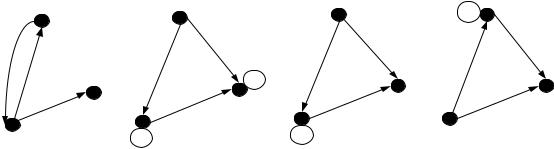
	X2	X2	X2	X2
		X3
		X3	X3	X3
		X1	X1
X1				X1
G1		G2	G1(G2)	G2(G1)

Рисунок 19.10 – Композиция графов

Для рассмотрения операции составим таблицу 19.1, в первом столбце которой указываются ребра (xi , xk ) , принадлежащие графу G1 , во втором — ребра (xk , xj ) , принадлежащие графу G2 , а в третьем — результирующее ребро (xi , xj ) для графа G1 (G2 ) .

Таблица 19.1 – Построение композиции графов G1 (G2 )

G1	G2	G1 (G2 )
(x1, x2 )	(x2 , x1 )	(x1, x1 )
	(x2 , x3 )	(x1, x3 )
(x1, x3 )	(x3 , x3 )	(x1, x3 )
(x2 , x1 )	(x1, x1 )	(x2 , x1 )
	(x1, x3 )	(x2 , x3 )

Заметим, что дуга (x1, x3 ) результирующего графа в таблице встречается дважды. Однако, поскольку рассматриваются графы без параллельных ребер (дуг), то в множестве E результирующего графа дуга (x1, x3 ) учитывается

только один раз, т.е. E {(x1, x1 ), (x1, x3 ), (x2 , x1 ),(x2 , x3 )}.

На рис. 19.10 изображены графы G1 и G2 и их композиция G1 (G2 ) . На этом же рисунке изображен граф G2 (G1 ) . Рекомендуется самостоятельно построить граф G2 (G1 ) , и убедиться, что графы G1 (G2 ) и G2 (G1 ) не изоморфны.

19.1.8 Произведение графов

Определение. Декартовым произведением G1 G2 называется граф G ,

для которого V (G) V1 V2 – декартово произведение множеств вершин исходных графов, а E(G) определяется следующим образом: вершины (u1,u2 ) и

180