ДМ_Конспект

2	0	1	1
3	0	2	3	1
4	0	6	11	6	1
5	0	24	50	35	10	1
6	0	120	274	225	85	15	1
7	0	720	1764	1624	735	175	21	1
8	0	5040	13068	13132	6769	1960	322	28	1
9	0	40320	109584	118124	67284	22449	4536	546	36	1

Треугольник Стирлинга для числа циклов

Теорема. Имеет место соотношение

Доказательство.	n	обозначает
	k

n	n
	k	n!
k 0

число перестановок n объектов,

которое содержит ровно k циклов. Если просуммировать по всем k , то должно получиться общее число перестановок, равное n!.

Число Стирлинга второго рода S(n,k) равно количеству способов разбиения множества из n элементов на k непустых подмножеств и

обозначается nk (читается ― k подмножеств из n ‖).

Пример. Например, существует 7 способов разбиения четырехэлементного множества на две части:

1, 2,3 4 , 1, 2, 4 3 , 1,3, 4 2 ,2,3, 4 1 , 1, 2 3, 4 , 1,3 2, 4 , 1, 4 2,3

Поэтому 42 7 .

Рассмотрим значения чисел Стирлинга для малых значений k :

1. k 0. Существует только один способ разбиения пустого множества на нулевое число непустых частей, поэтому 00 1. Для непустого множества

нужна по крайней мере хотя бы одна часть, так что 0n 0 при n 0 .

2. k 1. Существует только один способ помещения n элементов в одно-

единственное непустое множество, поэтому 1n 1 при n 0 . Однако 10 0 ,

так как 0-элементное множество пусто.

151

3. k 2 . Очевидно, что	0 0 . Если множество из	n 0 объектов
	2

разделено на две непустые части, то одна из этих частей содержит последний объект и некоторое подмножество из n 1 объектов. Имеется 2n 1 подмножеств

из	n 1 объектов. Поскольку все объекты нельзя поместить в одну часть, то
n 2n 1 1.
2

n	0n	1n	n2	3n	n4	5n	6n	7n	8n	9n
0	1
1	0	1
2	0	1	1
3	0	1	3	1
4	0	1	7	6	1
5	0	1	15	25	10	1
6	0	1	31	90	65	15	1
7	0	1	63	301	350	140	21	1
8	0	1	127	966	1701	1050	266	28	1
9	0	1	255	3025	7770	6951	2646	462	36	1

Треугольник Стирлинга для числа подмножеств.

Выведем рекуррентное соотношение, при помощи которого можно будет вычислить значения nk . Если задано множество из n 0 объектов, которое должно быть разбито на k непустых частей, то мы либо помещаем последний

объект в отдельный класс, а оставшиеся n 1 объект разбиваем на			k 1 часть
n 1 способами, либо помещаем его в любую из	k частей,	на которые
k 1
разбиты n 1 объект. В последнем случае имеется	k n 1		возможных
	k

вариантов, поскольку каждый из kn 1				способов распределения первых n 1
объектов по k		непустым частям дает		k подмножеств, с которыми можно
объединить n ый объект. Имеем рекуррентную формулу:
n	n 1	n 1
k k 1 k k			, n 0

152

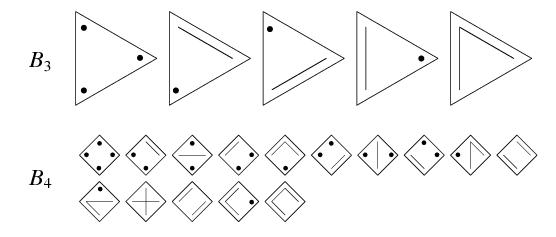
16.6.3 Числа Белла

Число Белла Bn равно количеству разбиений множества из n элементов на произвольное количество непустых подмножеств, которые не пересекаются. Очевидно, что B0 1, так как существует только одно разбиение пустого множества. Например, B3 5, так как существует 5 возможных разбиений множества a,b,c из трех элементов:

a , b , c , a,b c , a,c , b , a , b,c , a,b,c .

	Заметим, что n элементов можно разбить на i множеств (1 i n) . При
этом количество разбиений							n – элементного множества на k									подмножеств
равно		числу		Стирлинга			2 рода			S(n,k) .		Откуда		получаем			формулу
	n
Bn S (n, k) .
k 1
n	0		1		2	3		4		5	6		7	8		9		10
Bn	1		1		2	5		15		52	203		877	4140		21147		115975

Рассмотрим следующие конструкции, в которых точки обозначают одноэлементные множества, а сегменты объединяют элементы, принадлежащие одному множеству. Из n элементов можно построить Bn разных таких конструкций.

Теорема. Числа	Белла удовлетворяют следующему рекуррентному
n
соотношению Bn 1 Cnk Bk
k 0
Доказательство.	Рассмотрим разбиение (n 1) элемента в зависимости

от величины блока, в котором находится (n 1) – ый элемнент. Пусть размер

153

этого блока равен j

(1 j n n 1) . Тогда существует C j 1 способов выбрать

n

в него кроме (n 1) – ого еше ( j 1)

элемент. Остальные (n 1 j) элементов

можно разбить Bn 1 j

способами.Таким образом:

n 1

n 1

n

Bn 1 Cnj 1Bn 1 j Cnn 1 j Bn 1 j Cnk Bk

j 1

j 1

k 0

Пример.Например,

B C0B C1B C3B 1*1 3*1 3* 2 1*5 15 .

4

3

0

3

2

3

3

Числа Белла удовлетворяют следующему свойству:

B0

B1

B2

...

Bn

n

B1

B2

B3

...

Bn 1

i!

...

...

...

...

...

i 1

Bn

Bn 1

Bn 2

...

B2n

Для значений n 0,1,2,... получим следующие значения детерминанта:

1,

1,

2,

12,

288,

34560,

24883200,

125411328000,

5056584744960000,

1834933472251084800000, 6658606584104736522240000000, …

При

разложении функции

eex

в

ряд Маклорена

коэффициенты ряда

x

1x

2x

2

5x

3

образуют числа Белла: ee

e 1

...

1!

2!

3!

Числа Bn

могут быть

построены

при

помощи треугольника Белла.

Первая строка содержит 1. Каждая следующая строка начинается числом, стоящим в конце предыдущей строки. Каждое следующее число в строке равно сумме чиел, стоящих слева и сверху от него. Числа Белла образуют последние числа в строках.

154

16.7 Композиции

16.7.1 Понятие композиции чисел

При решении задач про распределение n одинаковых предметов между k непустыми урнами можно говорить о разложении числа n в сумму натуральных слагаемых ni : n n1 n2 ... nk , где k 1, ni 1

Два таких разложения числа n считаются разными, если они отличаются хотя бы одним слагаемым. В таком случае говорят о композиции числа n . В ином случае, композиция числа n – это его разложение в виде n n1 n2 ... nk , где учитываются как величины слагаемых (частей) ni , так и порядок их расположения в сумме.

Пример. Выписать все композиции числа 3.

Композиции имеют вид3=3, 3=2+1, 3=1+2, 3=1+1+1.

16.7.2 Композиции с ограничениями на количество слагаемых

Число композиций (k, n) числа n из k слагаемых равно числу распределений n одинаковых предметов по k разным урнам при условии отсутствия пустых урн. Число предметов, которые попали в урну с номером i , дает слагаемое ni . Отсюда выплывает, что (k, n) Cnk 11 .

Число всех композиций числа n равно nk 1 (k,n) nk 1Cnk 11 2n 1 . 16.8 Комбинаторика разбиений

При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой

игры карты раскладываются на 3 кучки (по числу играющих)				и 2	карты
кладутся в ―прикуп―. Играют 32 картами, т.е. каждый игрок получает по 10					карт.
	Определим		количество вариантов расклада при игре в	преферанс:
32!
N		. Для	обоснования полученной формулы расставим	все	карты
	(10!)3 2!

подряд и переставим их 32! способами. При каждой перестановке будем выделять первые 10 карт первому игроку, вторую десятку – второму, третью – третьему, а последние 2 карты будем откладывать в ―прикуп‖. После этого

155

заметим, что перестановка 10 карт в руках каждого игрока не меняет варианта расклада, как и положения 2 карт в прикупе. Поэтому 32! разделим три раза на 10! и еще на 2!. В общем случае, если раскладываются n разных предметов по

k ящикам так, чтобы в 1-й ящик (кучку, игроку в руки) попало						предметов,
во второй n2 предмета, в k -й –	nk предметов,			при этом n1 n2		... nk n , то
число вариантов расклада P(n1, n2	,..., nk )		n!		.
		n1	!n2 !...nk !

16.9 Контрольные вопросы и задания

1.Какой предварительный анализ содержания задачи необходимо осуществить, чтобы можно было применить урновые схемы решения?

2.Какую формулу необходимо использовать, чтобы решить задачу о распределении n разных предметов по k урнам?

3.Какую формулу необходимо использовать, чтобы решить задачу о распределении n одинаковых предметов по k урнам?

4.Какую формулу необходимо использовать, чтобы решить задачу о распределении разных предметов без учета порядка предметов в урнах?

5.Какие формулы необходимо использовать, чтобы решить задачу о распределении разных предметов между одинаковыми урнами при условии, что урны не пустые?

6.В каких комбинаторных задачах используются числа Моргана, Стирлинга, Белла?

7.Какую формулу необходимо использовать, чтобы решить задачу о распределении разных предметов с учетом их порядка в урнах?

8.Охарактеризуйте понятие композиции чисел.

9.Дайте характеристику разбиений в комбинаторном анализе.

ЛЕКЦИЯ 17. ПОДХОДЫ К ИЗУЧЕНИЮ КОМБИНАТОРНЫХ ОБЪЕКТОВ И ЧИСЕЛ

17.1 Понятие продуктивной функции

Пусть задана некоторая последовательность чисел a0 ,a1,a2 ,...,an ,...

Определение. Если степенной ряд

156

	a	a x a x2		... a xn ...		(17.1)
	0	1	2		n
совпадает при некоторых	с	функцией			f (x) , то	f (x) называется

продуктивной функцией для последовательности a0 ,a1,a2 ,...,an ,....

С последовательностью a0 ,a1,a2 ,...,an ,... можно связать еще один степенной ряд:

	a	a x a		x2	... a	xn			(17.2)
	0	1	2	2!	n n!
Определение. Если этот ряд совпадает с функцией (x) , то									(x)
называется	экспоненциальной			продуктивной				функцией	для

последовательности a0 ,a1,a2 ,...,an ,... Это название объясняется тем, что для последовательности 1, a, a2 ,..., an ,... экспоненциальной продуктивной функцией

(17.2) есть экспонента eax :

eax 1 ax

a2 x2

...

an xn

...

(17.3)

2!

n!

Для той же последовательности обычная функция есть

1

:

1 ax

(1 ax) 1 1 ax a2 x2

... an xn ...

(17.4)

Действительно, если q ax,

q

1, то есть

x

1

,

тогда

по формуле

a

суммы бесконечно спадающей геометрической прогрессии (17.4) получаем

11 q q2 ... 1 ax a2 x2 ... .

1q

Вчастности, если a 1, то

				1	1			x x2 ... xn ...,					x				1					(17.5)
		1 x
Дифференцирование (17.5) приводит к равенству
1				1	2x 3x2				... nxn ...,			x				1						(17.6)
	(1 x)2
Умножение (17.6) на x дает
				1			x 2x2 3x3 ... nxn ...,												x		1	(17.7)
			(1 x)2

157

(0)...

Таким образом,	1	есть продуктивная функция для последовательности
	1 x
чисел натурального ряда 1,2,3,4... (17.6),			x	– продуктивная функция для
			(1 x)2

последовательности 0,1,2,3,... (17.7).

Функцию f (x) , у которой есть производные произвольно высокого порядка при t 0, можно считать экспоненциальной продуктивной функцией для последовательности своих производных f (0), f (0), f (0),..., f (n)

Действительно получается разложение в рад Тейлора:

f (x) f (0) f (0)x f (0) x2 ,..., f (n) (0) xn ... .

2! n!

17.2Рекуррентные соотношения в комбинаторике

17.2.1Задача о наклейке марок

Имеются марки достоинством в 4, 6, 10 копеек. На конверт нужно наклеить марки так, чтобы сумма составляла 18 копеек. Будем считать, что порядок наклеиваемых марок важен, т. е. способы наклейки марок достоинством в 4, 10, 4 копейки и 10, 4, 4 разные способы.

Тогда можно написать следующее	рекуррентное соотношение:
F(N) F(N 4) F(N 6) F(N 10) , где под	F (N ) понимается количество

вариантов наклейки марок общей стоимостью N .

Подсчитаем значения F (N ) для некоторых начальных N .

F(N ) 0 при N 0 . F (0)1. F(1) F(2) F(3) 0 . F(4) 1. F(5) 0 . F(6) 1. F(7) 0 . F(8) 1. F(9) 0 . F(10) 3.

Тогда для N 18 получаем:

F(18) F(14) F(12) F(8) F(10) F(8) F(4) F(8) F(6) F(2) F(8) 3 1 1111 8 .

17.2.2 Задача об уплате долга

В кошельке имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20, 50 копеек (по одной штуке). Требуется уплатить долг в 73 копейки.

Запишем рекуррентное соотношение в общем случае, когда монеты имеют достоинства в k1,k2 ,...,km копеек и требуется набрать сумму в N копеек:

158

F(k1,k2 ,...,km; N) F(k1,k2 ,...,km 1; N km ) F(k1,k2 ,...,km 1; N) .

Первый член правой части учитывает количество комбинаций, в которых монета старшего достоинства использована, второй член – в которых монета старшего достоинства не использована. Для рассматриваемого примера

F (1, 2, 3, 5, 10, 15, 20, 50; 73)= F (1,2,3,5,10,15,20;73)+ F (1,2,3,5,10,15,20; 23).

Первый член равен 0, так как сумма оставшихся монет меньше набираемой суммы.

Применим ту же рекуррентную формулу к оставшемуся члену. В результате получим:

F (1, 2, 3, 5, 10, 15, 20; 23) = F (1, 2, 3, 5, 10, 15; 3) + F (1, 2, 3, 5, 10, 15; 23)

В первом члене правой части монеты достоинством в 5, 10 и 15 копеек можно не учитывать, так как достоинство каждой из этих монет больше набираемой суммы, т. е. можно правую часть переписать так:

F (1, 2, 3; 3) + F (1, 2, 3, 5, 10, 15; 23) =

= F (1, 2; 0) + F (1, 2;3 ) + F (1, 2, 3, 5, 10; 8) + F (1, 2, 3, 5, 10; 23) = = 1+ F (1; 1) + F (1; 3) + F (1, 2, 3, 5; 8) + F (1, 2, 3, 5, 10; 23).

Очевидно, что F (1, 2; 0) = 1; F (1, 2; 3) = F (1;1) = 1; F (1; 3) = 0;

F (1, 2, 3, 5, 10; 23) = 0. Поэтому правая часть перепишется в виде:

1 + 1 + 0 + F (1, 2, 3, 5; 8) + 0 = 2 + F (1, 2, 3; 3) + F (1, 2, 3; 8) = 2 + 2 + 0 = 4.

Таким образом, задача имеет 4 различных решения. Подчеркнем еще раз, что в этой задаче порядок монет не важен.

17.2.3 Задача о размене гривенника (10 копеек)

Рассмотрим задачу, в которой сняты ограничения, как на порядок предметов, так и на их количество: размен гривенника монетами достоинством в 1, 2, 3, 5 копеек.

Для этого случая рекуррентное соотношение имеет вид

S (1, 2, 3, 5; 10) = S (1, 2, 3; 10) + S (1, 2, 3; 5) + S (1, 2, 3; 0).

Таким образом, все множество решений разбивается на подмножества в зависимости от числа монет старшего достоинства, использованных для

размена.
Находим все 20 способов размена:
5*2;	5+1*5;	3+2*3+1;	2*4+1*2;
5+3+2;	3*3+1;	3+2*2+1*3;	2*3+1*4;
5+3+1*2;	3*2+2*2;	3+2+1*5;	2*2+1*6;
		159

5+2*2+1;	3*2+2+1*2;	3+1*7;	2+1*8;
5+2+1*3;	3*2+1*4;	2*5;	1*10.

17.3 Контрольные вопросы и задания

1.Дайте определение продуктивной функции

2.Дайте определение экспоненциальной продуктивной функции.

3.Приведите примеры задач, которые решаются с использованием рекуррентных соотношений в комбинаторике.

4.Дайте характеристику задачи о наклейке марок.

5.Каким образом может быть решена задача об уплате долга?

6.Дайте характеристику задачи о размене гривенника (10 копеек).

ЛЕКЦИЯ 18. ПРОИСХОЖДЕНИЕ ГРАФОВ. ОПРЕДЕЛЕНИЕ ГРАФОВ

18.1 Разновидности графов. Неориентированный граф. Определения

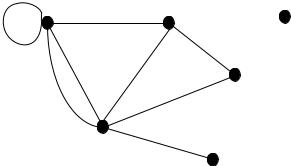
Определение. Граф или неориентированный граф G (рис. 18.1) – это упорядоченная пара G : (V , E) , для которой выполнены следующие условия:

V – это непустое множество вершин или узлов,

E – это множество пар (в случае неориентированного графа – неупорядоченных) вершин, называемых рѐбрами.

h	1	a	2

6

	b
	e
	d
g	3

c

4

f

5

Рисунок 18.1 – Неориентированный граф

V (а значит и E , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные

160