ДМ_Конспект

Для множеств X {1, 2, 3, 4} и Y {1, 4, 9,16, 25} отношение B {(1,1), (2, 4), (3, 9), (4,16)}, имея различные первые координаты, также

является функциональным.

Всякое функциональное отношение можно рассматривать как функцию.

Определение

Бинарное отношение

f X Y

называется

функцией,

или

отображением, из множества

X

в множество Y , если область определения

функции DO f

X ,

область значений

функции

DЗ f Y

и

из

(x, y1 ) f ,

(x, y2 ) f

следует,

что y1

y2 . Функция f

из множества

X

в множество Y

обозначается

f : X Y или X Y .

f

Если

вместо

DO f

X

выполняется

DO f

X ,

то

f

называется

частичной функцией.

Определение

Если

множество

A X ,

то

через

f (A) {y Y | y f (x), x A}

обозначается образ множества

A . Множество

f ( X ) Y

называется образом

или областью значений отображения f

и обозначается DЗ f f ( X ) .

Если

множество

B Y , то

множество

f 1 (B) {x X | f (x) B}

называется

прообразом множества B относительно отображения

f .

Однако следует различать функцию f

как множество упорядоченных пар

(отношение)

и значение функции

y f (x)

как вторую координату одной из

таких пар.

Для

всякого

функционального

отношения

F

можно

определить

связанную с этим отношением функцию, но симметричное к нему отношение

F 1 может не быть функцией.
Пример.	Пусть	задано	функциональное	отношение

F {(x1 , y1 ), (x2 , y2 ), (x3 , y1 ), (x5 , y3 ), (x6 , y1 )}.

Так, отношение	F 1 {( y , x ), ( y		2	, x	2	), ( y , x ), ( y			, x ), ( y , x )}, обратное
	1	1				1	3	3	5	1	6

рассмотренному отношению, не является функцией, так как имеют одинаковые первые координаты.

Существуют следующие основные типы отображений (функций):

сюръекция (функция, сюръективное отображение X на Y );

инъекция (инъективная функция, инъективное отображение X на Y );

биекция (биективная функция, биективное отображение X на Y , взаимнооднозначное соответствие).

Определение

Функция f : X Y называется сюръективной функцией

(сюръективным отображением), если DЗ f Y . Для сюръективной функции

для любого y Y	существует x X такой, что	f (x) y .
	51

На графе, представляющем сюръективное отображение f : X Y , из

любой вершины x X выходит в точности одна дуга, а в любую вершину, представляющую элемент множества Y , входит не менее одной дуги.

Пример.

Сюръективное отображение X на Y , заданное в виде графа, представлено на рис. 5.1.

x1

y1

x2

y2

x3

y3

x4

Рисунок 5.1 Сюръективное отображение X на Y , представленное в виде графа

Определение
Функция f : X Y			называется инъективной функцией (инъективным
отображением), если для любых элементов xi , x j DO f из				xi x j следует
f (x ) f (x		) (отношение	f 1 является частичной функцией).
i	j
На	графе, представляющем инъективное отображение			f : X Y , из

любой вершины x X выходит в точности одна дуга, а в любую вершину, представляющую элемент множества Y , входит не более одной дуги.

Пример.
Инъективное отображение, заданное в виде	графа, представлено на
рис. 5.2.
y1
x1
y2
x2
y3
x3
y4
Рисунок 5.2 Инъективное отображение X на Y , представленное в виде графа
Определение
Функция f : X Y называется биективной	функцией (биективным

отображением), если она одновременно сюръективна и инъективна. Биективное отображение f : X Y осуществляет взаимнооднозначное

отображение между множествами X и Y , поэтому X ~ Y , | X | | Y |.

Свойство биективности обеспечивает существование обратного отображения. Это означает, что если f : X Y биективно, то существует

обратное отображение f 1 :Y X , причем DO f 1 Y .

52

На графе, представляющем биективное отображение f : X Y конечных

множеств, их любой вершины x X выходит в точности одна дуга, а в любую вершину, представляющую элемент множества Y , входит одна и только одна дуга.

Пример. Биективное отображение X на Y , заданное в виде графа, представлено на рис. 5.3.

y1

x1

y2

x2

y3

x3

Рисунок 5.3 Биективное отображение X на Y , представленное в виде графа

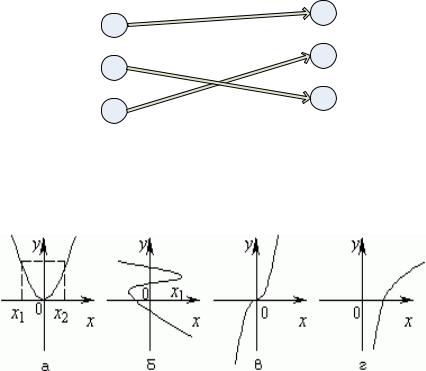
Пример. Дадим характеристику свойств соответствий, представленных на рис. 5.4:

Рисунок 5.4 Соответствия f

а соответствие f всюду определено, не сюръективно, не инъективно, функционально, не является биективным, f является отображением, так как оно всюду определено и функционально;

б соответствие f	всюду определено, сюръективно, не функционально;
в соответствие	f является биективным, а значит функцией и

отображением; г частичное соответствие, сюръективно, инъективно, функционально

(однозначно), но не является отображением.

Пример.

Различные виды кодирования (кодирование букв азбукой Морзе, представления чисел в различных системах счисления, секретные шифры, входящие и исходящие номера в деловой переписке и т.д.) являются соответствиями между кодируемыми объектами и присваиваемыми им кодами. Эти соответствия, как правило, обладают всеми свойствами взаимнооднозначного соответствия, кроме, возможно, одного сюръективности. Единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки. Отсутствие сюръективности означает, что не каждый

53

код имеет смысл. Например, кодирование телефонов шестизначными номерами не сюръективно, поскольку некоторые номера не соответствуют никаким телефонам. Для кодирующей функции, которая каждому объекту из своей области значений ставит в соответствие некоторый код, обратной будет декодирующая функция, которая каждому коду ставит в соответствие закодированный этим кодом объект. Если кодирующая функция не сюръективна, то декодирующая функция не всюду определена.

5.2 Элементы реляционной алгебры

Алгебра отношений находит широкое применение при формализации реальных объектов. Рассмотрим специфику еѐ использования при создании элементов внутримашинного информационного обеспечения разработке информационной базы данных. Алгебра отношений в данном случае носит название реляционной алгебры (relation отношение) и применяется для работы с реляционной моделью данных. Реляционная модель данных с математической точки зрения является табличным представлением данных, которое легко формулируется в терминах отношений.

Рассмотрим отношение R , заданное на множествах X1 , X 2 , ..., X n ,

которое при работе с реляционными базами данных задается на конечных множествах и поэтому является конечным. Основой построения реляционной базы данных (реляционной модели данных) является отношение R , представленное в виде двумерной таблицы (с именем R ) размером m n , где m мощность отношения, а n его арность. Каждый столбец данной таблицы соответствует домену (или атрибуту, соответствующему части домена),

строка кортежу значений атрибутов, находящихся в отношении					R (или
записи отношения R ).
Пример. Пусть имеется информация о студентах университета,
представленная в следующей таблице.
	Фамилия		Инициалы	Группа
	Алексеев		И.А.	ПО-01
	Андреева		О.П.	ПМ-01
	Баранов		Н.П.	ПМ-01
	Быкова		Н.А.	ПО-01
	Волков		В.В	ПМ-01
Эта информация представляет собой некоторое отношение R1 ,					заданное

на трех множествах: множестве фамилий, множестве инициалов и множестве групп. Отношение R1 можно записать списком его элементов, т.е. {(Алексеев,

И.А., ПО-01), (Андреева, О.П., ПМ-01), (Баранов, Н.П., ПМ-01), (Быкова, Н.А., ПО-01), (Волков, В.В, ПМ-01)}. Отношению присваивают имя, например, СТУДЕНТ_1.

54

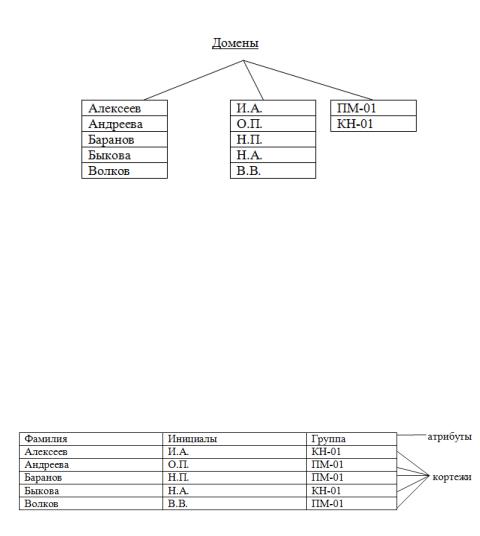
Рассмотрим терминологию, применяемую при построении реляционной модели данных.

Определение.

Если (x1 , x2 ,...,xn ) R X1 X 2 ... X n , то				элемент	(x1, x2 ,...,xn ) ,
соответствующий строке таблицы, называется кортежем (записью).
Пример.
Кортежами являются такие элементы отношения R1 , как (Алексеев, И.А.,
ПО-01), (Андреева, О.П., ПМ-01), (Баранов, Н.П., ПМ-01) и т.п.
Определение.
Множества	или	области данных	X i , которые	входят в	произведение
X1 X 2 ... X n ,	т.е.	на которых	определено отношение,		называются

доменами.

Пример.

Доменами отношения R1 , представленными на рис. 5.5, являются:

множество фамилий, множество инициалов и множество групп, соответствующие столбцам таблицы.

Рисунок 5.5 Домены отношения

Определение.

Наименования столбцов таблицы называют атрибутами.

Пример.

Атрибутами отношения СТУДЕНТ_1 являются: фамилия, инициалы, группа.

Представим это отношение на рис. 5.6.

Рисунок 5.6 Отношение СТУДЕНТ_1

55

Определение. Схемой отношения является список атрибутов.

Пример.

Схемой отношения СТУДЕНТ_1 является список (Фамилия, Инициалы, Группа).

Для изменения содержимого таких таблиц (реляционных таблиц) в базах данных используются простые следующие операции по заполнению таблицы: добавление, удаление кортежей, изменение значения атрибутов.

Основная идея реляционной алгебры Ap (M , ) заключается в

следующем. Поскольку отношения являются множествами, то средства манипулирования отношениями могут базироваться на таких традиционных теоретико-множественных операциях, как объединение, пересечение, разность, декартово произведение, дополненных некоторыми специальными операциями. Следовательно, носитель реляционной алгебры представляет собой множество отношений M {R1 , R2 , ..., Rk }, сигнатура {1 ,2 ,...,m ,..} кроме операций

объединения, пересечения, разности, декартова произведения включает специальные операции над отношениями: ограничение отношений (выбор),

проекцию отношений, соединение отношений, деление отношений.

В соответствии с потребностями практики вводятся и некоторые другие операции.

Рассмотрим теоретико-множественные операции, применяемые для преобразования отношений в базе данных, используя термины реляционной алгебры.

Определение. Отношения, к которым применяется операция, будем называть отношениями-операндами.

Ктеоретико-множественным операциям реляционной алгебры относятся:

объединение отношений;

пересечение отношений;

разность отношений;

прямое (декартово) произведение отношений.

Эти операции имеют смысл для отношений, определенных на одинаковых доменах.

Определение. Объединение отношений ( ). При выполнении операции объединения двух отношений получаем отношение, включающее все кортежи, входящие хотя бы в одно из отношений-операндов.

Пример. Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2. СТУДЕНТ_1

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Быкова	Н.А.	КН-01
Волков	В.В	ПМ-01
	56

СТУДЕНТ_2

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Быкова	Н.А.	КН-01
Дроздов	И.К.	КН-01
Зайцев	О.Н.	ПМ-01
Кузнецова	Е.В	КН-01

Применим операцию объединения к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В результате получим следующее отношение (ВСЕ_СТУДЕНТЫ).

ВСЕ_СТУДЕНТЫ=СТУДЕНТ_1 СТУДЕНТ_2

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Быкова	Н.А.	КН-01
Волков	В.В	ПМ-01
Дроздов	И.К.	КН-01
Зайцев	О.Н.	ПМ-01
Кузнецова	Е.В	КН-01

Определение.

Пересечение отношений ( ). При выполнении операции пересечения двух отношений получаем отношение, включающее только те кортежи, которые входят в оба отношения-операнда.

Пример.

Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2 (из предыдущего примера). Применим операцию пересечения к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В	результате		получим	следующее		отношение
(СТУДЕНТ_1 СТУДЕНТ_2).
		СТУДЕНТ_1 СТУДЕНТ_2
	Фамилия		Инициалы		Группа
	Алексеев		И.А.		КН-01
	Быкова		Н.А.		КН-01

Определение.

57

Разность отношений (\). Отношение, являющееся разностью двух отношений, включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом.

Пример.

Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2 (из предыдущего примера). Применим операцию (\) к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В результате получим следующее отношение (СТУДЕНТ_1\СТУДЕНТ_2).

СТУДЕНТ_1\СТУДЕНТ_2

Фамилия	Инициалы	Группа
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Волков	В.В	ПМ-01

Определение.

Прямое (декартово) произведение отношений ( ). При выполнении прямого произведения двух отношений получаем отношение, множество кортежей которого является декартовым произведением множеств кортежей первого и второго операндов.

Пример.

Рассмотрим отношение СТУДЕНТ_1 (из предыдущих примеров) и КУРС. КУРС

Уч. год	Курс
2009-2010	1
2010-2011	2

Выполним прямое произведение отношения СТУДЕНТ_1 и КУРС.

В результате получим следующее отношение (СТУДЕНТ_1 КУРС).

СТУДЕНТ_1 КУРС

Фамилия	Инициалы	Группа	Уч. год	Курс
Алексеев	И.А.	КН-01	2009-2010	1
Алексеев	И.А.	КН-01	2010-2011	2
Андреева	О.П.	ПМ-01	2009-2010	1
Андреева	О.П.	ПМ-01	2010-2011	2
Баранов	Н.П.	ПМ-01	2009-2010	1
Баранов	Н.П.	ПМ-01	2010-2011	2
Быкова	Н.А.	КН-01	2009-2010	1
Быкова	Н.А.	КН-01	2010-2011	2
Волков	В.В	ПМ-01	2009-2010	1
Волков	В.В	ПМ-01	2010-2011	2
		58

Далее рассмотрим специальные операции реляционной алгебры, применяемые в базах данных. К таким операциям следует отнести:

ограничение отношений;

проекция отношений;

естественное соединение отношений;

деление отношений.

Определение.

Ограничение отношений ( ). Результатом ограничения отношения по некоторому атрибуту или атрибутам является отношение, состоящее в точности из тех кортежей, которые удовлетворяют условию .

Пример.

Выполним ограничение отношения ВСЕ СТУДЕНТЫ по атрибуту Группа=КН-01. Результат назовем СТУДЕНТ_КН-01. В результате получим

отношение Группа КН 01 (ВСЕ			СТУДЕНТЫ)=СТУДЕНТ_КН-01, содержащее
только кортежи, в которых значение атрибута Группа равняется КН-01.
		СТУДЕНТ_КН-01
	Фамилия		Инициалы	Группа
	Алексеев		И.А.	КН-01
	Быкова		Н.А.	КН-01
	Дроздов		И.К.	КН-01
	Кузнецова		Е.В	КН-01

Определение.

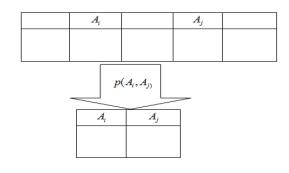
Проекция отношения ( ). При выполнении проекции отношения на заданный набор его атрибутов отношение-результат получается путем удаления из отношения-операнда атрибутов, не указанных в заданном наборе.

Схематически выполнение операции представлено на рис. 5.7.

Рисунок 5.7 Схема выполнения операции проекции по Ai , Aj

Пример. Выполним проекцию отношения СТУДЕНТ_1_КУРС по атрибутам Группа, Уч. год, Курс.

Группа,Уч.год,Курс ( СТУДЕНТ_1_КУРС)

Группа	Уч. год	Курс
КН-01	2009-2010	1
КН-01	2010-2011	2
ПМ-01	2009-2010	1
	59

ПМ-01

2010-2011

2

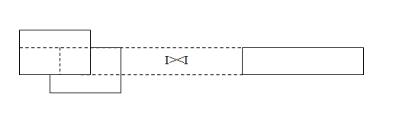
Определение. Естественное соединение отношений (І><I). При естественном соединении двух отношений образуется результирующее отношение, кортежи которого являются соединением кортежей первого и второго отношений, если значение общих атрибутов совпадает.

Схематически выполнение операции І><I представлено на рис. 5.8.

Рисунок 5.8 Схема выполнения операции естественного соединения отношений

Пример. Пусть задано отношение НОМЕР НОМЕР

Фамилия	Инициалы	Зачетка №	Студ. №
Алексеев	И.А.	11197	784567
Андреева	О.П.	11215	784565
Баранов	Н.П.	11213	784598
Быкова	Н.А.	11216	784588
Волков	В.В	11217	784599
Дроздов	И.К.	11193	784611
Зайцев	О.Н.	11191	784601
Кузнецова	Е.В	11195	785587

Выполним естественное соединение отношений СТУДЕНТ_КН-01 и НОМЕР. СТУДЕНТ_КН-01 І><I НОМЕР

Фамилия	Инициалы	Группа	Зачетка №	Студ. №
Алексеев	И.А.	КН-01	11197	784567
Быкова	Н.А.	КН-01	11216	784588
Дроздов	И.К.	КН-01	11193	784611
Кузнецова	Е.В	КН-01	11195	785587

Определение.

Деление отношений ( ). Операция деления отношений осуществляется следующим образом. Отношение-делитель должно иметь набор атрибутов, включенный в набор атрибутов делимого. Результирующее отношение содержит те атрибуты делимого, которые не присутствуют в делителе. Значения этих атрибутов берутся из тех кортежей делимого, которые включают в себя кортежи делителя.

60