ДМ_Конспект

(v1,v2 ) смежны в графе G1			тогда и только тогда, когда или u1 v1 , а u2 и v2
смежны в G2 , или u2 v2 , а u1 и v1				смежны в G1 .
				(1,u)	(1,v)	(1,w)
			u
1	2	*	v	=
			w
				(2,u)	(2,v)	(2,w)

Рисунок 19.11 – Декартово произведение графов

19.2 Гомеоморфные графы

Два графа называются гомеоморфными или тождественными с точностью до вершины степени 2, если они могут быть получены из одного и того же графа с помощью операции ведения вершины степени 2 в ребро. На рисунке 19.12 показаны гомеоморфные графы.

а

б

Рисунок 19.21 – Гомеоморфные графы

19.3 Плоские и планарные графы

Все изображения графа являются изоморфными и несут одну и ту же информацию. Однако встречаются ситуации, когда крайне важно, чтобы изображение графа на плоскости удовлетворяло определенным требованиям.

Например, в радиоэлектронике при изготовлении микросхем печатным способом электрические цепи наносятся на поверхность изоляционного материала. А так как проводники не изолированы, то они не должны пересекаться. Аналогичная задача возникает при проектировании железнодорожных и иных путей, где нежелательны переезды.

181

Определение. Геометрический граф назовем плоским графом, если он нарисован на плоскости так, что все линии, изображающие его ребра, пересекаются только в точках, соответствующих вершинам графа, т.е. любая точка пересечения таких линий, есть вершина, инцидентная ребрам, которые эти линии изображают. Любой граф, изоморфный плоскому графу, называют

планарным.

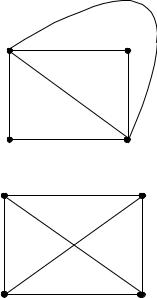
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку) (рис. 19.22). Планарный граф можно уложить на плоскости, а плоский граф – это граф, уже уложенный на плоскости. Плоский граф есть изображение планарного графа, однако не каждое изображение планарного графа является плоским графом.

1

2

3	4

G1

Рисунок 19.22 – Плоский граф

1

2

3

4

G2

Рисунок 19.23 – Планарный граф

Пример плоского графа приведен на рис. 19.22. Изоморфный ему полный граф K4 (рис. 19.23), укладываемый на плоскости, имеет два пересекающихся ребра, поэтому граф K4 не является плоским – он только планарный.

19.3.1 Теорема Понтрягина – Куратовского

Теорема Понтрягина – Куратовского гласит: граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 и K3,3 , где K5 – полный 5-вершинный граф, а K3,3 – полный двудольный граф, каждая доля которого состоит из 3 вершин. Граф K5 представляет собой полный граф

182

наименьшего порядка, который, не являясь планарным графом (полные графы K2 , K3 , K4 – планарные), становится планарным после удаления хотя бы одного его ребра. Второй (двудольный граф K3,3 ) является моделью известной задачи о трех домах и трех колодцах.

1

2

5

3 4

K5

Рисунок 19.24 – K5 – полный 5-вершинный граф

	3	4
	1
	1
2	5	6
	K3,3

Рисунок 19.25 – K3,3 – полный двудольный граф

Определение. Жордановой кривой на плоскости называется непрерывная кривая линия без самопересечений. Замкнутая жорданова кривая – это жорданова кривая, начало и конец которой совпадают.

	2	1	2
1

1	2

G1	G3
G2
Рисунок 19.26 – Примеры жордановых кривых
Теорема Жордана: Если S замкнутая	жорданова кривая, то всякая

жорданова кривая, соединяющая точки 1 и 2, лежащие на S , либо полностью лежит внутри S (рис. 19.26 граф G1 ), либо вне S (рис. 19.26 граф G2 ), либо пересекает S в одной единственной точке отличной от 1 и 2 (рис. 19.26 граф G3 ).

183

19.3.2 Построение плоского изображения графа. Гамма-алгоритм

Для плоской укладки графа и попутной проверки, планарный ли он, удобно пользоваться гамма-алгоритмом.

На вход подаются графы, обладающие следующими свойствами:

1.Граф связный.

2.Граф имеет хотя бы один цикл.

3.Граф не имеет мостов, т. е. ребер, после удаления которых граф распадается на две компоненты связности.

Если нарушено свойство (1), то граф нужно укладывать отдельно по компонентам связности.

Если нарушено свойство (2), то граф – дерево и нарисовать его плоскую укладку тривиально.

Случай нарушения свойства (3) рассмотрим более подробно. Если в графе есть мосты, то их нужно разрезать, провести отдельно плоскую укладку каждой компоненты связности, а затем соединить их мостами. Здесь может возникнуть трудность: в процессе укладки концевые вершины моста могут спрятаться внутри плоского графа. Нарисуем одну компоненту связности и будем присоединять к ней другие последовательно. Каждую новую компоненту связности будем рисовать в той грани, в которой лежит концевая вершина соответствующего моста. Так как граф связности мостами компонент связности является деревом, мы сумеем получить плоскую укладку.

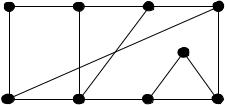
Сначала рассмотрим алгоритм на конкретном примере. Пусть дан граф G

(рис. 19.27).

1

2

3

4

9

8	7	6	5

G

Рисунок 19.27 Инициализация алгоритма производится так: выбираем любой простой

цикл; в нашем примере {1, 2, 3, 4, 5, 6, 7, 8} и получаем две грани: a1 – внешнюю и a2 – внутреннюю (см. рис. 19.28).

184

1	2	3	4
a1	a2

8	7	6	5

G

Рисунок 19.28

Обозначим выбранный цикл как G . На каждом шаге будем строить множество сегментов. Каждый сегмент S относительно уже построенного графа G представляет собой одно из двух:

ребро, оба конца которого принадлежат G , но само оно не принадлежит G ;

связную компоненту графа G G , дополненную всеми ребрами графа G , один из концов которых принадлежит связной компоненте, а второй из

графа G .

Те вершины, которые одновременно принадлежат G и какому-то сегменту, назовем контактными. Для нашего примера сегменты и вершины изображены на рис. 19.29. Контактные вершины обведены в квадрат.

4 7 7 9

8		2	3	5	6
S1	S2	S3			S4

Рисунок 19.29

Если бы в каком-нибудь сегменте не было ни одной контактной вершины, то граф до разрезания был бы несвязный; если бы была только одна, то граф имел бы мост. Эти возможности заранее исключены, так что каждый сегмент имеет не менее двух контактных вершин. Поэтому в каждом сегменте имеется цепь между любой парой таких вершин.

Если все контактные вершины сегмента S имеют номера вершин какойто грани a , то мы будем говорить, что грань a вмещает этот сегмент и обозначать S a . Может быть имеется не одна такая грань, вмещающая сегмент S , множество таких граней обозначим a(S) , а их число a(S) .

185

Общий шаг алгоритма следующий: обозреваются все сегменты Si и определяются числа a(Si ) . Если хоть одно из них равно 0, то граф не планарен,

конец. Иначе, выбираем сегмент, для которого число a(S) минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества а(S), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа G по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам G .

В результате повторения общего шага либо будет получена плоская укладка, когда множество сегментов станет пустым, либо будет получено, что

граф G не является планарным. Вернемся к нашему примеру.
Пока	i : Si {a1,a2}, a(Si ) 2 .			Поэтому возьмем			первый		по номеру
сегмент Si	и в нем первую попавшеюся цепь {4, 8}; вставим эту цепь в грань a2
Получим	увеличенную	часть G		и	уменьшенную		систему		сегментов
(см. рис. 19.30 А), В)).
1	2		3	4	7	7	9
a1	a2
			a3
8	7		6	5	2	3	5	6
		G	A)		S1	S2		S3	B)

Рисунок 19.30

Определим, какие грани вмещают новые сегменты. Теперь сегменты S1 и S2 вмещаются только в одну грань a1 , в то время, как сегмент S3 вмещается в две грани а1 и а3. Поэтому берем S1 . Возьмем в нем цепь между контактными вершинами, например, {2, 7}, и уложим ее в a1 . Получим увеличенную часть G и уменьшенную систему сегментов (рис. 19.31 А), В)).

186

1

2

3

4

7

9

a	a4	a2
1
	8	7

a3

6

5

3

5

6

G	A)	S1	S2	B)

Рисунок 19.31

Продолжая таким образом, в итоге получим плоскую укладку G (рис. 19.32).

	1	2	3		4
a1		a2		9
	a4
			a3
			G
	8	7	6	5	a6

G

Рисунок 19.32

19.3.3 Гамма-алгоритм (в общем виде)

1. (Инициализация). Выберем любой простой цикл C исходного графа G ; изобразим его на плоскости в виде грани, которую примем за уже уложенную часть G ; сформируем сегменты Si ; если множество сегментов пусто, то перейти к п. 3.

2.(Общий шаг). Пока множество сегментов непустое:

a. Для каждого сегмента S найти множество a(S) . Если

существует сегмент S , для которого a(S) 0 , то граф не планарный, конец.

b.Выбираем один из сегментов с минимальным числом, вмещающих его граней.

c.Выбираем одну из подходящих граней для выбранного

сегмента.

d.В данном сегменте выбираем цепь между двумя контактными вершинами и укладываем ее в выбранной грани. Учтем изменения в структуре сегментов и перейдем к п. a).

3.(Завершение). Построена плоская укладка G исходного графа G ,

конец.

187

9.4 Контрольные вопросы и задания

1.Перечислите операции, которые можно производить над графами.

2.Охарактеризуйте операции удаления ребер и вершин.

3.Какой граф называется дополнением графа G (V , X1 ) ?

4.Как определить композицию G1 (G2 ) графов G1 и G2 . Приведите

пример.

5.Дайте характеристику операции соединения (сильного произведения)

графов.

6.Какие графы называются гомеоморфными графами.

7.Какие графы называются изоморфными графами.

8.Дайте определения плоского графа, планарного графа.

9.Для решения каких задач можно использовать теорему Понтрягина – Куратовского?

10.Для решения каких задач можно использовать теорему Жордана?

11.Для плоской укладки графа и попутной проверки, планарный ли он, можно использовать гамма-алгоритм?

12.Приведите гамма-алгоритм в общем виде.

ЛЕКЦИЯ 20. СВЯЗНОСТЬ ГРАФОВ. ЭЙЛЕРОВЫ И ГАМИЛЬТОНОВЫ

ГРАФЫ

20.1 Связность графов, компонента связности. n-связный граф

Определение. Две вершины v и w в графе связны, если существует соединяющая их (простая) цепь. Если же в графе нет ни одной цепи, соединяющей вершины v и w , то вершины v и w являются несвязными.

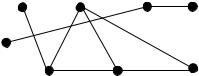
Пример. Вершины 1 и 5 (рис. 20.1) связны, так как их соединяет цепь

1,7,6,5 (а также 1,7,2,5; 1,7,6,2,5 и 1,7,2,6,5), а вершины 2 и 3 связными не являются, так как ни одна цепь их не соединяет.

1	2	3	4
8
	7	6	5
	Рисунок 20.1
		188

Определение. Граф называется связным, если любая пара его вершин связана. Если же в графе имеется хотя бы одна пара вершин, не соединенных цепью, то граф называется несвязным.

Пример. Согласно этим определениям граф, изображенный на рис. 20.1, является несвязным, а граф, приведенный на рис. 20.2, – связным.

1	2	3
4	5	6

Рисунок 20.2

Отношение связности вершин v и w является рефлексивным (всякая вершина, имеющая петлю, связна сама с собой), симметричным (если вершины

vи w связны, то связны и вершины w и v ), транзитивным (если вершины v и

wсвязны и связны вершины w и t , то связны и вершины v и t ), следовательно, множество связных вершин образует класс эквивалентности.

Определение. Классы эквивалентности, из которых состоит несвязный граф, называются его компонентами. Между разными компонентами связности ребер нет.

Любой связный граф состоит из одной компоненты связности – всего графа.

Определение. Число компонент, из которых состоит граф, называется степенью связности. Число компонентов связности графа G обозначается

k(G) .

Пример. Граф, изображенный на рисунке 20.2, имеет степень связности, равную 2. Степень связности графа, приведенного на рис. 20.3, равна 5.

1		2	3	4

8

7

6

5

Рисунок 20.3

Определение. Граф называется n-связным, если между любыми его двумя вершинами найдется n цепей, попарно не имеющих общих неконцевых вершин.

189

Определение. Числом вершинной связности (или просто числом связности) (G) графа G называется наименьшее число вершин, удаление которых приводит к несвязному или одновершинному графу.

Определение. Пусть G – граф порядка n 1. Числом реберной связности (G) графа G называется наименьшее число ребер, удаление которых приводит к несвязному графу.

Определение. Вершина v графа G называется точкой сочленения (или разделяющей вершиной), если граф G \ v имеет больше компонент, чем G . В частности, если G связен и v – точка сочленения, то G \ v несвязен. Аналогично ребро графа называется мостом, если его удаление увеличивает число компонент. Концевая вершина моста является точкой сочленения, если в графе есть другие ребра, инцидентные этой вершине.

20.2 Свойства связных графов

1.Связный граф остается связным после удаления ребра тогда и только тогда, когда это ребро содержится в цикле.

2.Связный граф, имеющий n вершин, содержит по крайней мере n 1

ребро.

3.В связном графе любые две простые цепи максимальной длины имеют по крайней мере одну общую вершину.

4.Пусть у графа G есть n вершин. Пусть D(G) – минимальная из

степеней вершин этого графа. Тогда D(G) 12 (n 1) .

20.3 Компоненты сильной связности ориентированного графа

Определение. Орграф называется сильно связным (strongly connected),

если любые две его вершины сильно связаны. Две вершины s и t любого графа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s. Сильно связными компонентами орграфа называются его максимальные по включению сильно связные подграфы.

Для нахождения компонент сольной связности в орграфе cоставляем матрицу смежности A(D) размерности n n (n − количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк

– индексы вершин, из которых исходят дуги, номера столбцов – индексы

190