
ДМ_Конспект
.pdf
Пример. Сколько разных чисел может содержать 10-разрядное слово в троичной системе счисления? В первый разряд можно поставить один из трех символов (0, 1 или 2), во второй разряд – также один из трех символов и т. д. Всего получаем A103 310 чисел.
14.3.3 Перестановки без повторений
В предыдущих параграфах комбинации отличались как составом предметов, так и их порядком. Однако если в последней задаче юношей было бы тоже 12, то все комбинации отличались бы только порядком.
Рассмотрим, сколько различных комбинаций можно получить,
переставляя |
n |
предметов. |
Положим |
n k |
в |
формуле |
||
A n n 1 n 2 ... n k 1 n! |
n k ! |
, тогда получим An P n!. |
|
|||||
|
|
|
|
n |
n |
|
||
|
|
|
|
|
|
|
||
Пример. К кассе кинотеатра подходит 6 человек. Сколько существует различных вариантов установки их в очередь друг за другом?
Расставим 6 человек произвольным образом и начнем их переставлять всеми возможными способами. Число полученных перестановок в соответствии с формулой (5.3) будет равно 6! = 720.
14.3.4 Перестановки с повторениями
Иногда требуется переставлять предметы, некоторые из которых неотличимы друг от друга. Рассмотрим такой вариант перестановок, который
называется перестановками с повторениями. |
|
|
||||
Пусть имеется n1 |
предметов 1-го типа, n2 |
предмета 2-го, nk |
предметов k - |
|||
го типа и при этом |
n1 n2 ... nk n . Количество разных |
перестановок |
||||
предметов равно P n , n ,..., n |
n! |
n1!n2 !...nk ! |
. |
|
||
1 |
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
Для обоснования данной формулы сначала будем переставлять n предметов в предположении, что они все различны. Число таких перестановок равно n!. Затем заметим, что в любой выбранной расстановке перестановка n1 одинаковых предметов не меняет комбинации, аналогично перестановка n2 одинаковых предметов также не меняет комбинации и т. д. Поэтому получаем выражение P n1, n2 ,..., nk n! n1!n2 !...nk ! .
141

Пример. Найдем количество перестановок букв слова КОМБИНАТОРИКА. В этом слове 2 буквы к, 2 буквы о, 1 буква м, 1 буква б, 2 буквы и, 1 буква н, 2 буквы а, 1 буква т и 1 буква р.
Таким образом, число перестановок букв этого слова равно:
P(2, 2, 1, 1, 2, 1, 2, 1, 1) = 13!/(2! 2! 2! 2!)= 13!/16.
14.3.5 Сочетания без повторений
Если |
требуется выбрать k предметов |
из n , |
и при |
этом порядок |
||||
выбираемых предметов безразличен, то имеем |
Ck |
n! |
. |
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
n |
k!(n |
k)! |
|
|
|
|
|
|
|
|
|
|
|||
Эта формула может быть получена следующим образом. Выберем по |
||||||||
очереди k |
предметов из n. Число вариантов будет равно n! |
(n k)! |
. В этих |
|||||
|
|
|
|
|
|
|
|
|
расстановках k выбранных предмета имеют свои определенные позиции. Однако нас не интересуют в данном случае позиции выбранных предметов. От перестановки этих предметов интересующий нас выбор не меняется. Поэтому полученное выражение нужно разделить на k !
Пример. Из группы в 25 человек нужно выбрать троих для уборки помещения. Если выбирать их последовательно, сначала первого, потом второго, потом третьего, то получим 25 24 23 варианта. Но так как нас не интересует порядок выбора, а только состав выбранной бригады, поэтому полученный результат нужно разделить еще на 3!
Пример. В середине 60-х годов в России появились две лотереи, которые по недоразумению были названы ―Спортлото‖: лотерея 5/36 и 6/49. Рассмотрим 6/49. Играющий покупает билет, на котором имеется 49 клеточек. Каждая клеточка соответствует какому-либо виду спорта. Нужно выделить (зачеркнуть) 6 из этих клеточек и отправить организаторам лотереи. После розыгрыша лотереи объявляются шесть выигравших номеров. Награждается угадавший все шесть номеров, пять номеров, четыре номера и даже угадавший три номера. Соответственно, чем меньше угадано номеров (видов спорта), тем меньше выигрыш.
Подсчитаем, сколько существует разных способов заполнения карточек ―Спортлото‖ при условии, что используется лотерея 6/49. Казалось бы, заполняя последовательно номер за номером, получим: 49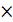 48
48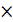 47
47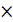 46
46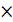 45
45 44.
44.
Но ведь порядок заполнения не имеет значения, тогда получаем:
142

Cnk 6!43!49! 13983816 .
Эту же задачу можно решить и другим способом. Выпишем все номера подряд и под выбираемыми номерами поставим 1, а под остальными – 0. Тогда различные варианты заполнения карточек будут отличаться перестановками. При этом переставляются 6 предметов одного вида (единицы) и 49 – 6 = 43
предмета другого вида (нули), т. е. опять P 6,43 6!43!49! 13983816.
Если все участники заполняют карточки по-разному, то в среднем один из примерно 14 миллионов угадает все 6 номеров. А сколько человек в среднем угадают 5 номеров?
Выберем один из угаданных номеров (C61 6) и заменим его на один из не угаданных C431 43 . Итого: 6 43 = 258 человек из 14 миллионов угадают 5
номеров. А сколько угадают 4 номера? Выберем из 6 угаданных два и затем из 43 не угаданных тоже два и перемножим число вариантов выбора. Тогда
получим: C1 |
C1 |
|
6 5 |
|
43 42 |
13545 человек. |
|
|
|||||
6 |
6 |
|
1 2 |
|
1 2 |
|
|
|
|
|
|||
Аналогично найдем, что 3 номера угадают 246820 человек, т. е. примерно 1,77% от всех играющих.
14.3.6 Сочетания с повторениями
Пример. Требуется купить 7 пирожных. В магазине имеются пирожные следующих видов: эклеры, песочные, слоеные и наполеоны. Сколько вариантов выбора? Решение: выбранные пирожные заменяем единицами, и добавляем три нуля (разделителя). Каждой перестановке однозначно соответствует некоторый выбор. Например, одному из вариантов покупки будет соответствовать такой код: 1101110101. Пирожные покупаются следующим образом. Количество единиц слева до первого нуля соответствует покупке эклеров, между первым и вторым нулем – покупке песочных, между вторым и третьим – покупке слоеных, единицы после третьего нуля соответствуют числу покупаемых наполеонов. В случае приведенного кода покупается 2 эклера, 3 песочных, 1 слоеное и 1 наполеон. Количество вариантов покупки пирожных равно числу перестановок из 7 объектов одного типа (единиц) и 3 объектов второго типа (нулей).
143
Если имеются предметы n разных типов (без ограничения числа предметов каждого типа) и требуется определить, сколько комбинаций можно сделать из них, чтобы в каждую комбинацию входило k предметов? Каждую комбинацию шифруем с помощью 0 и 1, причем 1 соответствуют предметам, а 0 выполняют функцию разделителей. Тогда записав k единиц и добавив (n 1) нуль, получим комбинацию, при которой выбираются k предметов первого типа и ни одного предмета остальных типов. Переставляя всеми способами эти k единиц и (n 1) нуль, мы будем каждый раз получать некоторую
расстановку, состоящую из k предметов. Тогда |
P(k, n 1) |
(k n 1)! |
||
k!(n 1)! |
|
|||
|
|
|||
14.4 Контрольные вопросы и задания |
|
|
|
|
1. Дайте определение r-выборки.
2. Перечислите основные задачи комбинаторного анализа.
Ck . n k 1
3.Перечислите основные комбинаторные конфигурации (модели комбинаторных конфигураций).
4.Приведите примеры комбинаторных конфигураций.
5.Поясните основные правила, используемы при решении комбинаторных задач.
6.Поясните правило суммы и приведите пример задачи, для решения которой используется данное правило.
7.Поясните правило произведения и приведите пример задачи, для решения которой используется данное правило.
8.Дайте определение понятия «перестановка». Приведите формулу расчета количества перестановок без повторения элементов в них.
9.Дайте определение понятия «перестановка». Приведите формулу расчета количества перестановок с повторением элементов в них.
10.Дайте определение понятия «размещение». Приведите формулу расчета количества размещений без повторения элементов в них.
11.Дайте определение понятия «сочетание». Приведите формулу расчета количества сочетаний без повторения элементов в них.
12Дайте определение понятия «размещение». Приведите формулу расчета количества размещений с повторением элементов в них.
13.Дайте определение понятия «сочетание». Приведите формулу расчета количества сочетаний с повторением элементов в них.
144

ЛЕКЦИЯ 15. ПРИНЦИП ВКЛЮЧЕНИЯ И ИСКЛЮЧЕНИЯ
15.1 Теорема и формула включений и исключений
Главная теорема комбинаторики (Теорема о включениях и исключениях). Пусть имеется множество из N объектов произвольной природы. На этом множестве пусть задано n свойств. Каждый объект может обладать либо не обладать некоторыми из этих свойств. Сами свойства обозначим: 1,2 ,...,n . Будем обозначать N (i ) – количество объектов точно
обладающих свойством i и может |
быть какими-то другими, а |
N (i , j ) – |
число объектов, не обладающих ни |
свойством i , ни свойством |
j . Тогда |
число объектов, не обладающих ни одним из перечисленных свойств:
N (1,2 ,...,n ) N N (1) N (2 ) ...
N (n ) N (1 2 ) ... N (1 n ) N (2 3 ) ...N (n 1 n ) N (1 2 3 ) ... ( 1)n N (1 2 3... i )
Пример. На предприятии работает 67 человек. Из них 48 знают английский, 35 – немецкий и 27 – оба языка. Сколько человек не знают ни английского, ни немецкого?
Результат можно получить следующим образом. Построим диаграмму, на которой изобразим прямоугольник, соответствующий общему числу работающих (67) и две пересекающиеся области A и B по 48 и 35 человек (знающих английский и немецкий языки). На диаграмме общая часть этих двух областей соответствует 27 – количеству работающих, которые знают оба языка. Требуется найти область прямоугольника, не входящую ни в область A , ни в область B .
Очевидно, что N = 67 – 48 – 35 + 27 = 11.
Пусть теперь 20 человек знают французский, 12 – английский и французский, 11 – английский и немецкий и 5 – все три языка.
145

Тогда в соответствии с теоремой количество человек, не знающих ни одного из трех перечисленных языков (но может быть знающих китайский язык), равно N = 67 – 48 – 35 – 20 + 27 + 12 + 11 – 5 = 9.
15.2 Решето Эратосфена
Выпишем все числа от 1 до N . Сколько чисел делится на k ? Очевидно,
N |
|
, где |
x обозначает целую часть числа x. Тогда, легко подсчитать |
|
k |
|
|
количество чисел, не делящихся в данном диапазоне на k1, k2, k3,...
Пример. Сколько чисел от 1до 100 не делятся на 5 и 7?
Воспользуемся теоремой о включениях и исключениях. Под первым свойством чисел будем понимать делимость на 5, под вторым – делимость на 7. На 5 делятся 20 чисел. На 7 делятся 14 чисел. На 35 делятся 2 числа. Следовательно, не делятся на 5 и 7: 100 – 20 – 14 + 2 = 68 чисел.
15.3 Частный случай теоремы о включениях и исключениях
В некоторых случаях количество объектов, обладающих определенным набором свойств, зависит только от числа этих свойств. Тогда формула для подсчета числа объектов, не обладающих ни одним из выделенных свойств, упрощается.
При произвольном n имеем:
N(n) N C1 |
N (1) C2 N (2) ... ( 1)n N(n) |
||
|
n |
|
n |
В общем случае при перестановке n предметов количество расстановок, |
|||
при которых ни один предмет не находится на своем месте: |
|||
|
|
N(n) n! 1 |
|
|
Cn (n 1)! 2 |
||
|
Cn (n 2)! ... ( 1)n 0! Dn |
||
N n |
n! C1 (n 1)! C2 |
(n 2)! ... ( 1)n 0! D . |
|
|
n |
n |
n |
Полученное |
значение |
Dn |
иногда называют формулой полного |
беспорядка или субфакториалом. Субфакториал
Dn n! 1 1!1 2!1 3!1 ...
Dn можно представить и так:
(1)n n! ,
146
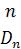
где выражение в [...] стремится к e 1 при неограниченном возрастании n .
|
|
Субфакториал имеет |
свойства, |
похожие |
на |
свойства |
обычного |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
факториала. Например, n! (n 1) |
|
(n 1)! |
(n 2)! – для обычного факториала, |
|||||||||||||||
Dn (n 1) Dn 1 |
Dn 2 |
– |
для |
|
субфакториала. |
Субфакториалы легко |
||||||||||||
вычисляются по формуле D n D |
|
(1)n . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
Некоторые начальные значения субфакториалов: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
4 |
|
|
|
5 |
|
6 |
7 |
|
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
2 |
9 |
|
|
|
44 |
|
255 |
1784 |
|
14273 |
128456 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15.3 Контрольные вопросы и задания
1.Дайте определение главной теоремы комбинаторики (Теорема о включениях и исключениях).
2.Приведите общую постановку задачи включений и исключений
3.Приведите общую формулу включений и исключений.
4. В каких задачах применяется теорема о включениях и исключениях.
5.Что представляет собой решето Эратосфена?
6.Обоснуйте частный случай теоремы о включениях и исключениях.
ЛЕКЦИЯ 16. ЗАДАЧИ О РАСПРЕДЕЛЕНИИ ПРЕДМЕТОВ ПО УРНАМ
(УРНОВЫЕ СХЕМЫ РЕШЕНИЯ КОМБИНАТОРНЫХ ЗАДАЧ)
16.1 Задачи о размещении предметов
Решая задачи размещения (распределения предметов по урнам) необходимо определить, являются ли предметы одинаковыми или различными, учитывать порядок или нет, различаются ли урны между собой.
Если невозможно однозначно что-либо определить, то необходимо сделать предположение.
16.2 Распределение n разных предметов по k урнам
147
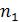
Количество размещений по k урнам n разных предметов при условии, что
в первую урну попало |
предметов, во вторую – |
n2 ,..., в последнюю – |
nk |
|||||
предметов, равно P(n1, n2 ,..., nk ) |
|
|
n! |
, n n1 n2 ... nk . |
|
|||
|
|
|
|
|
||||
n1!n2 !...nk ! |
|
|||||||
|
|
|
|
|
||||
16.3 Распределение n одинаковых предметов по k урнам |
|
|||||||
Установим, что n одинаковых предметов между k урнами можно |
||||||||
разделить P(n,k 1) Cn |
Ck 1 |
|
способами. |
|
|
|||
n k 1 |
n k 1 |
|
|
|
|
|
||
Количество искомых распределений n одинаковых предметов между |
k |
|||||||
урнами равняется количеству |
перестановок из |
(n k 1) предметов |
с |
|||||
повторениями n предметов первого типа и (k 1) предметов второго типа, т.е. равно P(n,k 1) .
Если делить справедливо, с уровнем справедливости r , то каждый участок распределения должен получать минимум r предметов. Тогда сначала раздадим каждому по r предметов. После чего остается (n kr) предметов,
которые и распределим по усмотрению. Это можно сделать Cnk kr1 k 1 Cnk k1(r 1)
способами.
16.4 Распределение разных предметов без учета порядка предметов по урнам
Нужно разделить n разных предметов по k урнам, емкость которых не ограничена. Первый предмет можно положить в любую из k урн, второй(независимо от первого), тоже в k урн и т.д. По правилу произведения предметы можно разделить k n способами.
16.5 Распределение разных предметов с учетом их порядка в урнах
Если не ограничивать количество предметов в урнах и если предметы не разнятся между собой, то количество таких распределений равно Cnk k1 1
Каждому способу разделения одинаковых предметов между урнами соответствует n! способов распределения разных предметов с учетом их
148
порядка, которые получаются с помощью перестановок предметов между собой без изменения количества предметов в урнах. По правилу умножения получаем
искомое количество распределений Ck 1 |
n! |
(n k 1)! |
An |
. |
|
||||
n k 1 |
|
(k 1)! |
n k 1 |
|
|
|
|
|
16.6 Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты
Обозначим Snk количество способов разделения n разных предметов между k одинаковыми урнами так, чтобы каждая урна была не пустой. Из каждого такого распределения можно получить k ! аналоговых распределений по разным урнам. Таким образом, количество M (n, k) распределений n разных предметов между k разными урнами с использованием каждой урны в каждом распределении (не пустых урн) равно M (n, k) k!Snk (5.15).
16.6.1 Числа Моргана
Число M (n, k) носят название чисел Моргана.
Формула S k |
1 |
k n C1 |
(k 1)n C2 |
(k 2)n ... ( 1)k 1Ck 11n |
выплывает из |
||
|
|||||||
n |
k! |
k |
k |
k |
|
|
|
|
|
|
|
||||
формулы включений и исключений.
16.6.2 Числа Стирлинга
Числа Стирлинга – комбинаторные понятия, введенные Джеймсом Стирлингом в середине XVIII века. Числа Snk называются числами Стирлинга второго рода. Числам Стирлинга Snk удовлетворяет рекурсивное соотношение
S k |
kS k S k 1. |
|
|
|
|
|
n 1 |
n |
n |
|
|
|
|
|
Число |
Стирлинга первого |
рода s(n,k) равно количеству способов |
|||
представления n объектов в виде |
k |
циклов и обозначается |
n |
(читается ― k |
||
k |
||||||
|
|
|
|
|
|
|
циклов из n ‖).
149

Например, циклы из 4 элементов a,b,c,d , b,c,d,a , c,d,a,b и d, a,b,c являются одинаковыми. Цикл можно прокручивать, так как его конец соединен с началом.
Пример. Например, существует 11 различных способов составить два цикла из четырех элементов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1,2,3 |
|
4 |
|
, 1,2,4 3 , 1,3,4 |
|
|
2 |
|
|
, |
|
2,3,4 1 , 1,3,2 |
|
|
4 |
, 1,4,2 |
3 , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||
|
1,4,3 |
|
2 |
, |
|
2,4,3 1 , 1,2 |
|
|
3,4 |
|
|
|
, |
|
1,3 2,4 |
, 1,4 |
|
|
2,3 Поэтому 4 11. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Единичный цикл (цикл, состоящий из одного элемента) – это то же самое, |
|||||||||||||||||||||||||||||||||
что |
и |
|
|
единичное |
множество. |
2-цикл |
подобен |
2-множеству, поскольку |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A, B |
|
|
|
B, A |
как и |
|
A, B |
|
|
|
B, A |
|
. Однако уже существует два различных 3- |
||||||||||||||||||||||
цикла: |
|
A, B,C |
и A,C, B . |
|
Из любого n -элементного множества могут быть |
|||||||||||||||||||||||||||||||
составлены n! |
n |
(n 1)! |
|
циклов, если |
n 0 (всего имеется n! перестановок, а |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каждый цикл соответствует сразу n из них, так как отсчет цикла может быть
начат с любого из его элементов). Поэтому n (n 1)!1
Если все циклы являются единичными или двойными, то |
n |
n |
k |
k |
|
|
|
|
n |
n |
n |
|
n |
2 |
|
|
Например, n n 1, |
n |
1 n 1 Cn |
|
|
|||
|
|
|
|
|
|
|
|
Выведем рекуррентную формулу для вычисления чисел Стирлинга |
|||||||
первого рода. |
Каждое |
представление |
n объектов в виде |
k циклов |
либо |
||
помещает последний объект в отдельный цикл s(n 1,k 1) |
способами, |
либо |
|||||
вставляет этот объект в одно из s(n 1, k) циклических представлений первых |
|||||||
n 1 объектов. |
В последнем |
случае |
существует n 1 различных способов |
||||
подобной вставки. Например, при вставке элемента d в цикл a,b,c можно
получить только 3 разных цикла: |
a,b,c,d , a,b,d,c , a,d,b,c . Таким образом, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рекуррентность имеет вид |
|
n |
|
|
|
n 1 |
(n 1) |
|
n 1 |
, n 0 |
|
|
|
|||||
k |
k 1 |
k |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
N 0n |
1n |
n2 |
|
|
3n |
|
n4 |
5n |
6n |
7n |
8n |
9n |
||||||
01
10 1
150
