
ДМ_Конспект
.pdf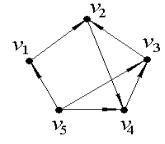
вершин, в которые дуги входят (если есть дуга, исходящая из вершины vi и входящая в vj, то элемент матрицы смежности, стоящий на пересечении i-той строки и j-того столбца равен 1, иначе – 0).
Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической).
20.4 Алгоритм выделения компонент сильной связности
1.Присваиваем p=1 (p − количество компонент связности), S1 S(D) .
2.Включаем в множество вершин Vp компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3.Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем p=p+1 и переходим к п. 2.
Пример.
Выделим компоненты связности ориентированного графа, изображенного на рис. 20.4. В данной задаче количество вершин n=5.
Рисунок 20.4
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
191
0 |
1 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
. |
|||||
A(D) |
0 1 |
0 0 |
0 |
|
||
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|||||
Найдем матрицу достижимости для данного ориентированного графа:
0 0 0 1 |
0 |
|
0 0 1 |
0 |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
|
, |
|
|
, |
|||||
sign A2 (D) |
0 |
0 |
0 |
1 |
0 |
|
sign A3 (D) |
0 |
0 |
1 |
0 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
||||
|
0 |
1 |
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
||||||||||
0 |
1 |
0 |
0 |
0 |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|||||
sign A4 (D) |
0 |
1 |
0 |
0 |
0 |
|
, |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|||||
Следовательно,
1 |
0 |
0 |
0 |
0 |
|
0 1 0 0 |
0 |
|
0 0 0 1 |
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
0 0 |
0 |
1 |
0 |
|
0 0 1 0 |
0 |
|
|||||||||
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
||||||
T (D) sign |
0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
0 |
1 |
0 |
|
0 0 |
1 |
0 |
0 |
|
0 1 0 0 |
0 |
|
|||||||||
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
||||||
|
0 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 0 1 0 |
0 |
0 1 0 0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
|||||||||||
|
0 |
1 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
. |
|||||||||||||||
|
0 |
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, матрица сильной связности будет следующей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
. |
S (D) |
0 |
1 |
1 |
1 |
0 |
|
& |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
1 |
|
|
|
||||||||||||||
Присваиваем |
p=1 |
S1 S(D) |
и |
составляем |
множество |
вершин первой |
||||||||||||||
компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины V1 v1 .
Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине v1, чтобы получить матрицу S2(D):
192

|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
S2 |
|
1 |
1 |
1 |
0 |
. |
(D) |
1 |
1 |
1 |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
||||
Присваиваем p=2. Множество |
вершин |
второй компоненты связности |
||||
составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть V2 v2 , v3, v4 . Составляем матрицу смежности для компоненты сильной связности D2 исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
0 |
0 |
1 |
|
|
|
|
|
|
. |
A(D2 ) |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
|
|||
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента: S3(D) 1 и присваиваем p=3. Таким образом, третья компонента
сильной связности исходного графа, как и первая, состоит из одной вершины
V3 v5 .
Таким образом, выделены три компоненты сильной связности
ориентированного графа D (рис. 20.5): |
|
|
D1: |
D2: |
D3: |
Рисунок 20.5
20.5 Метрические характеристики связных графов
Определение. Расстояние d (v, w) между вершинами v и w графа G –
это длина кратчайшей цепи между v и w . Если от вершины v до вершины w не ведет ни одна цепь, то d (v, w) .
В связном графе определенное таким способом расстояние удовлетворяет всем аксиомам метрики, а именно:
1.d (v, w) 0 , причем d (v, w) 0 только при v w.
2.d(v, w) d (w,v) .
193

3. d(v, w) d(w,t) d(v,t) .
Определение. Диаметром d (G) графа G называется максимальное расстояние d (v, w) в графе G .
Пример. В графе на рис. 20.6 различные вершины соединены минимальными цепями со следующими длинами:
d(1,2) d(1,4) d(1,5) d(1,6) d(2,3) d(3,4) d(3,6) d(4,5) 1;
d(1,3) d(2,4) d(2,5) d(3,5) d(4,6) d(5,6) d(2,6) 2, откуда следует, что диаметр
графа d (v, w) 2 .
1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
Рисунок 20.6 Определение. Грань (ячейка) плоского графа (в котором ребра
пересекаются только в вершинах) – это такая непустая замкнутая подобласть плоскости, что всякие две точки области можно соединить простой (Жордановой) кривой, внутренние (не концевые) точки которой лежат внутри области, не пересекаясь с ребрами графа. Другими словами, если плоскость разрезать по ребрам плоского графа, она распадется на связные части, которые называют гранями.
Определение. Границей грани считается множество ребер и вершин графа, принадлежащих грани. Всякий конечный плоский граф имеет в точности одну неограниченную грань, которая называется внешней гранью. Все остальные (ограниченные) грани называются внутренними.
Если в плоском графе нет циклов, то у него имеется только одна грань. Если же циклы есть, то граница каждой грани содержит цикл, но не обязательно является циклом.
Пример. На рис. 20.7 показан плоский граф с пятью занумерованными гранями. Граница грани с номером 3 состоит из двух циклов, а граница грани с номером 2 кроме цикла длины 5 включает еще дерево из трех ребер.
1
2
5
3 |
4 |
Рисунок 20.7
194
Множества ребер, образующие границы граней, могут быть разными для разных плоских укладок одного и того же графа.
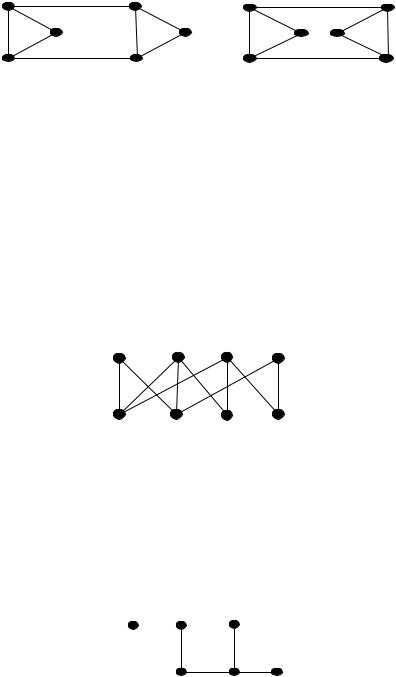
Пример. На рис. 20.8 показаны две плоские укладки одного графа. В левой укладке (рис. 20.8 а)) есть две грани, границы которых являются простыми циклами длины 5. В правой укладке (рис. 20.8 б)) таких граней нет, но есть грани, ограниченные циклами длины 4 и 6.
а) |
б) |
|
|
Рисунок 20.8 |
|
Теорема (формула Эйлера). Количество граней в любой плоской укладке |
||
планарного графа, имеющего n вершин, m ребер и k |
компонент связности, |
|
равно m n k 1. |
|
|
Определение. Эксцентриситет e(v) вершины v |
в связном графе G – |
|
это расстояние от v до наиболее удаленной от нее вершины.
Пример. Эксцентриситет вершины 8 графа на рис. 20.9 равен e(8) 3 .
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Рисунок 20.9
Определение. Наименьший из эксцентриситетов называется радиусом
r(G) графа G . |
|
|
|
|
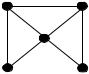
Пример. Найдем |
все |
эксцентриситеты графа на рис. 20.10: |
||
e(1) 4,e(2) 3, e(3) 2, e(4) |
3, e(5) 2, e(6) |
4 . |
||
|
1 |
2 |
3 |
|
|
|
|
|
|
5 |
4 |
6 |
Рисунок 20.10
195
Наименьший эксцентриситет равен 2, следовательно, радиус графа r(G) 2 . Наибольший эксцентриситет равен диаметру графа.
Определение. Вершина v называется центральной вершиной графа G , если на ней достигается минимум эксцентриситетов, то есть e(v) r(G) .
Вершина v называется периферийной, если e(v) d (G) .
Определение. Простая цепь, расстояние между концами которой равно d (G) , называется диаметральной цепью.
Пример. На рис. 20.11 все вершины, кроме вершины 2, являются периферийными, (1,2,3) – диаметральная цепь.
4 |
5 |
|
2 |
1 |
3 |
Рисунок 20.11 |
|
Определение. Центром графа |
G называется множество всех его |
центральных вершин; центр может состоять из единственной вершины, может – из двух и более вершин.
Пример. В графе на рис. 20.10 два центра – вершины 3 и 5.
Центр графа может совпадать с множеством всех вершин. Например, центр простой цепи при четном числе вершин n состоит ровно из двух вершин, а при нечетном – из одной; для цикла же все вершины являются центральными. Задача нахождения центральных вершин графа постоянно возникает в практической деятельности людей. Пусть, например, граф представляет сеть дорог, т.е. вершины его соответствуют отдельным населенным пунктам, а ребра
–дорогам между ними. Требуется оптимально разместить больницы, магазины.
Вподобных ситуациях критерий оптимальности часто заключается в оптимизации «наихудшего» случая, т.е. в минимизации расстояния от места обслуживания до наиболее удаленного пункта. Следовательно, местами размещения должны быть центральные вершины графа.
Реальные задачи (их называют минимаксными задачами размещения) отличаются от идеальной тем, что приходится ещѐ учитывать другие обстоятельства – фактические расстояния между отдельными пунктами, стоимость, время проезда и прочее. Для того чтобы учесть это, используют взвешенные графы.
196

20.6 Эйлеровы графы
Определение. Эйлеров цикл (эйлерова линия, замкнутая эйлерова цепь, эйлерова цепь) – это цикл, содержащий все ребра графа.
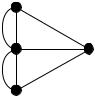
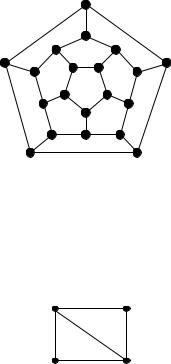
Определение. Граф, содержащий эйлеров цикл, называется эйлеровым графом (рис 20.12).
Рисунок 20.12
Определение. Если граф содержит разомкнутую цепь, содержащую все ребра этого графа, то такой граф называется полуэйлеровым (рис. 20.13).
Рисунок 20.13
Теорема 20.1. Если в связном графе все вершины четны, то этот граф содержит эйлеров цикл.
Верно и обратное утверждение: если граф содержит эйлеров цикл, то все его вершины четны.
Теорема 20.2. Если в связном графе две вершины нечетны, а все остальные – четны, то этот граф содержит эйлерову разомкнутую цепь.
Определение. Всякую линию, которую можно провести, проходя по заданным участкам точно по одному разу, называют уникурсальной.
Применительно к эйлеровым графам провести уникурсальную линию – это значит пройти по всем ребрам графа по одному разу, не отрывая карандаш от бумаги. Заметим, что разомкнутая уникурсальная линия всегда начинается с нечетной вершины и заканчивается в другой нечетной вершине. Если же начать обход полуэйлерового графа с четной вершины, то уникурсальную линию, ни замкнутую, ни разомкнутую, построить не удастся.
197
Эйлеровы графы иногда называют уникурсальными.
Теорема 20.3. Если в связном графе G содержится 2k нечетных вершин, то в нем имеется k разомкнутых эйлеровых цепей, в совокупности содержащих все ребра графа G точно по одному разу.
Используя понятие уникурсальной линии, эту теорему можно сформулировать следующим образом: если в связном графе содержится 2k нечетных вершин, то в нем имеется k разомкнутых уникурсальных линий. Чтобы изобразить такой граф, карандаш придется оторвать от бумаги не менее k 1 раз.
Пример. Граф на рис. 20.14 содержит четыре нечетные вершины, следовательно, k 2 . При его изображении карандаш от бумаги придется оторвать один раз. Если начать с вершины 1, то получим две уникурсальные линии: 1,3,4,2,1,2,4 и 2,3.
1
2
3
4 |
Рисунок 20.14
Теорема 20.4. В любом связном графе можно построить замкнутый маршрут, проходящий через каждое ребро точно два раза.
Чтобы убедиться в справедливости этой теоремы, достаточно каждое ребро графа заменить двумя параллельными ребрами и считать, что маршрут проходит по каждому ребру точно один раз. Тогда все вершины станут четными, и такой граф будет содержать эйлеров цикл.
Из этой теоремы следует, что любой граф можно изобразить, не отрывая карандаш от бумаги и проходя по каждому ребру не более двух раз.
Пример. Граф, приведенный на рисунке 6.50, можно изобразить в виде последовательности вершин так: 1,2,4,2,1,3,2,3,4, откуда следует, что два раза карандаш прошел только по ребру {2,3}.
Теорема Эйлера. Граф содержит эйлеров цикл тогда и только тогда, когда он связен и степени всех его вершин – четные.
198
20.7 Алгоритм нахождения эйлерова цикла (алгоритм Флери)
Шаг 1. Начиная с произвольной вершины n , присвоить произвольному ребру {u,v} номер 1. Затем вычеркнуть ребро {u,v} и перейти в вершину v .
Шаг 2. Пусть w – вершина, в которую перешли в результате выполнения предыдущего шага, и k – номер, присвоенный некоторому ребру на этом шаге. Выбрать любое ребро, инцидентное вершине w , причѐм мост выбирать только в том случае, когда нет других возможностей; присвоить выбранному ребру номер k 1 и вычеркнуть его.
Шаг 3. Повторять шаг 2 пока не все ребра вычеркнуты.
20.8 Гамильтоновы графы
Определение. Гамильтонов путь (или гамильтонова цепь) – путь
(цепь), содержащий каждую вершину графа ровно один раз.
Определение. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом.
Понятие гамильтонова цикла впервые появилось в связи с задачей о кругосветном путешествии, которую рассматривал сэр Уильям Гамильтон: обойти все вершины графа – названия столиц различных стран – по одному разу и вернуться в исходный пункт.
исунок 20.15 – Додекаэдр Задача нахождения гамильтонова цикла с наименьшим весом хорошо
известна как задача коммивояжера.
Определение. Гамильтонов граф – это граф, содержащий гамильтонов цикл (рис. 20.16).
Рисунок 20.16 – Гамильтонов граф
199
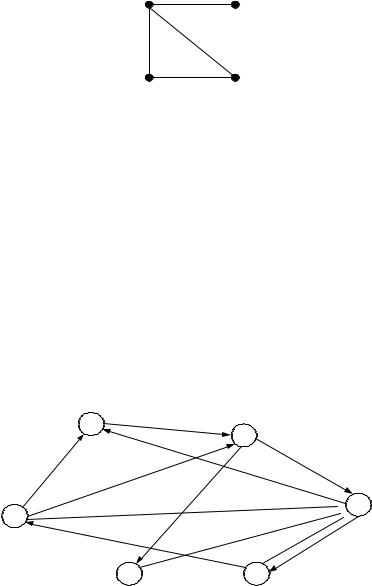
Граф, который содержит простую цепь, проходящую через каждую его вершину, называется полугамильтоновым (рис. 20.17).
Рисунок 20.17 – Полугамильтонов граф
20.9 Алгоритм Робертса-Флореса (метод перебора Робертса-Флореса)
нахождения гамильтоновых циклов в графе
Алгоритм начинается с построения матрицы (k n) |
M [mij ], где |
|
элемент mij есть i -я вершина (допустим, |
xq ), для которой в графе G ( X ,) |
|
существует дуга (xj , xq ) . Вершины xq |
можно упорядочить произвольно, |
|
образовав элементы j -го столбца матрицы M . Число строк |
k матрицы M |
|
будет равно наибольшей полустепени исхода вершины. |
|
|
a |
|
|
|
b |
|
 c f
c f 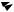
e  d
d
Рисунок 20.18 – Граф G ( X ,)
Матрица М: |
|
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
|
|
|
|
|
|
|
|
1 |
|
b |
c |
a |
c |
c |
a |
2 |
|
– |
e |
d |
f |
d |
b |
3 |
|
– |
– |
– |
– |
– |
c |
|
|
|
|
|
|
|
|
Все вершины по очереди записываем во множество S . 200
