Глава 2 Матрицы

§1 Действия с матрицами.

Произвольная совокупность действительных чисел, расположенная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей размерности (m, n). Чтобы записать матрицу, выписывают в надлежащем порядке обозначения ее элементов и получившуюся таблицу заключают в скобки или ограничивают двойными чертами. В дальнейшем матрицы будут обозначаться большими буквами. Таким образом матрицу А размерности (m, n) можно записать в виде

А = , или А =.

где а - элемент, стоящий в строке i и столбце j. Часто вместо такой подробной записи употребляют сокращенную:  a _ij  _mn .

Заметим, что вектор-строка является матрицей, состоящей из одной строки, а вектор-столбец можно рассматривать, как матрицу, состоящую из одного столбца. Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а общее число ее строк и столбцов называется порядком матрицы.

Две матрицы называются равными, если числа строк и столбцов у них соответственно равны и если равны числа, стоящие на соответственных местах этих матриц.

Основными матричными операциями являются умножение матрицы на число, сложение и перемножение двух матриц.

По определению, чтобы умножить матрицу А на число  нужно умножить на  все элементы матрицы А. Например,

7=7 = .

Суммой двух матриц А и В, имеющих соответственно равные числа строк и столбцов, называется матрица, имеющая ту же размерность и элементы, равные суммам соответствующих элементов матриц А и В. Например,

+ =.

Из этих определений непосредственно вытекают соотношения:

1. ()А = (А) ;

2. A +(B + C) = (A + B) + C;

3. A + B = B + A;

4. ( + )A = A + A;

5. (A + B) = A + B.

Введем обозначение (-1)А = -А. Для краткости вместо А + (-В) обыкновенно пишут А - В.

У м н о ж е н и е м а т р и ц. В отличие от операций сложения и умножения на число операция умножения матрицы на матрицу определяется более сложным образом. Именно пусть заданы матрицы А и В, причем число столбцов первой из них равно числу строк второй. Если А - (m, k)-матрица, В - (k, n)-матрица вида

А = , В =,

то произведением А на В называется (m, n)-матрица С = с _ij  _{m n} , элементы которой вычисляются по формуле

c_ij= a_i1 b_1j + a_i2 b_2j + . . . + a_in b_nj ( i = 1, . . . , m; j = 1, . . . , n).

Например,

= =.

Произведение двух матриц, вообще говоря, зависит от порядка сомножителей. Например,

= ,

= .

Если рассматривать матрицы не квадратные, то может случиться даже, что произведение двух матриц в одном порядке будет иметь смысл, а в обратном - нет.

Вектор можно рассматривать как матрицу, состоящую из одной строки или одного столбца. В результате умножения матрицы на вектор или вектора на матрицу получается вектор. Например,

= =,

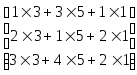[ 3, 5, 1] =

= [ 31+52+13, 33+51+14, 31+52+12] == [ 16, 18, 15].

Приведем без доказательства основные свойства умножения матриц.

6. (АВ) = (А)В; А(В) = (А)В; (АВ) = А(В).

7. (А + В)С = АС + ВС.

8. С(А + В) = СА + СВ.

9. А(ВС) = (АВ)С.

Т р а н с п о н р о в а н и е м а т р и ц. Рассмотрим произвольную матрицу

А =

размерности (m, n).

Матрица

А=

размерности (n, m), получающаяся из А заменой строк столбцами, называется транспонированной по отношению к А. В дальнейшем штрихом всегда будет обозначаться переход к транспонированной матрице.

П р и м е р. Пусть

А = .

Тогда

А=

Для любых матриц А и В имеют место следующие правила транспонирования

(А + В) =А+В

(АВ) = ВА.

Квадратная матрица А называется симметрической если

А= А,

если же

А= - А,

то матрица называется кососимметрической. Элементы, расположенные симметрично относительно главной диагонали, у симметрической матрицы равны ( а_{i j} = а_{j i} ) , а у кососимметрической противополжны (а_{i j} = - а_{j j}).

П р и м е р. Матрица

А =

является симметрической, матрица

В =

кососимметрической.