§2 Квадратные матрицы.

Выше уже отмечалось, что не любые две матрицы можно сложить или перемножить так как для осуществления таких операций необходимы известные соотношения между числами строк и столбцов. Это неудобство исчезает, если рассматривать только квадратные матрицы некоторого фиксированного порядка n. Любые две такие матрицы можно сложить или перемножить и в результате снова получится квадратная матрица того же порядка.

Особую роль среди квадратных матриц играет матрица Е, все диагональные элементы которой равны 1, а остальные - нулю, называемая единичной матрицей. Таким образом матрица Е имеет вид

Е = .

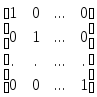Непосредственным вычислением можно показать, что для любой квадратной матрицы А имеет место равенство

АЕ = ЕА = А,

выражающее основное свойство матрицы Е. Заметим также, что для любого вектор-столбца а размеренности n ( а - вектор-строка) выполняются равенства

Еа = а,

аЕ =а .

Квадратная матрица А называется обратимой, если существует матрица Х, удовлетворяющая условию

АХ = ХА = Е.

Матрица Х, удовлетворяющая этому условию, называется матрицей, обратной к А, или обращением матрицы А. Заметим, что, если обращение матрицы существует, то оно единственно. Действительно, если существует второе обращение Y, то из равенств

X = XE= X(AY) = (XA)Y = EY = Y

следует, что X = Y.

Обращение матрицы А, если оно существует, обозначается А^{- 1}. Таким образом, по определению

АА^{- 1}= А^{- 1}А = Е.

Н а х о ж д е н и е о б р а т н о й м а т р и ц ы. Обозначим через Т() матрицу, отличающуюся от единичной только тем, что вместо единицы на i-м месте диагонали, т. е. в строке i и столбце i, стоит число . Результатом произведения матрицы Т_ii () слева на матрицу А является матрица Т_ii ()А, отличающаяся от матрицы А только строкой с номером i . В результирующей матрице элементы строки i будут иметь вид а_ij ( j = 1, . . . , n), т. е. элементы строки i матрицы А умножаются на число . Поэтому умножение матрицы Т_ii () слева на матрицу А будем называть “операцией умножения строки на число”.

П р и м е р. Пусть

А = , Т₂₂(3) = .

Тогда

Т₂₂ (3)А = =.

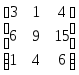Обозначим через Т_{i j} () (i  j) матрицу отличающуюся от единичной матрицы только одним элементом, стоящим в строке i и столбце j. Вместо нуля, стоящего на этом месте в единичной матрице, в матрице Т_{i j} () стоит число . Матрица Т_ij ()А будет отличаться от матрицы А только строкой с номером i . Элементы этой строки будут иметь вид а_{i k} + а_{j k} ( k = 1, . . . , n ), т. е. к элементам строки i прибавляются элементы строки j, умноженные на число . Поэтому умножение матрицы Т_ij () слева на матрицу А будем называть “операцией сложения строк”.

П р и м е р. Рассмотрим умножение матрицы А, из предыдущего примера, на матрицу Т₂₃ (2).

Т₂₃ (2)А = ==.

Предположим, что матрицу А можно привести к диагональному виду с помощью некоторой последовательности операций сложения строк и умножения строки на число. Тогда, применяя ту же последовательность операций к единичной матрице, получим обратную матрицу.

Действительно, применение данной последовательности операций к матрице А можно записать в виде произведения

Т()   Т()А.

Следовательно,

Т()   Т()А = Е,

используя свойства единичной матрицы, получим

( Т()   Т()Е )А = Е.

Последнее равенство означает, что

Т()   Т()Е = А.

Рассмотрим алгоритм нахождения обратной матрицы на примере.

П р и м е р. Пусть

А = .

Для нахождения обратной матрицы запишем расширенную матрицу, присоединив к матрице А матрицу Е

.

Операции сложения строк и умножения строки на число будем производить над расширенной матрицей, таким образом одни и те же операции будут выполняться над матрицами А и Е. В результате проведенных преобразований первый столбец должен принять вид 1, 0,0. Для этого прибавим ко второй строке первую, а из третей строки вычтем первую, умноженную на два. В результате получим

Во втором столбце на втором месте должна стоять единица. Для этого разделим вторую строку на два (или умножим на 1/2). В результате получим

.

Для обращения в ноль двух оставшихся элементов столбца вычтем из первой строки вторую, умноженную на 2, а к третьей прибавим вторую, умноженную на 3. В результате получим

.

Для того чтобы привести третий столбец к требуемому виду прибавим к первой строке третью, а из второй вычтем третью, умноженную на 2. Окончательно получим

.

Матрицу А мы привели к единичному виду. следовательно обратная матрица равна

А=.

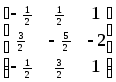П р о в е р к а.

=

= .

Строки матрицы А можно рассматривать как вектора пространства Rи применять к ним понятие линейной независимости.

Максимальное число линейно независимых вектор строк матрицы А называется рангом матрицы А или, подробнее, рангом по строкам.

Квадратную матрицу А размеренности n будем называть невырожденной если ее ранг равен n, т.е. если все строки матрицы линейно независимы.

Т е о р е м а 2.1. Матрица имеет обратную тогда и только тогда, когда она невырожденная.

Д о к а з а т е л ь с т в о. Пусть матрица А имеет обратную. Обозначим через а i-ю строку матрицы А. Тогда условие линейной зависимости

а + . . . + а = 0

строк матрицы А может быть переписано в виде

(, . . . , )А = 0.

Если матрица А обратима, то, умножая обе части равенства на А, получим (, . . . , ) = 0, т. е.  = . . . =  = 0. Следовательно вектор-строки матрицы А линейно независимы.

Обратно, пусть строки матрицы А линейно независимы. Тогда они образуют базис пространства R. Значит с помощью линейных комбинаций можно получить единичные вектора, т. е. существуют числа_{i j} (i,j=1,…,n) такие, что

 ₁₁ а ₁ + . . . +  _{1 n} а =e ₁

 _n1 а ₁ + . . . +  _{n n} а =e _n