i-808190579

111

ЛАБОРАТОРНАЯ РАБОТА № 6

КЛАССИЧЕСКАЯ ЗАДАЧА МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Цель работы – разработка оптимального плана производства с применением метода множителей Лагранжа и стандартных функций Mathcad, Matlab.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Теоретические сведения приведены в разделе 2 [1], а также в [2]. Классическая задача математического программирования формулиру-

ется в виде:

Q(x) min ,

x X

где допустимое множество

X x : x E n ,q(x) b .

Здесь E n – n-мерное евклидово пространство; q(x) – ограничения за-

дачи размерности m 1.

Размерность вектора x должна быть больше числа наложенных ограничений, т.е. n m .

ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Три предприятия выпускают продукцию. Себестоимость продукции на каждом предприятии равна

ci ai di xi ,

i 1,2,3 ,

где xi – объем выпуска продукции на i-ом предприятии; ai – доля себестоимости, не зависящая от объема выпуска продукции; di – доля себестоимости,

зависящая от объема выпуска продукции.

Определить такой план распределения выпуска продукции предприятиями, чтобы суммарная себестоимость выпуска была минимальной, т.е.

	3
Q(x) ci xi min .
	i 1					x X
При этом должны быть выполнены ограничения на суммарный объем
выпуска продукции b1 и затраты времени на производство b2
x	x	2	x			b ,
1					3	1
X t1x1 t2 x2 b2 ,
x	0, x			2	0, x 0.
1						3

1. В соответствии с условиями задачи и вариантом (таблица) записать целевую функцию и ограничения задачи.

112

											Таблица
					Исходные данные
Номер						Параметры
вариан-	a	a	a	d		d	d	t	t	b	b
та	1	2	3	1		2	3	1	2	1		2
1	10	20	30	1		2	3	1	1	10000	500
2	100	200	300	3		2	1	0	0	10000	0
3	100	20	30	10		20	40	0,5	0,5	10000	500
4	10	15	20	40		20	10	0	1	10000	200
5	10	10	10	1		1	1	0,1	0,5	10000	1000
6	20	40	100	2		1	1	1	0	10000	1000
7	100	100	10	2		2	2	0,1	0	10000	1000
8	1	2	4	10		20	10	0,1	0,2	10000	1000
9	100	1	1	15		10	10	0,1	0,1	10000	1000
10	4	2	1	4		3	2	1	0,1	10000	1000

2.Решить задачу методом множителей Лагранжа с использованием функции Find. Проверить достаточные условия существования экстремума. Если функция Find не находит решение, то необходимо щелкнуть правой кнопкой мыши на названии Find. В открывшимся контекстном меню (нелинейные) и его подменю выберите другой метод поиска (например, метод сопряженных градиентов Conjugate Gradient), либо выберите Autselect (автовыбор).

3.Решить задачу с использованием функции Minimize непосредственно по Q(x) и ограничениям задачи.

4.Решить задачу с использованием функции Лагранжа.

5.Построить графики функций Q(x) , q(x) b для x3 x3* . Перенести вручную графики q(x) b 0 на график Q(x) и определить графически оп-

тимальное решение x1* , x2* . Для построения плоского графика дважды щелк-

ните по графику и в открывшимся меню выберите подменю Quick Plot Data. Далее задайте минимальное (start) и максимальное (end) значения по обеим осям Range1 и Range2. Для нумерации линий равного уровня дважды щелкните по графику и в открывшемся окне выберите Special и поставьте галочку

впозицию Numered.

6.Решить задачу в системе Matlab с использованием функции fmincon

либо fminimax.

Выводы по работе должны включать:

1) анализ по графику выпуклости (вогнутости) Q(x) и ограничений за-

дачи;

113

2) сравнительный анализ трудоемкости методов и полученных результатов.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Почему число ограничений – равенств должно быть меньше размерности вектора x?

2.Что характеризуют множители Лагранжа λ*i ?

3.Почему множители Лагранжа называют теневой ценой ресурса?

ЛИТЕРАТУРА

1. Масальский, Г.Б. Математические основы кибернетики: учебное пособие / Г.Б. Масальский. – Красноярск: Сиб. федер. ун-т, 2014. – 215 с. (электронная версия).

2. Интрилигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1975.-608 с.

3.Макаров Е. Инженерные расчеты в Mathcad 15: Учебный курс. –

СПб.: Питер, 2011. – 400 с.: ил.

4.Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 7: Программирование, численные методы. – Спб.: БВХ-Петербург, 2005. – 752с.: ил.

114

Тестовый пример в системе Mathcad

a1 20

a2 40

a3 100 d1 2

d2 1

d3 1

t1 1

t2 0

b1 104

Поис к минимума с ис пользованием функции find

b2 103

Q(x1 x2 x3) (a1

d1 x1)

x1 (a2 d2 x2)

x2 (a3

d3 x3)

x3

q1(x1 x2 x3) b1

(x1 x2 x3)

q2(x1 x2) b2

(t1 x1

t2 x2)

L(x1 x2 x3 1 2 ) Q(x1 x2 x3) 1 q1(x1 x2 x3) 2 q2(x1 x2) - функция Лагранжа

Необходимые ус ловия экс тремума (минимума или макс имума)

x1 0

x2 0

x3 0

1 0

2 0

- начальное приближение

Given

d

L(x1 x2 x3 1 2 )

0

d

L(x1 x2 x3 1 2 )

0

d

L(x1 x2 x3 1 2 )

0

dx1

dx2

dx3

d

d

L(x1 x2 x3 1 2 )

0

L(x1 x2 x3 1 2 )

0

d 1

d 2

x Find(x1 x2 x3 1 2 )

xT 1000

4.515 103

4.485 103

9.07 103 5.05 103

L x0x1x2x3x4

4.315 107

Q x0x1x2

4.315 107

Дос таточные ус ловия с ущес твования экс тремума

Дос таточные ус ловия

d d

d d

d2

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

dx12

dx1 dx2

dx1 dx3

d2

MG

d

d

d d

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

2

dx2 dx1

dx2

dx2 dx3

d

d

d d

d2

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

L(x1 x2 x3 1 2 )

dx32

dx3 dx1

dx3 dx2

4

8.853

13

12

10

1.77 10

MG

2.346

12

12

Матрица Гес с е

10

2

3.75 10

10 12

1.725 10 12

3.175

2

x1

4

0

0

x2

G1 0

2

0

T

G1

4 x1

2

2 x2

2

2

x3

2

x3

0

0

2

115

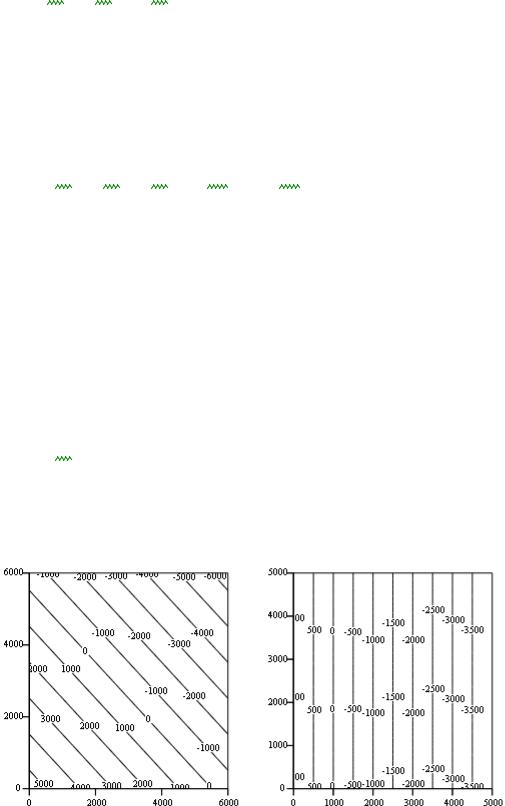
Решение задачи с ис пользованием функции minimize

Вариант 1 (непос редс твенно)

x1 5

x2 5

x3 5

- начальная точка поис ка

Given

q1(x1 x2 x3)

0

q2(x1 x2)

0

xm MinimizeQ( x1 x2 x3)

xmT

1 103

4.515

103 4.485 103

0

1

2

4.315 107

0

1

2

104

0

1

Q xm

xm xm

xm

xm xm 1

q2 xm

xm

0

Вариант 2 (с ис пользованием функции Лагранжа)

x1 0

x2 0

x3 0

1 0

2 0

- начальное приближение

Given

d

L(x1 x2 x3 1 2 )

0

d

L(x1 x2 x3 1 2 )

0

d

L(x1 x2 x3 1 2 )

0

dx1

dx2

dx3

d

d

L(x1 x2 x3 1 2 )

0

L(x1 x2 x3 1 2 )

0

d 1

d 2

x MinimizeL( x1 x2 x3 1 2 )

xT 1000 4.515 103 4.485 103

9.07 103

5.05 103

Q x0x1x2 4.315 107

L x0x1x2x3x4

4.315 107

x3 xm

Q1(x1 x2)

Q(x1 x2 x3)

q11(x1 x2)

q1(x1 x2 x3)

2

q11

q2

116

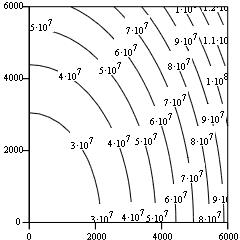
Q1

117

Тестовый пример в системе Matlab

%Тестовый пример в Matlab function lab6

clear all

X0=0:100:6000;Y0=0:100:6000;%Границы X0 и Y0 выбраны из условия ограничений, %т.е. x и y не могут принимать значения более 6000.

[Y,X]=meshgrid(Y0,X0);

s=size(X);

P=zeros(s); for i=1:s(1)

for j=1:s(2)

Z(i,j)=fun([X(i,j);Y(i,j);0]);%значения целевой функции при x3=0

end

end V=0:5000000:50000000; [C,h]=contour(Y,X,Z,V);

text_handle = clabel(C,h); grid off;hold on; x1=0:6000;x2=0:6000; xlabel('x1');ylabel('x2');

%Aeq и beq ограничения задачи q1 и q2 соответственно.

Aeq=[1 1 1;1 0 0]; beq=[10000;1000];

x0=[0;0;0];%Определим стартовую точку поиска

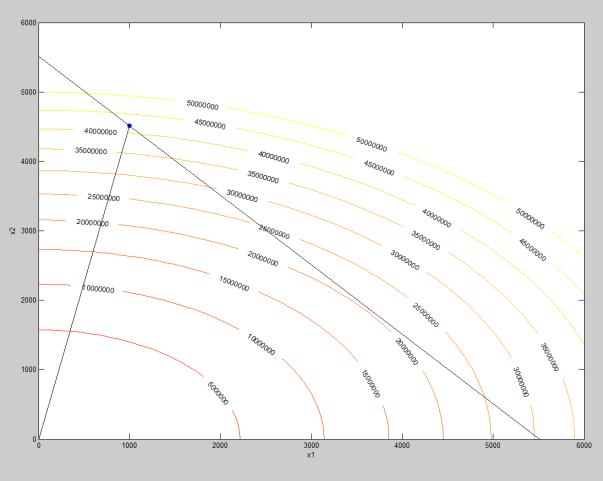
[x,Q]=fmincon(@fun,x0,[],[],Aeq,beq)

% Построение точки поиска line(x(1),x(2),'Marker','.','MarkerSize',20);

%Траектория поиска минимума plot([x0(1),x(1)],[x0(2),x(2)],'k-');

%Линия ограничений x1+x2+x3 = beq(1)

plot([x0(1),beq(1)-x0(2)-x(3)],[beq(1)-x0(1)-x(3),x0(2)],'k-'); hold off

colormap autumn

function [f]=fun(x) a=[20;40;100]; d=[2;1;1];

f=(a(1)+d(1)*x(1))*x(1)+(a(2)+d(2)*x(2))*x(2)+(a(3)+d(3)*x(3))*x(3);

>> lab6

Warning: To use the default trust-region-reflective algorithm you must supply the

gradient in the objective function and set the GradObj option to 'on'. FMINCON will

use the active-set algorithm instead. For information on applicable algorithms, see

Choosing the Algorithm in the documentation.

>In fmincon at 491 In lab6 at 25

Local minimum possible. Constraints satisfied.

118

fmincon stopped because the predicted change in the objective function

is less than the default value of the function tolerance and constraints

are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>

x=

1.0e+003 *

1.0000

4.5150

4.4850

Q =

43149550

119

ЛАБОРАТОРНАЯ РАБОТА № 7

ГРАДИЕНТНЫЙ МЕТОД ОПТИМИЗАЦИИ

Цель работы – решение задач нелинейного программирования градиентным методом и стандартными функциями Mathcad, Matlab.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Теоретические сведения приведены в разделе 3.4 [1], а также в [2÷5]. Задача нелинейного программирования (НЛП) состоит в следующем

Q(x) min ,

x X

X x : x E n ,x 0,q(x) b .

Решение задачи осуществляется рекуррентными методами вида

xk 1 xk Гk рk ,

k 0,1,...

В градиентных методах оптимизации вектор направления движения поиска

рk gradQ xk .

Реализуем простейший алгоритм градиентного метода для задач без ограничений.

Если в задаче имеются ограничения вида q(x) b и они не нарушены,

то вектор			gradQ xk ,
		рk
иначе рk grad q xk b .
Алгоритм стационарного, линейного градиентного метода оптимиза-
ции без ограничений:
1) задаем параметр γ 1,	погрешность						0 E 0.1 и матрицу парамет-
ров рабочего шага
Г		γ		1	0		γ		I
	k							k
			k	0	1
						n n

и начальную точку поиска x(0) ;

2) вычисляем k k 1 и gradQ xk ;

3) вычисляем для минимума (максимума +) новую точку поиска 4) вычисляем Q xk 1 ;xk 1 xk 1 Гk gradQ xk ;

5) проверяем условие достижения оптимума gradQ xk gradQ xk 1 E ,

если да, то переход на пункт 2, иначе останов.

120