i-808190579

ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Заданная модель:

1) полный квадратичный полином двух переменных

		Q (x) a x a x a								2	x	2	a x2 a						4		x x		2	a x2			;
		1	0		0	1	1								3		1					1		5	2
2) овраг Розенброка
		Q2 (x) 10 x2					x12 2 1 x1 2 ,											x* (1,1) .
3) центральная модель с переменным градиентом, n 3
													n
					Q3 (x) a0 a1 xi xi* 2 ;
													i 1
4)	эллиптическая модель, n 4
											n				xi xi* 2 ;
					Q4 (x) a0 ai
											i 1
5)	модели нелинейные относительно переменных xi																							и параметров ai
																a1x1
				Q5 (x) a0																		;
									exp
													a2 x2 15
																											Таблица
						Параметры модели
Номер			Коэффициенты модели																								Функция
варианта	a0	a1				a2				a3							a4							a5			Q(x)
1	2	-2.8				-2.8			-0.1								1							-1			Q (x)
																											1
2	-	-				-					-						-							-			Q (x)
																											2
3	5	-1				-					-						-							-			Q (x)
																											3
4	4	1				-1			0.2								-0.8							2			Q (x)
																											1
5	1	-3				1					-						-							-			Q (x)
																											5
6	0	1				-2				-2							-2							-			Q (x)
																											4
7	7	1				0.5			-0.1								5							-2			Q (x)
																											1
8	-	-				-					-						-							-			Q (x)
																											2
9	2	-0.5				-					-						0							0			Q (x)
																											3
10	10	1				0.5			0.1								-0.4							-2			Q (x)
																											1

121

1.Выберите из таблицы, согласно варианта, модель, полагая, xi* W ,

i1,n .

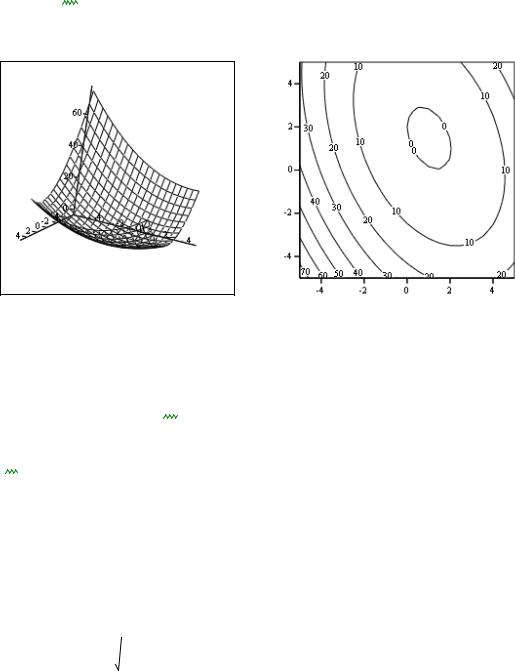
2.Проанализируйте целевую функцию Q(x) на предмет поиска ми-

нимума или максимума, используя ее график.

3. Реализуйте алгоритм градиентного метода поиска минимума (максимума) без ограничений. Решите задачи функцией Mathcad (Matlab).

4. На графике линий равного уровня проведите линейное ограничение (плоскость) вида q x1, x2 0 или q x1, x2 0 , или позиционное ограничение

x b на ваше усмотрение. Недопустимую область заштрихуйте.

5.Реализуйте алгоритм градиентного метода в условиях ограничений задачи. Решите задачу также функцией Mathcad (Matlab).

6.Выберите начальную точку в недопустимой области x0 X и решите задачу стандартной функцией Mathcad (Matlab).

Выводы по работе должны включать:

1)анализ влияния параметра γk рабочего шага на сходимость процесса поиска (график xN x* f γk ) (для Mathcad);

2)влияние параметра Е на точность решения (для Mathcad);

3)изобразите на плоскости примерные траектории движения точки xk

впроцессе поиска без ограничений и с ограничениями;

4)объясните правило останова в условиях ограничений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Поясните характерные признаки задачи НЛП.

2.Суть рекуррентных методов поиска.

3.Условие останова градиентного поиска.

4.Может ли процесс поиска расходиться и почему?

5.Противоречия в выборе матрицы Гk .

ЛИТЕРАТУРА

1.Масальский, Г.Б. Математические основы кибернетики: учебное пособие / Г.Б. Масальский. – Красноярск: Сиб. федер. ун-т, 2014. – 215 с. (электронная версия).

2.Интрилигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1975.-608 с.

3.Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. – М.: Ра-

дио и связь, 1988. – 128 с.: ил.

122

4.Макаров Е. Инженерные расчеты в Mathcad 15: Учебный курс. –

СПб.: Питер, 2011. – 400 с.: ил.

5.Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 7: программирование, численные методы. – Спб.: БВХ-Петербург, 2005. – 752с.: ил.

123

Тестовый пример в системе Mathcad

x0 1

a0 2

a1 2.8

a2 2.0

a3 0.5

a4 1

a5 0.5

Q x1 x2 a0 x0 a1 x1 a2 x2 a3 x1 x2 a4 x12 a5 x22

Q

Q

Градиентный метод поис ка минимума без функциональных ограничений

d

1

0

grad x1 x1

x2

Q x1

x2

0.05

dx1

d

0

1

grad x2 x1

x2

Q x1

x2

8

dx2

( F X k )

X0

8

E 0.05

k 0

F

Q

X

X

0 1

0

0

0

grad

x1

X

X

0

0

Grad0

grad

0

1

x2

X

X

0

0

0

1

while

Gradk

2 Gradk

2 E

0

1

k k 1

x1

grad

X

k 1

X

k 1

Gradk

grad

0

1

x2

X

X

k 1

0

k 1

1

Xk Xk 1

Gradk

F

Q

X

X

k 1

k

k 0

( F X

k )

124

k 100	Fk 0.924	Xk		1.006
				1.54
Стандартные процедуры с ис темы Mathcad
x1 8	x2 8
xx MinimizeQ x1 x2			T		Q xx0 xx1 0.926
			xx	( 1.029 1.486)

Градиентный метод поис ка минимума c функци ональными ограничениями

g x1 x2 x1

x2 4

0

gradGx1 x1 x2

d

g x1 x2

0.05

1

dx1

0

1

gradGx2 x1 x2

d

g x1 x2

dx2

( F X k )

X0

8

8

k 0

F

Q

X

X

0 1

0

0

0

while k 500

k k 1

x1

grad

X

k 1 0

X

k 1

k

grad

X

X

1

if g

X

k 1

k 1

0

Grad

x2

X

0

1

k 1 0

k 1

1

x1

gradG

X

k 1

X

k 1

0

1

otherwise

X

gradG

X

x2

k 1

0

k 1

1

Xk Xk 1

Gradk

F

Q

X

X

k 1

k

k 0

( F

X

k )

Fk 0.115 Xk

1.328

2.546

Стандартные процедуры с ис темы Mathcad

x1 8

x2 8

Given

x1 x2 4

xx MinimizeQ x1 x2

T

( 1.4 2.6)

Q xx0 xx1 0.04

xx

125

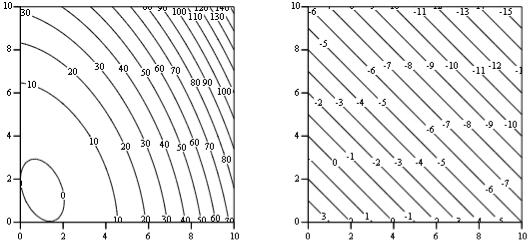
Q

g

126

Тестовый пример в системе Matlab

%Тестовый пример в Matlab

%% 1. Коэффициенты модели.

x0=1;a0=2; a1=-2.8; a2=-2.0; a3=0.5; a4=1; a5=0.5; % Q - Целевая функция

Q = @(x) a0*x0+a1*x(1)+a2*x(2)+a3*x(1)*x(2)+a4*x(1)^2+a5*x(2)^2;

%Параметры контурных линий целевой функции

X0=0:0.1:10;

Y0=0:0.1:10;

[X,Y]=meshgrid(X0,Y0);

s=size(X);

Z=zeros(s); for i=1:s(1)

for j=1:s(2) Z(i,j)=Q([X(i,j);Y(i,j)]);

end

end

%v - массив значений целевых функций для графика v=0:10:80;

%%2. Градиентный метод поиска минимума без функциональных ограничений. % x_0 - начальная точка поиска

x_0 = [8 8];

% Используем fminunc - находит минимум функции нескольких переменных.

[x_uncon, Q_uncon] = fminunc(Q, x_0) subplot(1,2,1);

% Построим контурный график целевой функции contour(X,Y,Z,v,'ShowText', 'on');

hold on

% Изобразим траеторию поиска , а именно % отметим начальную и конечную точки, соединим их прямой линией

line(x_0(1),x_0(2),'Marker','.','MarkerSize',10); line(x_uncon(1),x_uncon(2),'Marker','.','MarkerSize',20); plot([x_0(1),x_uncon(1)],[x_0(2),x_uncon(2)],'k-');

hold off

xlabel('x1'); ylabel('x2') colormap copper

%%3. Градиентный метод поиска минимума с функциональными ограничениями. % g - функциональное ограничение;

% x_0 - начальная точка поиска. g = @(x) -1*x(1) -1*x(2) + 4;

A = [-1 -1]; b = [-4];

% Используем функцию fmincon

[x_con, Q_con] = fmincon(Q, x_0, A, b) subplot(1,2,2);

% Построим контурный график целевой функции contour(X,Y,Z,v,'ShowText', 'on');

hold on

for i=1:s(1)

for j=1:s(2) Zg(i,j)=g([X(i,j);Y(i,j)]);

end

end

% v_g - массив значений функции g, контуры для которых надо отобразить v_g = 0:0.001:0.001;

contour(X,Y,Zg,v_g);

127

%Изобразим траеторию поиска минимума, а именно

%отметим начальную и конечную точки, соединим их. line(x_0(1),x_0(2),'Marker','.','MarkerSize',10); line(x_con(1),x_con(2),'Marker','.','MarkerSize',20); plot([x_0(1),x_con(1)],[x_0(2),x_con(2)],'k-');

hold off xlabel('x1');ylabel('x2') colormap copper

Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead.

> In fminunc at 365 In lab_7_1 at 23

Local minimum found.

Optimization completed because the size of the gradient is less than the default value of the function tolerance.

<stopping criteria details>

x_uncon =

1.0286 1.4857

Q_uncon =

-0.9257

Warning: The default trust-region-reflective algorithm does not solve problems with the constraints you have specified. FMINCON will use the active-set algorithm instead. For information on applicable algorithms, see Choosing the Algorithm in the

documentation.

> In fmincon at 486 In lab_7_1 at 43

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance,

and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>

Active inequalities (to within options.TolCon = 1e-006):

128

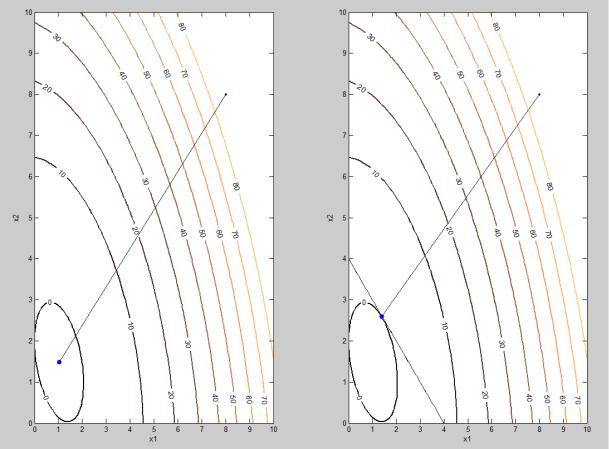
lower	upper ineqlin ineqnonlin
	1
x_con =
1.4000	2.6000

Q_con =

0.0400

129

ЛАБОРАТОРНАЯ РАБОТА № 8

ПОСЛЕДОВАТЕЛЬНЫЙ СИМПЛЕКСНЫЙ МЕТОД

Цель работы – исследование метода прямого поиска экстремума целевой функции.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Теоретические сведения приведены в разделе 3.7 [1], а также в [2]. Общая постановка задачи

					(8.1)
	Q(x) max, min			,
	x X	(kp 0)			, j ,...,m .
где X x : x E n , x x x ,i ,...,p, q		j	(x) b
i	i i			j
Алгоритм последовательного симплексного метода
Исходными данными являются: n – размерность симплекса; x0i – коор-
динаты центра исходного симплекса; x ,			x	– позиционные и функциональ-

ные q(x) b ограничения; целевая функция Q(x) ; N1 – число итераций для вписывания исходной точки х0 в ограничения задачи; r,e n – номера координат для построения графика перемещения координат вершин симплекса при поиске; – точность отыскания экстремума, kp – константа, определяющая поиск максимума (kp 1) или минимума (kp 0) (8.1).

Порядок выполнения операций следующий:

1) осуществляется расчет N , LN , параметра изменения ребра симплекса; вокруг исходной точки с координатами x0i построить симплекс,

удовлетворяющий ограничениям (8.1). Расчет координат вершин симплекса произвести по формуле

				x ji x i Lo ,
где i ,...,n – номер переменной;					j ,...,n – номер вершины симплекса;
– переменная, определяемая из выражения
,при i j ,
									,при i	j ,
					i(i )
					i
							,при i j .
		(i )

130