i-808190579

Продолжение прил. 6

71

ЛАБОРАТОРНАЯ РАБОТА № 4

ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ ДИНАМИЧЕСКОЙ МОДЕЛИ

Цель работы – преобразование и исследование динамических моделей, обработка результатов эксперимента МНК и рекуррентным МНК, анализ полученных результатов.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Динамика объекта определяется структурной схемой (рис. 4.1) и передаточными функциями ее элементов (звеньев)

W ( p)	x( p)		b pm ... b p b
			m		1	0	(4.1)
i	u( p)		a		pn ... a p 1
				n
					1

V ( p)

u( p)

Динамика

x( p)

y( p)

объекта

T

T

u kT0

y kT0

Рис. 4.1 Объект идентификации

Коэффициент усиления звена

K W (0)

b0

.

1

Экспериментальное

определение параметров

динамической модели

предполагает измерение входных и выходных переменных объекта в дискретные моменты времени t kT (см. рис. 4.1). Перейдем от непрерывной

модели (4.1) к дискретной одним из методов, рассмотренных в разделе 3.4

[1].

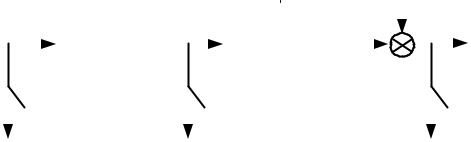
Процесс перехода к дискретной модели рассмотрим на примере объекта, представленного последовательным включением двух звеньев с параметрами (рис. 4.2)

W ( p)

x1 ( p)

K1

; W ( p)

x ( p)

K

. (4.2)

1

u( p)

T p 1

x ( p)

T p T p

1

72

V t

u t

x

(t )

y t

x (t)

p

. p

p

T

T

T

u(kT0 )

y (kT )

y (kT )

Рис. 4.2. Модель объекта

Листинг программы перехода представлен на рис. 4.3.

%Преобразование непрерывной модели

clc

clear

W1=tf(2,[3 1]);

%W1(p)

W2=tf(3,[4 1.6 1]);

%W2(p)

W=W1*W2; %ПФ разомкнутой системы

step(W) %оценка времени п.п и выбор Т0

T0=1;

W1z=c2d(W1,T0)

%переход к дискретной ПФ

W2z=c2d(W2,T0) % переход к дискретной ПФ

%Переход к непрерывной модели по результатам идентификации

% W1Z=tf(0.567,[1 -0.716],1);

%ввод оценок параметров дискретной W1

% W2Z=tf([0.364 0.288],[1 -1.408 0.619],1); %ввод оценок

дискретной W2

%W1p=d2c(W1Z);%переход к непрерывной W1

%W2p=d2c(W2Z); %переход к непрерывной W2

% Wp=W1p*W2p; % оценка ПФ системы

% step(W,'-',Wp,'--') %сравнение п.п исходной и оценки модели

Transfer function: 0.5669

----------

z - 0.7165

Sampling time (seconds): 1 Transfer function:

0.323 z + 0.2824

----------------------

z^2 - 1.469 z + 0.6703 Sampling time (seconds): 1

Рис. 4.3. Листинг программы и результаты расчета, лист 1

73

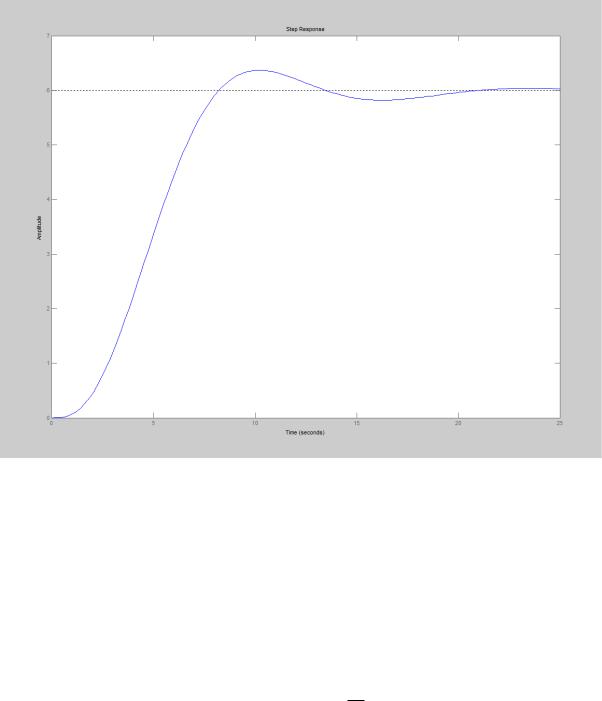
Рис. 4.3. Продолжение. Переходной процесс, лист 2

Измерению доступны u(t) , выход y (t) и выход второго звена y (t) . Съем данных осуществляется синхронно с интервалом T , выбираемого из

соотношения

T / / tnn ,

где tnn – время переходного процесса.

Для нашего примера tnn определено из графика переходного процесса

(см. рис. 4.3), tnn с, соответственно T сек.

По результатам работы программы (см. рис. 4.3) дискретная передаточная функция для первого звена

W (z)	y (z)			b				.		.
	U (z)			z а			z .
Поделим ее числитель и знаменатель на z и получим
W (z )			. z					.		(4.3)
		. z

Соответственно для второго звена

74

W2

(z)

y2

(z)

b21 z b22

0.323z 0.2824

,

y (z)

z 2

a2

z a2

2

z 2

1.469z

0.6703

1

1

поделим на z и получим

W (z )

. z . z

.

(4.4)

. z . z

Вычислим коэффициент усиления второго звена

	K	. .		. .
		. .

Как видно, сказываются ошибки округления при выводе на печать параметров дискретной передаточной функции.

Переход к разностным уравнениям. Для передаточной функции (4.3),

согласно уравнений (3.16) и (3.18) [1], имеем

	y1	(k) 0.7165y1	(k 1) 0.5669u(k 1) или	(4.5)
	y1	(k) 0.5669u(k 1) 0.7165y1 (k 1).

В общем виде разностное уравнение (4.5) имеет вид

y(k) a1 y(k 1) ... anay (k na) b1u(k nk) b2u(k nk 1) ...

... bnbu(k nk nb 1),

(4.6)

где nа=n – порядок знаменателя (4.1), nb=m – порядок числителя (4.1), nk=d+1 – транспортное запаздывание. Это линейная параметрическая модель вход-выход типа ARX (na,nb,nk) в приложении System Identification Toolbox.

Уравнение (4.5) представим в виде

				y (k) T (k) ,
где T (k) u(k 1)			y (k 1)
				– это правая часть уравнения (4.5) вектор-
1			1
строка и		.
			– это коэффициенты уравнения (4.5).
		.

Для второго звена согласно (4.4) имеем

y (k) . y (k ) . y (k ) . y (k ) . y (k ) или

y2 (k) . y (k ) . y (k ) . y (k ) . y (k ) V (k).

(4.7)

В уравнении (4.7) учтено то, что входом звена 2 является y (k) и что y (k) измеряется помехой V (k) (см. рис. 4.2).

Уравнение (4.7) запишем в векторном виде

y

(k) T

(k)

V (k) ,

(4.8)

где

T

(k) y (k )

y (k )

y

(k )

y

(k )

– вектор-строка,

T

.

.

.

. .

75

Проведение эксперимента и идентификация (оценивание) параметров динамической модели. Расчет по уравнению (4.5) возможен с момента k при определении начальных условий правой части уравнения y ( ) .

Для уравнения (4.7) расчет возможен с k и определении начальных условий y ( ) , y ( ) . Значения входных воздействий y ( ) и y ( ) для

k определены уравнением (7.5) и его начальными условиями.

Результаты эксперимента k ...N представим в векторно-матричной форме (с учетом (4.6) и (4.8)).

		y ( )			T ( )
		y ( )			T	( )
	Y			;				;
		y (k)			T (k )
					T
	y (N ) N					(N ) N

	y ( )			T ( )
Y	y (k)		;	T	(k)		.
y (N ) ( N )				T (N ) ( N )

(4.9)

(4.10)

Размерности этих матриц справедливы для системы Mathcad, где возможен индекс k . В системе Matlab, где минимальный индекс массива k все индексы указанных массивов увеличиваются на единицу.

Результаты эксперимента представим в виде

Y θ ;

Y θ

2

,

1

а неизвестные оценки параметров модели рассчитаем МНК

θ

T

Y ;

θ

T

Y .

(4.11)

T

T

1

2

Рекуррентный МНК (РМНК). Представим модели (4.6) и (4.8) соответ-

ственно в виде

(k) T (k) θ

(k ) ,

(k) T

(k) θ

2

(k ) ,

(4.12)

1

1

2

где θ1 (k ) , θ2 (k )

– оценки, полученные

на предыдущем шаге; 1 (k) ,

2 (k) – прогноз (оценка) выходных переменных звеньев на k-ом шаге поиска по результатам наблюдения T (k) и T (k) .

Тогда процедура МНК будет иметь вид [2]

θ(k) θ(k ) (k) y(k) T (k) θ(k ) ,k n,n ,...,N , (4.13)

где вектор коррекции

76

(k)	C(k ) (k)	,	(4.14)
	T (k)C(k ) (k)
а ковариационная матрица оценок параметров
C(k) C(k ) (k) T (k)C(k ) .			(4.15)

В уравнении (4.13) выражение в квадратной скобке равно невязке между измеренным на объекте значением выходной переменной y(k) и предска-

занной по модели (4.12) с оценками, полученными на предыдущем такте вы-

числений.
Исходными данными для алгоритма служат
θ( ) ; C( ) I(n m) (n m) ,	(4.16)
где число должно быть достаточно велико .

Сходимость оценок зависит от выбора исходных значений C( ) и θ( ) .

Программа исследований в системе Mathcad приведена в Приложении

4.1.

Размерность матрицы I и векторов ψ, θ – определяются из уравнений

(4.6) и (4.8).

Обратный переход к непрерывной модели. Полученные МНК оценки дискретной модели θ1 и θ2 используем для перехода к непрерывной модели. Запишем в соответствие с (4.6) и (4.8) разностные уравнения

(k) u(k 1)

y (k 1)

θ10 ,

(4.17)

1

1

θ11

θ20

(k) y (k )

y (k )

y

(k )

y

(k )

θ21

, (4.18)

2

θ22

θ23

и соответствующие им оценки дискретных передаточных функций (см.

уравнения (4.3) и (4.4))

1 (z)

θ10

;

(4.19)

− θ11

2 (z)

θ20 + θ21

.

(4.20)

2 − θ22 + θ23

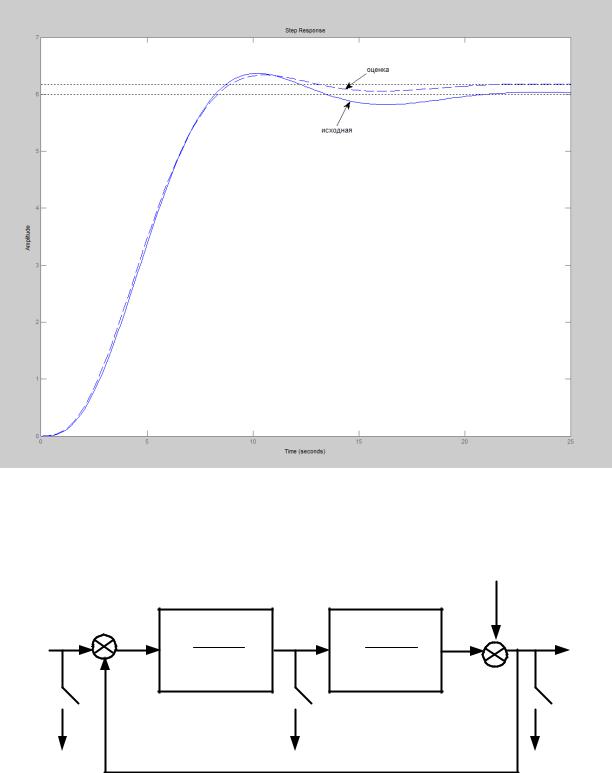
Обратный переход осуществляем в системе Matlab (см. рис. 4.3, часть 2 закомментированный блок). Сравнение графиков переходных процессов исходной и полученной по результатам эксперимента модели для уровня помехv . , представлен на рис. 4.5.

77

	Рис. 4.5. Переходной процесс исходной модели и ее оценки для σv=0.1
Идентификация параметров ss-моделей. Рассмотрим замкнутую сис-
тему примера 3.2 [1], представленную на рис. 4.6.
						V
u	e	K	x	K	x	y
	-	T p		T p
	T			T		T
u(kT0 )				y (kT )		y (kT )

Рис. 4.6. Модель объекта

Переход к моделям пространства состояний непосредственно по структурной схеме дает следующую ss-модель

78

x							T
						K
x
						T

	K							K
				x
		T							T
				x
	T

	r(t);
	(4.21)

y	x
		.
	x
Задавая параметры модели T с,			K , T с,	K , T , пе-

рейдем к дискретной ss-модели, используя процедуру с2d Matlab (рис. 4.7).

%ss-модель clc

clear

N=100; mu=0; su=1; sv=0.1; U=mu+su*randn(N,1);

%V=sv*randn(N,1); %нормально распределенная помеха с mv=0 и СКО-sv V(1:N)=0;

%U(1:N)=1; %ступенчатое воздействие для оценки tnn

T1=10; T2=5;K1=1; K2=1; T0=1; %параметры непрерывной модели A=[-1/T1 -K1/T1;K2/T2 -1/T2];

b=[K1/T1;0];

c=[1 0;0 1]; d=[0;1];

ssm=ss(A,b,c,d); %непрерывная ss-модель ssd=c2d(ssm,T0)%дискретная ss-модель

A1=[0.8961 -0.08582;0.1716 0.8103];%параметры дискретной ss-модели b1=[0.09486;0.009041];

x=zeros(2,N); %обнуление массивов y=zeros(2,N);

for k=1:N

x(:,k+1)=A1*x(:,k)+b1*U(k); %эксперимент на объекте y(:,k)=c*x(:,k)+d*V(k);

end

% plot(y(2,:)) %для оценки tnn при U(k)=1

D1=zeros(3,N); %обнуление матрицы текущих оценок параметров звена 1 (для %графика)

D2=zeros(3,N); %тоже для звена 2 alp=10^15;

C1=alp*eye(3); %ковариационная матрица оценок параметров (исходная)

C2=alp*eye(3);

Q1=zeros(3,1);%начальные оценки параметров звена 1

Q2=zeros(3,1);%тоже для звена 2

%Идентификация параметров РМНК

for k=2:N

%звено 1 ksi1=[y(1,k-1);y(2,k-1);U(k-1)];

Gk1=(C1*ksi1)/(1+(ksi1'*C1*ksi1));

C1=C1-((C1*ksi1*ksi1'*C1)/(1+(ksi1'*C1*ksi1)));

Рис. 4.7. Программа перехода к дискретной ss-модели, лист 1

79

e1(k)=y(1,k)-ksi1'*Q1;%невязка Q1=Q1+Gk1*e1(k);

D1(:,k)=Q1;% массив оценок для графика звено 2 ksi2=[y(1,k-1);y(2,k-1);U(k-1)];

Gk2=(C2*ksi2)/(1+(ksi2'*C2*ksi2)); C2=C2-((C2*ksi2*ksi2'*C2)/(1+(ksi2'*C2*ksi2))); e2(k)=y(2,k)-ksi2'*Q2;

Q2=Q2+Gk2*e2(k);

D2(:,k)=Q2;

end

disp(Q1')%печать оценок звена 1 на N-ом шаге disp(Q2')%печать оценок звена 2 на N-ом шаге subplot(211);plot(D1(1,:),'k');

grid on

title('Оценки звена 1') hold on plot(D1(2,:),'k--') hold on plot(D1(3,:),'m')

subplot(212);plot(D2(1,:),'r'); grid on

title('Оценки звена 2') hold on plot(D2(2,:),'r--') hold on plot(D2(3,:),'m')

a =
	x1	x2
x1	0.8961	-0.08582
x2	0.1716	0.8103
b =
	u1
x1	0.09486
x2	0.009041
c =

x1 x2

y1 1 0

y2 0 1 d =

u1

y1 0

y2 1

Sampling time (seconds): 1 Discrete-time state-space model.

0.8961 -0.0858 0.0949

0.1716 0.8103 0.0090

Рис. 4.7. Продолжение. Программа перехода к дискретной ss-модели, лист 2

80