i-808190579

x(N)=x(N-1); histfit(x) pause

xsr = mean(x); SX2=var(x);

x0 =x-xsr; Rxx=xcov(x,'unbiased'); [Kxx,ti]=xcov(x,'coeff'); for j=1:tm

Rx(j)=Rxx(N-1+j); rx(j)=Kxx(N-1+j); tn(j)=j;

end plot(tn-1,Rx,'--',tn-1,rx); grid on

title('Оценки Rxx,rx'); hleg1 = legend('Rxx','rx'); pause

[Px,w] = pwelch(x0,[],[],[],1); [Sx,w] = pburg(x0,1,[],1); plot(w,Px,'--',w,Sx);

grid on

title('Оценки Px ,Sx'); hleg1 = legend('Px','Sx'); pause

[Kux,ti]=xcov(U,x,'coeff');%Расчет взаимной корреляционной функции

[Rux,ti]=xcov(U,x,'unbiased'); plot(ti,Rux,'--',ti,Kux);

grid on

title('Оценка Rux,rux'); hleg1 = legend('Rux','rux'); pause

[Pux,w]=cpsd(U0,x0,[],1);%Оценка взаимного спектра plot(w,abs(Pux));

grid on

title('Оценка absPux'); pause

%Прохождение случайного процесса через нелинейное звено: for t=1:N

y(t)=(x0(t))^2;

end

%Построение графиков t=0:N-1; plot(t',[y']);

grid on xlabel('t'); ylabel('y(t)');

title('Прохождение случайного процесса через нелинейное звено)'); hleg2 = legend('y(t)=x(t)^2');

histfit(y) sptool

31

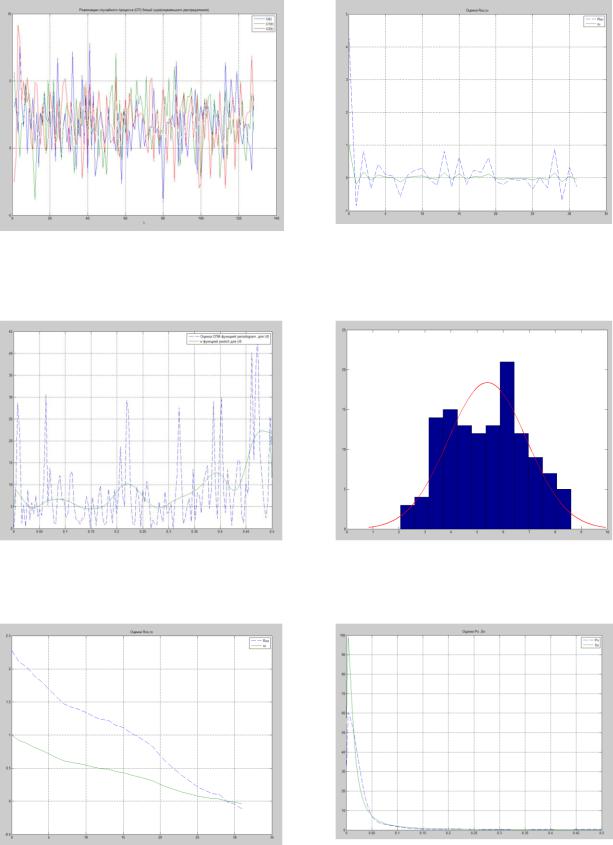
Рис. 2.1. Реализация случайного процесса U (k) типа «белый шум» и оценка его автокорреляционных функций Ruu (r) , ruu (r)

Рис. 2.2. Оценка СПМ Suu (ω) функцией	Рис. 2.3. Гистограмма случайного
periodogram и pwelch	процесса x(t)

Рис. 2.4. Оценки корреляционной функции Rxx (r) , rxx (r) и спектральной плотности мощности S xx (ω) функцией pwelch и pburg

Рис. 2.5. Оценки взаимной корреляционной функции Rux (r) , rux (r) и плотности кросс-спектра Sux (ω)

Рис. 2.6. Гистограмма временного ряда y(k) x(k)2

Рис. 2.7. Окна программы sptool

Рис. 2.8. Реализация случайного процесса x0(k) и оценка его спектральной плотности мощности

ЛАБОРАТОРНАЯ РАБОТА № 3

МЕТОДЫ РЕГРЕССИОННОГО АНАЛИЗА

Цель работы – обработка результатов пассивного эксперимента на статическом объекте методом регрессионного анализа, рекуррентным методом наименьших квадратов и стандартными средствами Mathcad и Matlab.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Теоретические сведения приведены в разделах 4.2÷4.4 и 3.4 [1]. Зависимость выходной переменной от входных переменных предста-

вим в виде

y f (x,a) V ,

(3.1)

где a – вектор неизвестных параметров (коэффициентов) модели; f ( ) – век-

тор заданных (известных) базисных функций, х – вектор входных переменных размерности n 1 1, y – наблюдаемая входная переменная, V – помеха.

Если х – скаляр, то имеем функцию одной переменной, например, полиноминальная модель второго порядка (quadratic)

y a	a x a	2	x2	V ,	(3.2)
0	1

линейную относительно неизвестных параметров а, сепарабельную модель

y a	a x a	2	sin 2x a e 0.1x V ,	(3.3)
0	1		3
также линейную относительно неизвестного вектора а.
Многомерные модели, линейные относительно вектора а, имеют вид
y a x a x ... an xn V ,				(3.4)

где x j – линеаризованные переменные (регрессоры); a j – неизвестные пара-

метры.

Как правило, первый член уравнения (3.4) представляет собой свободный член и поэтому переменную x называют фиктивной переменной.

Результаты наблюдений (эксперимента) для рассмотренных моделей представим в виде входной и выходной матриц наблюдения

x	x	x ...
x	x	x ...
X
...	...	... ...
	xN	xN ...
xN

где N – число наблюдений.

x n x n

...

xNn N n

	y
	y
	...
Y		,	(3.5)
	...
	...
yN N

35

В матричной форме результаты наблюдений
Y Xa V ,	(3.6)

где размерности матриц Y N , X N n , a (n 1) 1 , V N .

Матрица X ранга n известна (это результаты наблюдений).

Задача метода регрессионного анализа (МРА) состоит в получении оценок неизвестных параметров а и статистическом анализе полученных результатов.

Для получения оценок используют метод наименьших квадратов (МНК). В матричной форме МНК – оценки вычисляют по формуле

	^	1	X T Y ,
где M X T X	a X T X
	– матрица Фишера, симметричная квадратная матрица раз-

мерности n n ; C X T X – дисперсионная матрица размерности

n n .

Модель регрессионного анализа для линеаризованных переменных

^ ^		^	^		^
y a0	x	a1 x	... an x	n	aT x .	(3.7)
	0	1

Согласно (3.1) для исходных входных переменных и базисных функций модель регрессионного анализа имеет вид

^	^
y aT f x .		(3.8)

Методика статистического анализа и его предпосылки приведены в разделе 4.2 [1].

Рекуррентные методы оценивания.

Для моделей линейных по параметрам, выражение (3.7) на k-ом наблюдении представим моделью вида

	^	^	n ^
	y(k) aT (k 1)		x(k) a j (k 1)x j (k) , k , ,..., (3.9)
			j 0
^	–вектор оценок параметров, полученных на предыдущем (k )
где a(k 1)

шаге; x(k) x0 (k)x1 (k)...xn (k) – вектор наблюденных линеаризованных пе-

^

ременных на k-ом шаге, размерности (n 1) 1; y(k) – предсказанное значе-

ние выходной переменной.

Процедура рекуррентного метода наименьших квадратов (РМНК) обеспечивает на k-ом такте вычисление: вектора оценок коэффициентов

^

a(k) , ковариационной матрицы оценок C(k) , остаточной суммы квадратов S(k) и остаточной дисперсии Sv (k) .

36

Идентификация параметров моделей, нелинейных относительно параметров, например, вида

y			a x2	V ,
			1
	a	2	sin x a x
			3

осуществляется рекуррентными методами (нелинейный МНК и др.) (см. раз-

дел 4.4 [1]).

Стандартные функции регрессии Mathcad приведены в меню

Help→Functions→Curve Fitting and Smooth, в [2] или на сайте [4]. Рассмотрим некоторые из них.

Полиномиальная регрессия. Если зависимость (3.1) выражена полиномом n-ой степени переменной x

y a	a x a		x ... a	n	xn ,	(3.10)

то можно воспользоваться стандартной функцией регрессии a:=regress(X, Y, n)

где а – вектор оценок коэффициентов полинома, X – вектор наблюденных значений аргумента (переменной х); Y – вектор наблюденных значений функции; n – степень полинома, обычно n 4 .

Кроме того, имеются специализированные встроенные функции, когда вид модели известен априори. Причем пять из них требуют начальных условий по вектору а (исходной точки поиска):

экспонента

f (x) aebx c ,

a0:= – начальная точка a:=expfit(X, Y, a0)



y1(x):=a0·exp(a1·x)+a2

синусоида

f (x) asin(x b) c

a0:= – начальная точка a:=sinfit(X, Y, a0)



y2(x):=a0·sin(x+a1)+a2

степенная зависимость f (x) a xb c

a0:= – начальная точка a:=pwrfit(X, Y, a0)



37

	y3(x):=a0· xa1			a 2
логистическая функция
f (x) a / 1 b e cx
a0:= – начальная точка	a:=lgsfit(X, Y, a0)
	y4(x):=		a 0
		i a	1	e a2x
логарифмическая функция
f (x) a ln( x b) c
a0:= – начальная точка	a:=logfit(X, Y, a0)

y5(x):=a0·ln(x+a1)+a2

Обобщенная регрессия.

Для модели одной переменной с известным базисом fi (x) (сепарабельная модель) вида

					Q(x) a0 f0 (x) a1 f1 (x) ... an fn (x)
	f	0	(x)
	f1		(x)
Q(x):=					a:=linfit(X, Y, Q)
	fn (x)

f(x):=aT·Q(x).

Для моделей одной переменной, нелинейных относительно парамет-

ров,

f (x) a0 x a1x2 a2 sin x a3 x

применяется функция genfit. При этом, в последних версиях Mathcad, вычисление частных производных по неизвестным параметрам не требуется (см.

раздел 4.4. [1]).

Задаем

a:= – начальный вектор коэффициентов



38

	f(x, a):=	a	0	x a	1	x 2
		a 2sin(x) a3x
b:=genfit(X, Y, a, f)	F(x):=f(x, b)

Существуют различные наборы вектора оценок b, удовлетворяющие критерию минимума квадрата невязки. Поэтому не всегда процедура сходится к «истинным» коэффициентам.

Примеры совместного использования процедур регрессии и интерполяции приведены в [2].

Многомерная регрессия. Для модели (3.1) необходимо провести линеаризацию переменных и перейти к модели (3.4).

Полученные результаты эксперимента матрицы (3.5), следует подставить в процедуру regress для степени полинома n 1

a:=regress(X, Y, 1).

Матрица Х может быть и без столбца x0 1. В процедуре он формиру-

ется программно.

Параметры, выводимые функцией на печать (в виде вектора): 3 – номер функции regress в списке функций, 3 – параметр функции для других функций, n – степень полинома, 0 – признак использования матрицы Х со столбцом x0 1 (свободный член). Если без него, то этот параметр отсутствует,

параметры	(коэффициенты) уравнения регрессии в последовательности
^ ^ ^	^ ^

a1, a2 , a3 ,...,an , a0 ).

Построение 2D- и 3D-графиков для полученного уравнения регрессии (3.4) следует проводить по каждой переменной (двум переменным) при фиксированных остальных. Полученные кривые (или поверхности) отражают существенные свойства модели.

Стандартные функции регрессии в системе Matlab (R2008b).

Curve Fitting Toolbox это набор пользовательских графических интерфейсов (GUIs) и M-функций, созданных в вычислительной среде Matlab. Пакет обеспечивает первичную обработку данных, аппроксимацию, интерполяцию, МНК-сглаживание, анализ результатов, преимущественно для одномерных моделей, типовых и создаваемых пользователем (прил. 1). В версии Matlab R2012b можно обрабатывать данные функции двух переменных с построением 3D-графиков.

Вызов приложения

>> cftool

Появляется окно приложения (рис. П.1).

Активизируя кнопку Data, получим окно Data (рис. П.2), далее кнопки X Data, Y Data, вводим (импортируем) массивы X и Y из рабочей области Matlab, указывая их имена (идентификаторы). После этого, строится поле регрессии Y(x). Далее в окне Data set name зададим запоминающееся имя

39

данных и активизируем клавишу Creat data set.

В первом окне активизируем кнопку Fitting. Появляется диалоговое окно Fitting (рис. П.3), в котором следует нажать кнопку New fit, после чего все элементы управления данного окна становятся доступными.

Нажимая соответствующие кнопки, последовательно реализуем необходимые процедуры регрессионного анализа. Назначение кнопок и выбор необходимых процедур подробно представлен в прил. 1 и [4].

Описание процедур с примерами дано по ссылке Help→Product Help→Curve Fitting Toolbox→Interactive Curve Fitting→Data Fitting.

Тестовый пример приведен в прил. 3.

Обработка результатов эксперимента в пакете Statistics Toolbox [3].

Множественная линейная регрессия.

Для исходных данных вида (3.5) функция

[b,bint,r,rint,stats] = regress(Y,X)

возвращает: b – вектор оценок коэффициентов линейного по параметрам уравнения регрессии, bint – матрицу интервальных оценок параметров линейной регрессии, r - вектор остатков, rint – матрицу 95% доверительных

интервалов остатков, stats - структуру, содержащую значения статистики R2 с соответствующими ей F-статистикой и уровнем значимости p для регрессионной модели.

Размерность матрицы bint составляет n×2, где первый столбец матрицы задает нижнюю границу 95% доверительного интервала, второй – верхнюю границу 95% доверительного интервала параметра. Количество элементов вектора r равно N. Размерность матрицы rint равна N×2, где первый и второй столбцы используются для задания нижней и верхней границ 95% доверительного интервала по каждому из N наблюдений.

Статистический анализ полученных результатов осуществляет функция regstats [4].

Тестовый пример приведен в прил. 4.

Пошаговая регрессия в интерактивном режиме.

Функция

stepwise(X,Y)

позволяет получить в интерактивном режиме регрессионную модель для зависимой переменной y от независимых переменных – столбцов матрицы X (вида 3.5). Функция отображает три графических окна для управления процессом пошаговой регрессии, т.е. последовательным включением (исключением) пользователем параметра (столбца) модели.

График значений коэффициентов регрессии и их 95% доверительных интервалов приведен на (рис. 3.1). Значения коэффициентов регрессии и границ их доверительных интервалов, включенные в модель, отображаются синим цветом. Коэффициенты регрессии, исключенные из регрессионной модели, выделяются красным цветом. Включение или исключение фактора из

40