i-808190579

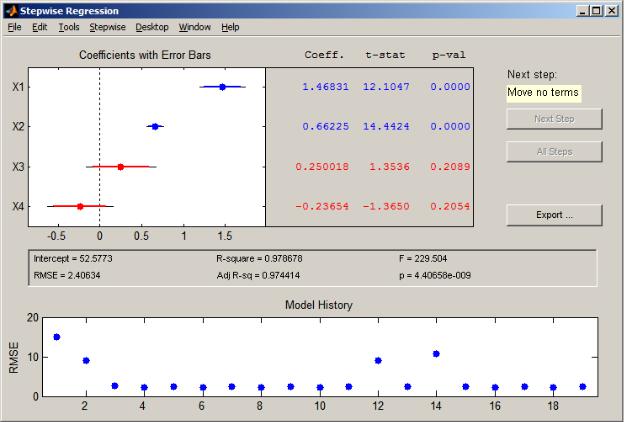
регрессионной модели выполняется щелчком левой кнопки мыши на соответствующей линии графика. Границы доверительных интервалов коэффициентов регрессии, значимо отличающихся от нуля, отображаются сплошной линией, проходящей через точку (значение коэффициента).

Коэффициенты, статистически не значимо отличающихся от нуля, расположены вдоль вертикальной штриховой нулевой линии. Значение коэффициента, не включенного в модель, рассчитывается из предположения о его включении в состав текущей регрессионной зависимости.

Исходное состояние окна: все коэффициенты не значимы (красные точки) и расположены около нулевой вертикальной линии.

Последовательно активизируя кнопку Next Step, получим пошаговое включение регрессоров в модель. Пользователь может принудительно исключить (включить) регрессор (коэффициент) из модели нажатием левой клавиши на соответствующей точке.

Нижняя часть интерфейса, модель истории, отображает среднеквадратическое отклонение (СКО) ошибки Sv модели. График

отслеживает СКО от шага к шагу, так что можно сравнивать влияние параметров на эффективность модели. Наведите курсор на синюю точку в истории, чтобы увидеть, какие условия были в модели на конкретном шаге.

Рис 3.1. Окно шаговой регрессии

41

В средней части интерфейса выводятся статистические показатели

модели: intercept – свободный член уравнения, R-square R2 – коэффициент детерминации, F – F-критерий, RMSE – среднеквадратичное отклонение ошибки Sv , Adj R-sq – скорректированный коэффициент детерминации, p –

вероятность нулевой гипотезы для свободного члена уравнения.

Меню Export используется для экспорта результатов пошаговой регрессии на текущем шаге в рабочую область Matlab.

Подробное описание функции и примеры ее применения смотри в [4]. Тестовый пример приведен в прил. 4.

Функции нелинейного регрессионного анализа.

Подробности: Help→Statistics Toolbox→Regression and Classic function→Parametric Regression→Nonlinear Model.

Нелинейная регрессия методом наименьших квадратов с использованием метода Гаусса-Ньютона

b=nlinfit(X,Y,FUN,b0),

где Y – вектор наблюдений выходной переменной, X – входная матрица (3.5), b0 – вектор начальных значений коэффициентов модели, FUN – указатель на функцию, реализующую модель. Например, FUN=@(b,x)(b(1)+b2(x)). /(b(3)·x+b(4)·power(x,2)). Значения независимых переменных определяются столбцами матрицы X.

Тестовый пример приведен в прил. 5.

Обработка данных в графическом окне [3].

Если данные представлены на графике Y=f(x) (линейная по параметрам модель), то активизируя в верхнем меню графика кнопки Tools→Basic Fitting, получим окно регрессии (рис. 3.2). В этом окне можно выбрать птичкой вид полиномиальной регрессии. Установка птички у параметра Show equations выводит в графическом окне записи уравнений регрессии (см. рис. 3.2).

Средства обработки данных из графического окна позволяют строить столбиковый или линейчатый графики погрешностей в узловых точках и наносить на эти графики норму погрешности. Норма дает статистическую оценку среднеквадратической погрешности, и чем она меньше, тем точнее аппроксимация. Для вывода графика погрешности надо установить птичку у параметра Plot residuals (График погрешностей) и в меню ниже этой опции выбрать тип графика (см. рис. 3.2).

По команде Tools→Data Statistics выводится окно с рядом статистических параметров для данных, представленных векторами X и Y . Отметив птичкой тот или иной параметр в этом окне (см. рис. 3.2), можно наблюдать соответствующие построения на графике, например, вертикалей с минимальным, средним и максимальным значениями y и горизонталей с минимальным, средним и максимальным значениями х.

42

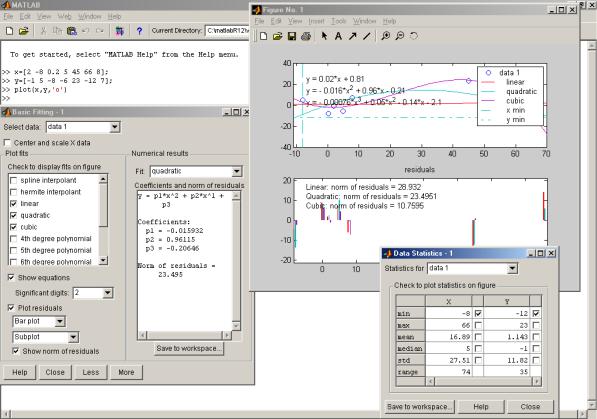
Рис.3.2. Пример обработки в окне регрессии (Basic Fitting)

Для расширения возможности окна регрессии необходимо в правом нижнем углу активизировать кнопку с жирной стрелкой →. Дополнительные окна обеспечивают анализ остатков (Residuals) , список моделей регрессии с выдачей уравнения регрессии с оценками Numerical Results и прогноз по уравнению регрессии Find Y=f(x) по заданным х.

Тестовый пример приведен в прил. 6.

ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Исходные данные:

Согласовать с преподавателем среду моделирования Mathcad или Mat-

lab.

Модель объекта идентификации имеет вид: y Q(x) V ,

где х – вектор входных переменных, размерности n; V – аддитивная помеха, распределенная по нормальному закону; Q(x) – заданная функция.

Заданная функция:

1) квадратичный полином двух переменных

Q1 (x) a0 x0 a1x1 a2 x2 a3 x12 a4 x22 ,

43

для aT 1, 1, 5,0.1,0.5 ;

2)

cепарабельная функция одного аргумента

Q (x) a x

a x a

sin x a e . x ,

для aT 2, 1,1,0.5 ; где x

– фиктивная переменная;

3)

экспонента (Exponential)

Q (x) a ea x

a

,

для aT , . , ;

4)

синусоида (Custom Equations)

для aT , , ;

Q4 (x) a0 sin x a1 a2 ,

5)

логистическая функция

Q5 (x)

a0

,

1 a e a2 х

1

для aT , , . ;

6)

степенная функция

Q (х) a хa1 a

2

,

для aT , . , ;

6

0

7)

дробно-рациональная (нелинейная по параметрам)

Q7 (х)

a0

a1x

, х 0,

a

2

x

a

3

x2

для aT , , , . ;

8)

синусоида (Sum of sin Functions)

для aT 10,0.5, π / 4 ;

Q8 (x) a0 sin(a1х a2 ) ,

9)

полиномиальная

Q (x) a x2 a

2

x a

9

1

3

для aT (0.1,2,0) .

Входные переменные представляют собой реализации случайных про-

цессов типа белый шум (Mathcad/Matlab)

х1:=rnorm(N, mu, σu), для m=W, σх=W,

х2:=runif(N,-W,W),

x=random (‘Normal’,W,W,1,N),

где N – число наблюдений; W – вариант.

Закон распределения помехи

V:=rnorm(N,0,σV)

σV =0.1W

v= random (‘Normal’,0,0.1*W,1,N).

Порядок выполнения в Mathcad:

1.

Выберите согласно варианта W модель объекта идентификации и

проведите пассивный эксперимент на модели.

44

2.Для моделей линейных по параметрам реализуйте алгоритм метода регрессионного анализа, включая статистический анализ полученных результатов согласно разд. 4.2 [1]. Проанализируйте полученные результаты.

3.Для моделей нелинейных по параметрам выберите подходящую стандартную процедуру функции регрессии Mathcad и обработайте полученные результаты наблюдений пассивного эксперимента.

4.Постройте графики исходных данных и уравнения регрессии. Сравните полученные результаты и выскажите суждения об эффективности использованных процедур.

5.Для моделей линейных по параметрам реализуйте алгоритм рекуррентного метода наименьших квадратов для обработки результатов пассивного эксперимента. Постройте графики изменения коэффициентов регрессии

^

a j f (k) . Проанализируйте полученные результаты.

6. Пункты 1÷5 выполнить при отсутствии помех (V 0). Тестовый пример приведен в прил. 2.

Порядок выполнения в Matlab:

1.Выберите, согласно варианта W модель объекта и проведите пассивный эксперимент на модели.

2.Согласно Приложения 1 определите тип параметрической модели.

3.Обработайте результаты эксперимента стандартными процедурами Matlab (m-файл) (для линейной по параметрам модели).

4.Обработайте результаты эксперимента в режиме шаговой регрессии (для линейной по параметрам модели).

5.Обработайте результаты эксперимента в режиме графического окна (для линейной по параметрам модели).

6.Обработайте результаты эксперимента в режиме cftool.

7.Пункты 1‚6 выполнить при отсутствии помех (V 0).

Тестовые примеры приведены в прил. 3‚6.

Выводы по работе должны включать:

1)объяснение процедуры формирования линеаризованных переменных для матрицы наблюдений X N n ;

2)вычисление оценок неизвестных коэффициентов методом наименьших квадратов;

3)сопоставление оценки дисперсии воспроизводимости SV с заданной

дисперсией помехи V ;

4) объяснение результатов проведенного статистического анализа для моделей, линейных по параметрам;

45

5)объяснение основных моментов стандартной функции регрессии

Mathcad (Matlab);

6)достоинства и недостатки использованных методов;

7)механизм вычисления оценок неизвестных коэффициентов рекуррентным методом наименьших квадратов;

8)сравнение полученных оценок параметров модели с заданными (истинными);

9)влияние уровня помех на точность оценок параметров модели;

10)влияние начальных условий на сходимость РМНК-оценок.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Нарисуйте структурную схему объекта идентификации.

2.Понятие пассивного эксперимента.

3.Что означает выражение «модель линейная по параметрам»? Дайте

вобщем виде запись модели линейной по параметрам.

4.Дайте общий вид матриц наблюдения входов и выхода.

5.Матричная форма записи результатов эксперимента.

6.Матричные представления МНК.

7.Предпосылки МРА.

8.Поясните выражение «модель структурно адекватна объекту».

9.Можно ли проводить статистический анализ для помех, распределенных по равномерному закону?

10.Что делать, если один из оцениваемых параметров модели оказался незначимым?

11.Как проверить работоспособность модели?

12.Что делать, если достоверность наблюдений не равнозначна?

13.Можно ли использовать рекуррентные алгоритмы в задачах идентификации нестационарных объектов?

14.Можно ли проводить статический анализ для моделей нелинейных по параметрам?

ЛИТЕРАТУРА

1.Масальский, Г.Б. Математические основы кибернетики: учебное пособие с грифом СибРО УМО вузов РФ / Г.Б. Масальский. – Красноярск:

Сиб. федер. ун-т, 2012. – 176 с.

2.Макаров Е. Инженерные расчеты в Mathcad 15: Учебный курс. –

СПб.: Питер, 2011. – 400 с.: ил.

3.Дьяконов В.П. MATLAB. Полный самоучитель. – М.: ДМК Пресс,

2012. – 768 с.: ил.

4.Образовательный математический сайт Exponenta.ru. Режим досту-

па: http://www.exponenta.ru/

46

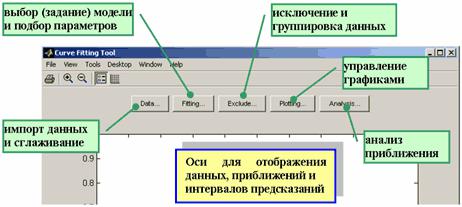
Приложение 1

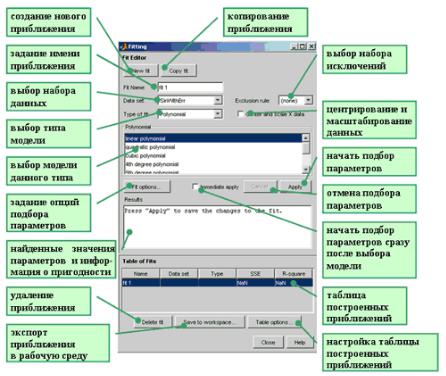
Окно Curve Fitting Toolbox [4].

Окно приложения (ниже приведена только часть окна cftool с указанием назначения основных его компонент).

Рис. П.1. – Окно приложения cftool (Matlab R2008b)

Основные этапы решения задачи о подборе параметров параметрической модели, приближающей данные, в приложении cftool таковы:

1)импорт данных (кнопка Data);

2)построение, при необходимости, правил исключения некоторых значений, или исключение вручную в таблице, или группировка данных для приближения их частей различными моделями (кнопка Exclude);

3)выбор стандартной параметрической или непараметрической модели, входящей в Curve Fitting Toolbox, или создание собственной модели, подбор параметров с предварительным указанием их границ и начальных приближений, целевой функции и методов решения, а также просмотр полученных значений и информации о пригодности полученного приближения

(кнопка Fitting);

4)анализ данных, включающий вычисление полученного приближения в заданных точках (включая экстраполяцию), его интегрирование и дифференцирование (кнопка Analysis).

После активизации Data в раскрывающихся списках X Data и Y Data следует выбрать имена переменных рабочей среды Matlab, т.е. X Data и Y Data, соответственно (рис. П.2). После этого, на правой панели окна Data строится примерный график выбранных данных.

Раскрывающийся список Weights предназначен для выбора вектора, содержащего веса. Если это не требуется, то веса можно не указывать, по умолчанию они все равны единице.

47

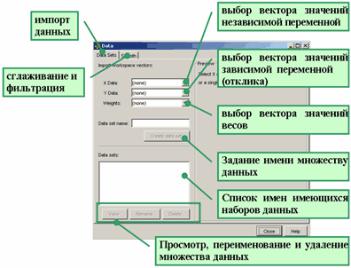
После выбора векторов с данными следует задать имя множеству данных. Для этого следует ввести его имя, например, Lab 3 в строку ввода Data set name и нажать кнопку Create data set.

Рис. П.2 – Ввод данных

Множество данных создано, его график отобразился на осях основного окна приложения cftool. В окне Data можно также осуществлять сглаживание данных (вкладка Smooth), выбирая различные способы сглаживания (см. рис.

П.2).

Для перехода к диалоговому окну, предназначенному для выбора модели и подбора параметров, следует нажать кнопку Fitting в основном окне приложения cftool. Появляется окно регрессии (рис. П.3). После активизации кнопки New fit становятся доступными элементы окна.

Рассмотрим параметрическую модель, которая является синусом или суммой синусов. В раскрывающемся списке Type of fit выберем Sum of Sin Functions. Список, расположенный в нижнем окне, сменит название, теперь он называется Sum of Sin Functions и содержит восемь функций, каждая из которых является линейной комбинацией синусов, причем параметры входят как линейно a1,a2 ,...,a8 , так и нелинейно b1,b2 ,...,b8 и c1,c2 ,...,c8 :

a1 sin b1x c1 ,

a1 sin b1x c1 a2 sin b2 x c2 ,

a1 sin b1x c1 a2 sin b2 x c2 ... a8 sin b8 x c8 .

Выберем в списке первую модель a1 sin b1x c1 и нажмем кнопку

Apply. После вычисления коэффициентов приближения в окно Results выводится следующая информация:

Тип модели:

General model Sin1:

48

f(x) = a1*sin(b1*x+c1).

Рис. П.3 – Окно регрессии (Fitting)

Найденные значения коэффициентов вместе с доверительными интервалами, соответствующими уровню вероятности 95%:

Coefficients (with 95% confidence bounds): a1 = 7.019 (6.966, 7.072)

b1 = 1 (0.995, 1.006)

c1 = 6.275 (6.261, 6.289).

Вычисленные критерии пригодности приближения:

Goodness of fit:

SSE: 0.1224

R-square: 0.9998 Adjusted R-square: 0.9997

RMSE: 0.08245.

Найденные значения параметров модели a1 sin b1x c1 таковы

a1 = 7.019, b1 = 1, c1 = 6.275.

Стандартные параметрические и непараметрические модели

Curve Fitting Toolbox содержит ряд стандартных параметрических и непараметрических моделей, которые выбираются в диалоговом окне Fitting.

Более подробно по ссылке Help→Curve Fitting Toolbox→Linear and Nonlinear Regression→Examples and How To→…

Рассмотрим некоторые стандартные типовые модели для параметрического и непараметрического приближения.

49

Параметрические модели.
Экспоненциальные модели (Exponential)
y aebx	f=fit(X,Y,’exp1’);		plot(f,X,Y);
y aebx cedx	f=fit(X,Y,’exp2’).
Отрезки ряда Фурье (Fourier)
		n
	y a0	ai cos(nωx) bi sin(nωx) ,
		i 1
где 1 n 8, n – Number of terms.
Сумма синусов (Sum of Sin Functions)
n
y ai sin bi x ci ,		f=fit(X,Y,’sin2’) для n=2		plot(f,X,Y),
i 1
где 1 n 8,
Степенные модели (Power)
y axb	f=fit(X,Y,’power1’); Number of terms: 1.
y axb с	f=fit(X,Y,’power2’);		plot(f,X,Y)
Полиномиальные модели (Polynomials)
n 1
y pi xn 1 i ,		f=fit(X,Y,’poly2’);		plot(f,X,Y),

i 1

где 1 n 9 .

Квадратичные полиномы второго порядка для версии Matlab R2012b.

f(x) a0 x0 a1x1 a2 x2 a11x12 a12 x1x2 a22 x22

вMatlab определы как функции переменных х, у.

‘poly22’→z=p00+p10·x+p01·y+p20·x^2+p11·x·y+p02y^2,

где коэффициенты pij определяют структуру полинома. Так,

‘poly21’→z=p00+p10·x+p01·y+p20·x^2+p11·x·y.

Обращение к функции

f=fit(х[x,y]z,’poly21’).

Дробно-рациональные модели (Rational).

Эти модели представляются дробью, в числителе и знаменателе которой стоят полиномы до пятой степени включительно. Коэффициент при старшей степени в знаменателе равен единице для однозначного определения дробно-рационального выражения.

		n 1
		pk xn 1 k
	y	k 1	,
		m
		xm qk xn k
		k 1

где 0 n 5 , 1 m 5.

50