i-808190579

14.Можно ли проверить статистическую гипотезу для параметров равномерного распределения?

15.Противоречия статистических выводов.

ЛИТЕРАТУРА

1.Масальский, Г.Б. Математические основы кибернетики: учебное пособие с грифом СибРО УМО вузов РФ / Г.Б. Масальский. – Красноярск:

Сиб. федер. ун-т, 2012. – 176 с.

2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учебное пособие. М.: Высшая школа,

1998.-400 с.

3.Рубан А.И. Теория вероятностей и математическая статистика. Учебное пособие: В 2 ч. - КГТУ. Красноярск, 1996.Ч.1.-128 с.

4.MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты

всреде Windows 95. Издание 2-е, стереотипное – М. Информационноиздательский дом «Филинъ», 1997 – 712 с.

5.Дьяконов В.П. MATLAB. Полный самоучитель. – М.: ДМК Пресс,

2012. – 768 с.: ил.

11

Тестовый пример в системе Mathcad

1. Нормальное рас пределение вероятнос тей с лучайной величины (СВ)

W 10

m W

0.5 W 5 p 0.8

x m 3 m 3

F(x) pnorm(x m )

f(x) dnorm(x m )

c qnorm(p m ) 14.208

1

a W 1

b W 1

0.8

pab pnorm(b m )

pnorm(a m )

F(x) 0

.6

pab 0.159

f(x) 0

.4

0

.2

0

10

0

10

20

30

x

2. Генерация выборок нормально-рас пределенной СВ

Nu 10

Nx 50

u rnorm(Nu m )

x rnorm(Nx m )

u1 rnorm(Nu m )

Оценка математичес кого ожидания (выборочное с реднее)

Nu 1

Nx 1

mu

1

ui

mu 9.626

mx

1

xi

mx 9.758

Nu

Nx

i 0

i

0

mu mean(u) 9.626

Оценка дис перс ии (выбо рочная дис перс ия)

Su2 var(u) 25.883

Su2 Var(u)

28.758

Sx2 Var(x) 22.836

Nu 1

Su2

1

ui mu

2

Su2 28.758

Sx stdev (x) 4.731

Nu 1

i 0

Su

Su2

5.363

Su Stdev(u) 5.363

Sx

Sx2

4.779

Оценка ковариации

cov cvar (u u1) 2.83

r corr(u u1)

0.127

r1 corr(u1 u) 0.127

3. Рас чет доверительных интервалов

Математичес кое ожидание

q 0.05

- уровень значимос ти

Найдем рас пределение Стьюдента

tq qt 1

q

Nx 1

2.01

2

	Sx					Sx
mxmin mx tq				8.4	mxmax mx tq					11.116
		Nx					Nx

Интервал для дис перс ии

12

Интервал для дис перс и и
2	q		1 1		q	Nx 1
2					2
1 0.975			2 0.025
Для рас пределенийнайдем значения для
1 qchisq ( 1 ) 70.222							2		qchisq ( 2 ) 31.555
Sxmin Sx2			(Nx 1)		Sxmax Sx2		(Nx 1)
			1				2
Sxmin 15.935					Sxmax 35.461

4.Проверка гипотез

4.1. Необходимо с равнить значение mx с заданным значением W

H0

:

mx

W

- ос новная гипотеза

H1

:

mx W

- конкурирующая гипоте за

v Nx 1 49

mx W

tNx

Nx tNx 0.358

Sx

Найдем рас пределение Стьюдента

tkr qt

1

q

v

2.01

2

tkp

Так как

N

x

- нулевую гипотезу не отвергаем

4.2. Необходимо проверить

H0

:

mu

mx

H1

:

mu mx

v Nu Nx 2

mu mx

tNx

Nu Nx v

tNx 0.079

Nu Nx

(Nu

1)

Su2 (Nx 1) Sx2

tkp qt(1 q v) 1.672

tkp

Так как

N

x

- нулевую гипотезу не отвергаем

4.3. Необходимо проверить

H0

:

Su

Sx

H1

:

Su Sx

v1 Nu 1

v2 Nx 1

- с тепени с вободы

13

v1 Nu 1					v2 Nx 1	- с тепени с вободы
F		Su2			F 1.259	- F-критерий (дис перс ио нное отношение)
n		Sx2			n
Найдем рас пределения Фишера
Fkr qF 1				q	v1 v2 2.387
				2
т. к.		Fn Fkp			нет ос нований отвергать нулевую гипотезу

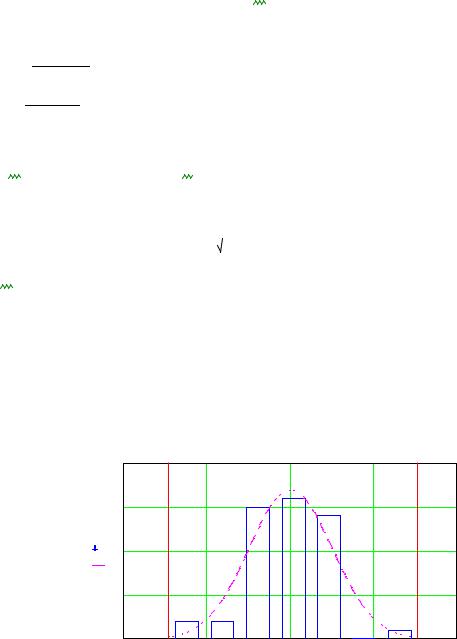
5. Пос троение эмпиричес кой функции плотнос ти рас пределения вероятнос тей и проверка гипотезы о нормальном рас пределении генеральной с овокупнос ти по критерию Пирс она

(с м. раздел 2.5. в [1]):

k 1 3.2 log(Nx)

xm in min(x)

dx xm a x xm in

k

f hist(int x) Nx

int int 0.5 dx

k 6.437	k ceil(k)	k 7
xm a x max(x)	xm in 4.504	xm a x 25.241
dx 4.249	i 0 k	int xm in dx i
		i

-рас чет чис ла наблюдений, попавших в квант

- центры интервалов ква нтования

F(r) dx dnorm(r m )

r m 3 m 3 0.1 m 3

j 0 k 1

tj		intj mx
		Sx
k 3
		k 1	f	i	Nx nT 2
2на бл					i
					nTi
		i 0

2на бл 9.325

tj 2

1

Nx dx

e 2

nT

j

j

j

2

Sx

0.05

2кр ит qchisq (1 )

2кр ит 9.488

Пос кольку 2на бл 2кр ит, то нет ос нований отвер гать гипотезу о нормальнос ти рас пределения генеральной с овокуанос ти

xm in

xm a x

0.3

f

F(r) 0.2

0.1

0
10	0	10	20	30

int r

График эмпирической функции плотности распределения вероятностей

14

% Номер варианта % Мат. ожидание распределения

% СКО распределения % Заданная вероятность

% Диапазон 3*sigma

% Интегральная функция % распределения

% Дифференциальная функция % распределения

% Находим c такое, % что P{X < c} = p

% Находим вероятность % попадания случайной

% величины в интервал [a; b]

Тестовый пример в системе Matlab

%% 1. Нормальное распределение вероятностей случайной величины (СВ) clc

W = 10; m = W;

sigma = 0.5 * W; p = 0.8;

x = m - 3 * sigma : m + 3 * sigma; F_x = normcdf(x, m, sigma);

f_x = normpdf(x, m, sigma); c = norminv(p, m, sigma);

a = W - 1; b = W + 1;

pab = normcdf(b, m, sigma) - ...

normcdf(a, m, sigma); figure(1);

plot(x,F_x,'-r');hold on; plot(x,f_x,'-b');hold off; grid on; xlabel('x');

ylabel('F(x),f(x)'); legend('F(x)','f(x)');

%%Ввод параметров выборок NU = 10; % обьем выборки U NX = 50; % обьем выборки Х mU = W;

mX = W;

sigmaU = 0.5*W; sigmaX = 0.5*W;

%--------------------------------------------------------------------------%

% Методы получения выборки

%%2. Генерация нормально распределенных выборок

U	=	random('Normal', mU , sigmaU, 1, NU);		% Генерирует матрицы размерно-
стью		1хNU и 1хNX	элементы которых
X	=	random('Normal', mX , sigmaX, 1, NX);		% распределены по нормальному
закону с математическим ожиданием mu, mx
for		i=1:NU
		U1(i)=normrnd(mU,sigmaU);
end
[xs In]=sort(X);			%сортирует в порядке возрастания и соответствующие им ин-
дексы
%%	Находим среднее значение оценки, дисперсии и ско (стандартные)
mU	=	mean(U);	% среднее значение выборки U
mX	=	mean(X);	% среднее значение выборки X
SU2 = var(U);			% оценка дисперсии выборки U
SX2 = var(X);			% оценка дисперсии выборки X
SU	=	std(U);	%СКО выборки U
SX	=	std(X);	%СКО выборки X
Cov = cov(U,U1);			% Матрица ковариации
r = corrcoef(U,U1); %Матрицы корреляции
r1	=	corrcoef(U1,U);
%--------------------------------------------------------------------------				%
%%	Вывод результатов в командное окно
str1		= sprintf(' Среднее значение выборки U = %0.2f,\r Среднее значение вы-
борки X = %0.2f,\r',mU,mX);
disp(str1);

15

str2 = sprintf(' Дисперсия выборки U = %0.2f,\r Дисперсия выборки X =

%0.2f,\r',SU2,SX2); disp(str2);

str3 = sprintf(' СКО выборки U = %0.2f,\r СКО выборки X = %0.2f\r',SU,SX); disp(str3);

str4 = sprintf(' Матрица ковариации = '); disp(str4);

disp(Cov);

str5 = sprintf(' Матрица корреляции U и U1 = '); disp(str5);

disp(r);

str6 = sprintf(' Матрица корреляции U1 и U = '); disp(str6);

disp(r1);

%% расчет квантилей

alpha = 0.05; % уровень значимости

chi2X1 = chi2inv(alpha/2,NX-1); % Хи-квадрат для выборки Х для alpha chi2X2 = chi2inv(1-alpha/2,NX-1); % Хи-квадрат для выборки Х для 1-alpha

%% 3.	Расчет доверительных интервалов
[mx,sx,MX,Sx] =		normfit(X, alpha/2); %mx-среднее, sx-СКО,MX-интервал для
mx,SX-интервал		для sx
mXMin	= MX(1);	% доверительный интервал
mXMax	= MX(2);	% мат. ожидания СВ Х
SXMin	= Sx(1);	% доверительный интервал
SXMax	= Sx(2);	% СКО СВ Х

%% Вывод результатов в командное окно

str8 = sprintf('Доверительный интервал математического ожидания СВ X: %0.2f < mХ < %0.2f\r',mXMin,mXMax);

str10 = sprintf('Доверительный интервал СКО СВ X: %0.2f < SX2 <

%0.2f\r',SXMin,SXMax); disp(str8);disp(str10);

%% 4. Проверка гипотез

%4.1 Необходимо сравнить значение mX с заданым значением W

%Гипотеза Н0: mX = W

%H1: mX ~= W

tNx1 = (NX^0.5)*abs(mX - W)/SX;

tkpX = tinv(1-alpha/2,NX-1); %Значение к-та Стьюдента для выборки X

%4.2

%Гипотеза Н0: mU = mX

%H1: mU ~= mX

tNx2 = (abs(mU - mX)/((NU-1)*SU2+(NX-1)*SX2)^0.5)*((NU*NX*(NU+NX-

2))/(NU+NX))^0.5; % Гипотеза H0: mu=mx
tkpU = tinv(1-alpha/2,NU-1);	% Значение к-та Стьюдента для выборки
U

%4.3

%Гипотеза Н0: SU = SX

%H1: SU ~= SX

Nv=[NU NX];

[cd N]=sort([SU2 SX2]);

F_n = cd(2)/cd(1); % Гипотеза H0: Su=Sx

Fkrit = finv(1-alpha/2,Nv(N(2))-1,Nv(N(1))-1); % Значение к-та Фишера

%% Вывод результатов в командное окно
str11 = sprintf('tнабл. 1 = %0.4f, tкрит.	1	= %0.4f\r',tNx1,tkpX);
disp(str11);
str12 = sprintf('tнабл. 2 = %0.4f, tкрит.	2	= %0.4f\r',tNx2,tkpU);
disp(str12);
str13 = sprintf('Fнабл. = %0.4f, Fкрит. =	%0.4f\r',F_n,Fkrit);
disp(str13);
16

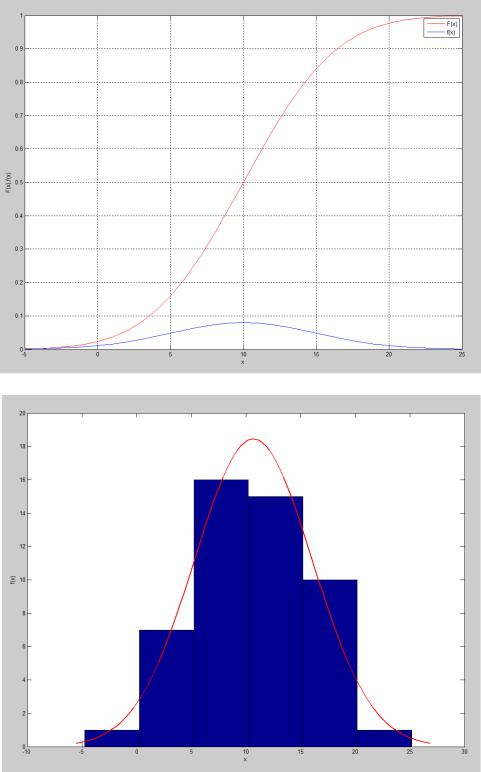
%% 5. Построение эмпирической функции плотности распределения вероятности

%и проверка гипотезы о нормальном распределении генеральной совокупности

%по критерию Пирсона.

k	=	1+3.2*log10(NX);	% количество интервалов
k	=	round(k);
	%%	вычисление теоретических частот

chi2_nabl = chi2gof(NX,'nbins',k); % хи^2 наблюдаемое. Если равно 0 значит

	% принимаем гипотезу,
	% если равно единице, то отклоняем.
dx = (max(X)-min(X))/k;	% шаг между интервалами
i=0:k;
int = min(X)+dx*i;	% начала интервалов
hint = int+0.5*dx;	% центры интервалов
hint(end) = [];
figure(2);
histfit(X,k);
xlabel('x');
ylabel('f(x)');

Среднее значение выборки U = 13.12, Среднее значение выборки X = 10.69,

Дисперсия выборки U = 78.31, Дисперсия выборки X = 29.06,

СКО выборки U = 8.85, СКО выборки X = 5.39

Матрица ковариации =

78.3123 5.1605

5.1605 39.8858

Матрица корреляции U и U1 =

1.0000 0.0923

0.0923 1.0000

Матрица корреляции U1 и U =

1.0000 0.0923

0.0923 1.0000

Доверительный интервал математического ожидания СВ X: 8.92 < mХ <

12.45

Доверительный интервал СКО СВ X: 4.39 < SX2 < 6.94

tнабл. 1 = 0.9004, tкрит. 1 = 2.0096

17

tнабл. 2 = 1.1603, tкрит. 2 = 2.2622

Fнабл. = 2.6951, Fкрит. = 2.3866

18

ЛАБОРАТОРНАЯ РАБОТА № 2

СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Цель работы – анализ дискретных случайных процессов, прохождение случайных дискретных процессов через линейные и нелинейные системы, расчет основных статистических характеристик.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ

Теоретические сведения приведены в разделах 1.5÷1.9, 2.8÷2.10 [1]. Формирование дискретного случайного процесса с заданными характе-

ристиками достигается прохождением дискретного белого шума с нормальным законом распределения через дискретное динамическое звено (дискретный фильтр) с заданной передаточной функцией W (z) .

Для моделирования дискретного белого шума в Mathcad и Matlab используют генераторы случайных чисел, рассмотренные в лабораторной работе № 1, либо генераторы шумов в специализированных приложениях. Так в приложении Signal Processing Extension Pack Mathcad генератор шума рав-

номерного распределения в интервале 0.5 0.5 с mu 0 , σu2 1/12: u:=whiten(N),

и генератор нормального белого шума mx 0 σ2x 1

u:=gaussn(N),

генерируют вектор размерности N 1.

Более подробную информацию о данных и других генераторах шумов и сигналов можно получить в справочной системе Mathcad по ссылке Справ-

ка (Help) → Электронные книги → Signal Processing → here → Signals and Classification of Signals → Noise Generators.

В приложении Matlab Signal Processing Toolbox представлены различные волнообразные сигналы (Wave form Generation).

Для получения подробной информации следует обратиться к встроенной справке или HTML-документации.

Для получения встроенной справки о конкретной функции необходимо ввести команду

>>help имя_функции. HTML-документация доступна из меню Help или по команде

>>help desk.

Дискретный случайный процесс.

Дискретный низкочастотный фильтр с дискретной передаточной функ-

цией

W (z)	b z 1
	1	,	(2.1)
	1 a z 1
	1
	19

T

, b

K (1 a ) ,

T – интервал квантования (sample time).

где a exp

0

1

T

1

1

0

Передаточной функцией (2.1) соответствует разностное уравнение ре-

курсивного фильтра

x(k) b1u(k 1) a1x(k 1),

(2.2)

либо

x(k 1) b1u(k) a1x(k) .

(2.3)

Полученные данные называют дискретным временным рядом или про-

сто временным рядом x(k) .

Свойства дискретного процесса

X (k)

определены следующими соот-

ношениями:

M X 2 (k) σ2

σ

2

b2

1 2q

;

x

u

1 1 a2

1

M X (k) U (k) σ2

b1

q;

(2.4)

u

a1

M U 2 (k) σ2

,

u

где q a1r ρ(r) , σu2ρ(r) M U (k) U (k r) .

r 1

Оценка математического ожидания, дисперсии временного ряда осу-

ществляется в соответствие с формулами раздела 2.8 [1].

Оценка корреляционной функции

^

N r

K xx (r)

x(k) x(k r), r , ,...,m .

(2.5)

N

r

k

где r – номер шага,

m – максимальное число шагов («максимальное запаз-

дывание»).

При выборе m желательно чтобы оно превысило время корреляции наблюдаемого стационарного случайного процесса. На практике для получения полезной оценки автокорреляционной функции необходимо, чтобы число наблюдений N , а число m N / . При «подозрении» на присутствие в наблюдаемом случайном процессе низкочастотной гармонической составляющей m следует увеличить до N / 2 .

В приложении Signal Processing (Mathcad) для оценки K xx (r) исполь-

зуется функция

correl(x,x)r= xk x k r ,

k

1

которая отличается от (2.5) отсутствием множителя N r .

Обращение к функции

20