gos / шпоры / ТУ

1. Уравнения динамики и статики объектов управления.

Различные по физической природе объекты управления могут описываться однотипными математическими зависимостями. Построение любой системы управления начинается с изучения объекта управления и составления его математического описания, которое может быть получено экспериментальным, аналитическим или комбинированным путем.

{В первом случае уравнения объекта получают путем постановки специальных экспериментов на объекте (метод активного эксперимента) либо статистической обработкой результатов длительной регистрации координат объекта в условиях его нормальной эксплуатации (метод пассивного эксперимента).

При аналитическом описании уравнения объекта получают на основании физико-химических закономерностей протекающих в нем процессов.

Комбинированный путь получения математического описания объектов подразумевает обычно составление уравнений аналитическим путем с последующим уточнением коэффициентов этих уравнений экспериментальным методом.} Уравнения объектов автоматического регулирования в зависимости от описываемого ими

режима работы подразделяются на уравнения статики и динамики.

Уравнения динамики описывают неустановившийся или переходный режим в объекте. Выходная координата объекта при этом является функцией времени и в общем виде уравнение динамики будет дифференциальным уравнением, содержащим производные по времени.

Объекты управления называются линейными, если они подчиняются принципу суперпозиции, который заключается в том, что реакция объекта на сумму входных сигналов равна сумме реакций на каждый из сигналов в отдельности. Линейные объекты описываются линейными дифференциальными уравнениями, то есть уравнениями, в которых искомая функция и ее производные содержатся в первой степени.

Уравнение динамики (представляет из себя ОДУ): an*(dnx(t)/dtn)+…+ a1*(dx(t)/dt)+ a0*x(t)= b0*g(t)+…+ bm*(dmg(t)/dtm).

Начальные условия: x(0),…, x(n-1)(0).

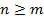– условие физической реализуемости.

Уравнения статики описывают установившийся режим, при котором все координаты объекта остаются неизменными во времени, то есть объект находится в состоянии равновесия. Они представляют собой алгебраические или дифференциальные уравнения, содержащие производные по какому-либо параметру, кроме времени. Существенной особенностью уравнений статики является неизменность координат объекта во времени. g(t)=const=g0, x(t)=const=x0.

Если g(t)=const=g0, то x(t)=const=x0. Тогда уравнение динамики преобразуется в уравнение статики:

a0* x0= b0* g0.

1

2.		Передаточные функции объектов и устройств управления.
g(t)			x(t)
	ЛДС (W(S))
G(S)			X(S)

Классический подход предполагает переход от временной области в область изображений. Преобразование Лапласа.

L[x(t)]=X(S) – линейный оператор. t – время, S – переменная Лапласа S=σ+jω. X(S)= ∫x(t)e-stdt (интеграл берётся от 0 до ∞).

x(t)=L-1[X(S)]=1/2πj*

Задача Коши.

Линеаризация возможна при малых возмущениях.

L[x1(t)]=S*X(S)-X(0+)

…

L[xn(t)]=Sn*X(S)-Sn-1*X(0+)- …-Xn-1(0+)

Теорема свертки: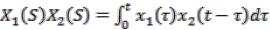

Применим преобразование Лапласа к ОДУ, описывающее ЛДС: anSnX(S)+an-1Sn-1X(S)+…+a1SX(S)+a0X(S)–Mн.у.(S)= =bmSmG(S)+bm-1Sm-1G(S)+…+ b1SG(S)+ b0G(S)

Начальные условия (n штук): x(0+),.., x(n-1)(0+) Положим начальные условия нулевыми. X(S)[anSn +…+ a0]= G(S)[bmSm+..+ b0]+Mн.у.(S)

X(S) = G(S) W(S)

W(S)= X(S)/G(S) – передаточная функция ЛДС – это отношение изображений выходного сигнала к входному при нулевых начальных условиях.

D(p) совпадает с D(S)

M(p) совпадает с M(S)

Передаточная функция может быть детализирована по 2-м направлениям: 1.типовые звенья 2.представление в виде нулей и полюсов

2

3. Основные характеристики типовых звеньев во временной и частотной областях.

g(t)	W(s)	x(t)
G(s)		X(s)

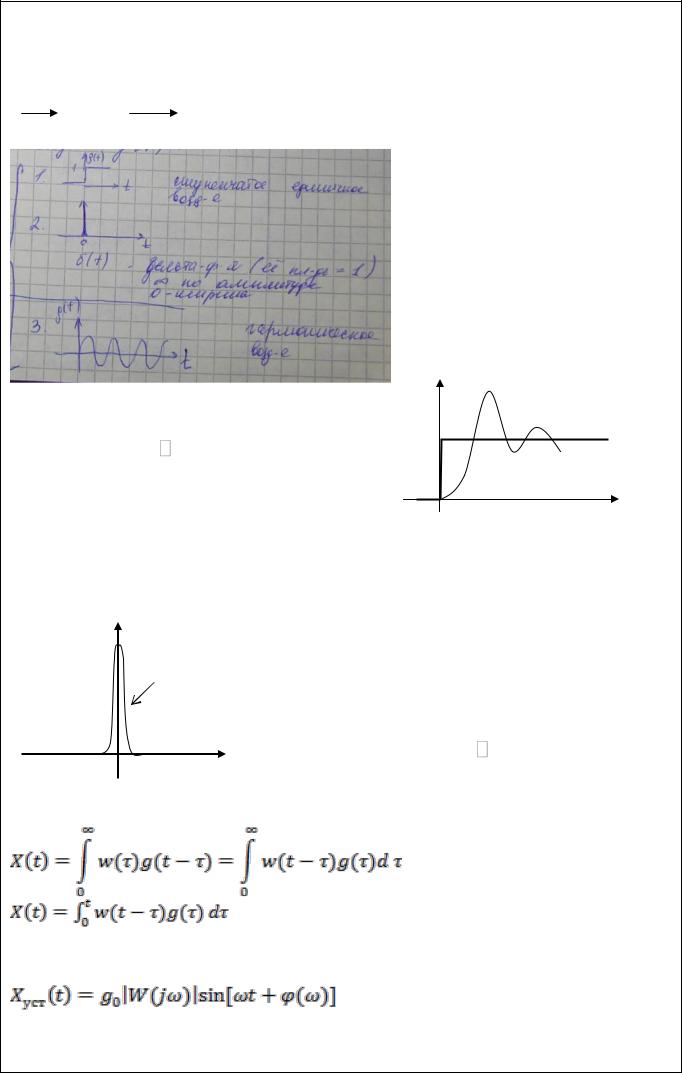
3 типа входных воздействий: - ступенчатое; - импульсное;

- гармоническое.

Переходная функция.

Реакция системы на ступенчатое входное воздействие называется

									переходной функцией (h(t)).
									g(t) {0,t 0} 1[t]
									1,t 0
	X (s)	W (s)							g(t)
				s
	x(t) L 1[ X (s)]					1		W (s)	est ds h(t)
						2 j		s
	(преобразование Лапласа)								t
	G(s)	1
				- единичное ступенчатое воздействие
		s

Весовая функция ЛДС.

Реакция системы на импульсное входное воздействие называется весовой функцией. g(t) = 1*(t-0)

	g(t)
			(t)dt 1
	(t)
			амплитуда бесконечна.
			L [ (t)] = 1
			G(s) = 1
		t	x(t) L 1[ X (s)] L 1[W (s)]	1	W (s)est ds w(t)
				2 j

w(t) – весовая функция ЛДС (импульсная переходная

функция).

– реакция имп. системы при нулевых начальных условиях.

Реакция на гармоническое воздействие

На вход подается гармоническое воздействие: g(t)=g0sin ωt, ω=const

3

Амплитудно-фазовая характеристика.

На вход подается гармоническое воздействие: g(t)=g0sin ωt, ω=const

			W ( j )	b	( j )m ... b	j b	P( ) jQ( )
W (s)				m	1	0
	s1	j		a	( j )n ... a	j a
				n	1	0

0 < +

P( ) – вещественная ЧХ, Q( ) – мнимая ЧХ. Амплитудно-фазовая ЧХ:

jv

Q( ) |W(j )|

( )>0

u

0

P(j )

Типичный случай АФЧХ: jv

k

u

	3		1
		2
			; ( ) argW ( j ) arctg	Q( )
	|W ( j ) |	P2 () Q2 ()
				P( )

4

4.Логарифмические частотные характеристики типовых звеньев, минимально-фазовые и неминимально-фазовые типовые звенья.

L( ) 20 lg w( j ) логарифмическая амплитудно-частотная хар-ка, дБ(децибел)

	W (S)	k(s	1 )...(s m )	i – полюсы 1,..n	i -нули 1,..m m<=n
		(s 1 )...(s n)

2

Наиболее часто встречающиеся звенья со множителем, типовые звенья: W (S) wi (s)

i 1

Типовые звенья делятся на минимально-фазовые(поведения амплитуды и фазы строго согласовано, есть закономерность) и неминимально-фазовые(несвязанны между собой, нет между ними закономерности).

Во всех графиках перегибы в точке 1/Т !

I. Минимально-фазовые звенья: (график: L(w) по вертикали и w,c-1 по горизонтали) 1) Усилительное звено

W(s)=k k>0,коэффициент передачи. Высота линии на рисунке 20lgk

2) Интегрирующее звено { L(w) 20log k * lg w }

W (s) ks

			Наклон -20дБ/декада
3) Апериодическое звено
W (s)	k		погрешность 3дБ
	Ts 1

4) Колебательное звено

	W (s)	k
		T 2 s 2 2 Ts 1

Если 0,4≤ζ≤0,7 погрешность =+/-3дБ при ζ=1 колебательное звено исчезает и появляется 2 апериодических 5) Дифференцирующее звено 1-го порядка

W (s) k( s 1)

5

6) Дифференцирующее звено 2-го порядка

W (s) k( 2 s2 2 s 1)

{7) Звено «чистого» дифференцирования (дифференцирующее звено)

W(s)=ks}

{Свойство минимально-фазовых звеньев +-n->+-(pi/2)*n} II. Неминимально-фазовые звенья:

1) Неустойчивое апериодическое звено

W (s) k Ts 1

2) Неустойчивое колебательное звено

W (s)	k	(присутствует как минимум один минус)
	T 2 s 2 2Ts 1

3)Дифференцирующее звено 1-го порядка

W(s)=k(1-τs)

4) Дифференцирующее звено 2-го порядка

W (s) k(1 2s 2 s2 )

5) Звено «чистого» запаздывания

W(S)=e-τs

6

5. Алгебраические критерии устойчивости.

Представим характеристическое уравнение системы в виде

an*Sn + an-1*Sn-1 + … + a1*S + a0 = 0

Критерий Рауса

1.в первой строке записываются коэффициенты уравнения с чётными индексами в порядке их возрастания

2.во второй строке — с нечётными

3.остальные элементы таблицы определяется по формуле: ,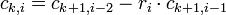

где 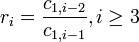— номер строки, — номер столбца 4. число строк таблицы Рауса на единицу больше порядка характеристического уравнения

Значения r	Номер	Номер столбца
	строки	1	2	3	…
-	1	an	an-2	an-4	…
-	2	an-1	an-3	an-5	…
r0=an/an-1	3	c13=an-2-r0*an-3	c23=an-4-r0*an-5	c33=an-6-r0*an-7	…
r1=an-1/c13	4	c14=an-3-r1*c23	c24=an-5-r1*c33	c34=an-7-r1*c43	…
r2=c13/c14	5	c15=c23-r2*c24	c25=c33-r2*c34	c35=c43-r2*c44	…
r3=c14/c15	6	c16= c24-r3*c25	c26=c34-r3*c35	c36=c44-r3*c45	…

Необходимым и достаточным условием того что все Reλi<0 (а значит и устойчивости) является положительность коэффициентов первого столбца.

{1+Kp*W(S)=0

Kp – предельный коэффициент усиления.}

Критерий Гурвица.

Из коэффициентов характеристического уравнения строится матрица Гурвица по алгоритму:

1)по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a[n-1] до a[0];

2)от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так,

чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше 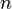ставятся нули.

an-1	an	0	0	…	0
an-3	an-2	an-1	an	… 0
an-5	an-4	an-3	an-2	…	0

…………………………………………………..

0 0 0 0 … a0

Необходимым и достаточным условием устойчивости является положительность всех диагональных миноров данной матрицы:

a[n-1], a[n-1]*a[n-2] – a[n-3]*a[n] и т.д.

Пример а)

при T1 = 0.1, T2 = 0.2.

7

Пример б)

при T1 = 0.1, T2 = 0.2.

8

6. Частотный критерий Найквиста.

Недостаток алгебраических методов состоит в том что по ним нельзя определить степень устойчивости. {Изменение аргумента для сомножителя соответствующего 1 т.е для полюсов: Re <0 приращение аргумента =+ , а для полюсов в правой полуплоскости = - .

Полное изменение аргумента arg D(j ) = i

arg D(j ) = arg(j - i)  изменение аргумента каждой из компонент n – порядок системы, m – колтчество полюсов в правой полуплоскости

arg(D(j ))=(n-m) -m =(n-2m) при изменяющемся от - до +

Для устойчивых систем m=0, arg(D(j ))=n . Если изменить диапазон (т.к отрицательных частот не бывает и Д(jw)симметрично отн-но вещ-ой оси), то получим при (0 + ) arg(D(j ))= n /2}

Критерий Найквиста

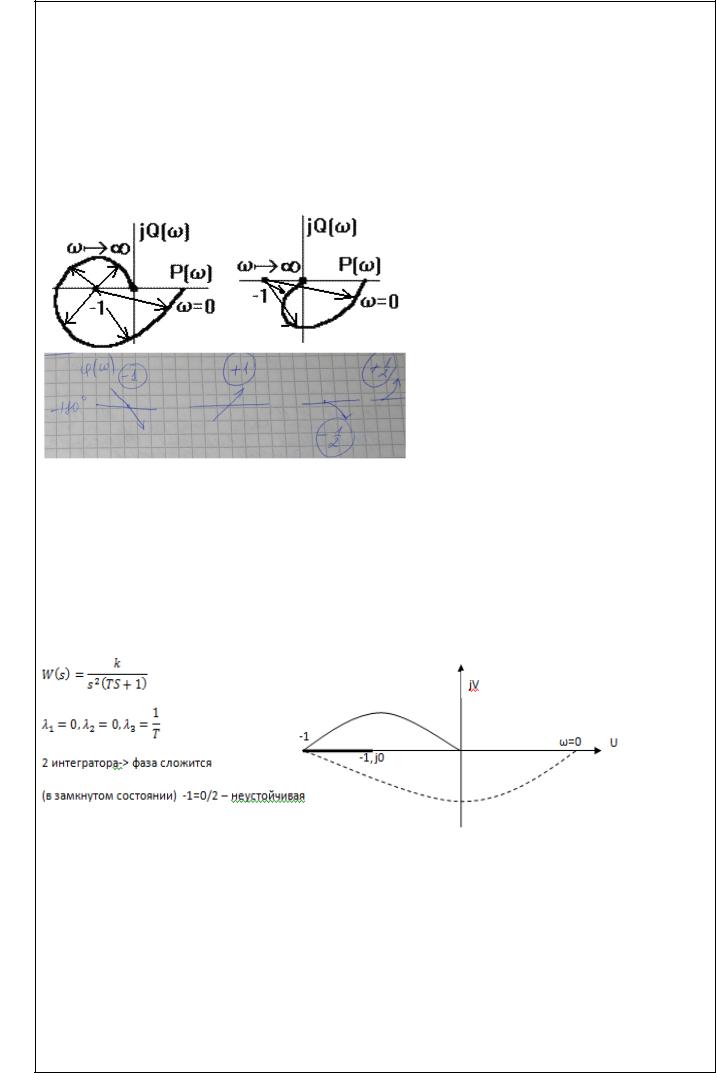
Для чтобы ЛДС была устойчива в замкнутом состоянии необх и достаточно чтобы ее годограф в разомкнутом состоянии охватывал критическую точку (- ;j0) при [0, + ] +m/2 раз, где m –

число полюсов разомкнутой системы в правой полуплоскости. Число охватов можно заменить числом пересечений. Достаточно рассмотреть отрезок вещественной оси (- ; (-1;j0)).

Критерий Найквиста: ЛДС уст в замкн сост общее число пеерходов АФЧХ разомкнутой сист через отрезок действительной оси (- ;-1) при изменении частоты от 0 до + было равным +m/2

Учет нулевого полюса будем считать что нулевой полюс находится в левой полуплоскости. Тогда заменим s на ej где 0, меняется от 0 до /2. Подставляем это в W(s) и получаем доопреджеление годографа, так чтобы он начинался на действительной оси.

Критерий Найквиста: Для того чтобы ЛДС была устойчивой в замкнутом сост. необх и дост чтобы общее число пересечений фазовой х-ки и оси (-180 -k*360 ) в области положительных амплитуд (L( )>0) при изменении частот от 0 до + было равным +m/2

∑число пересеч (-1800) = k/2, к – число полюсов системы в правой полупллоскости.

Пример:

9

7. Показатели качества систем управления.

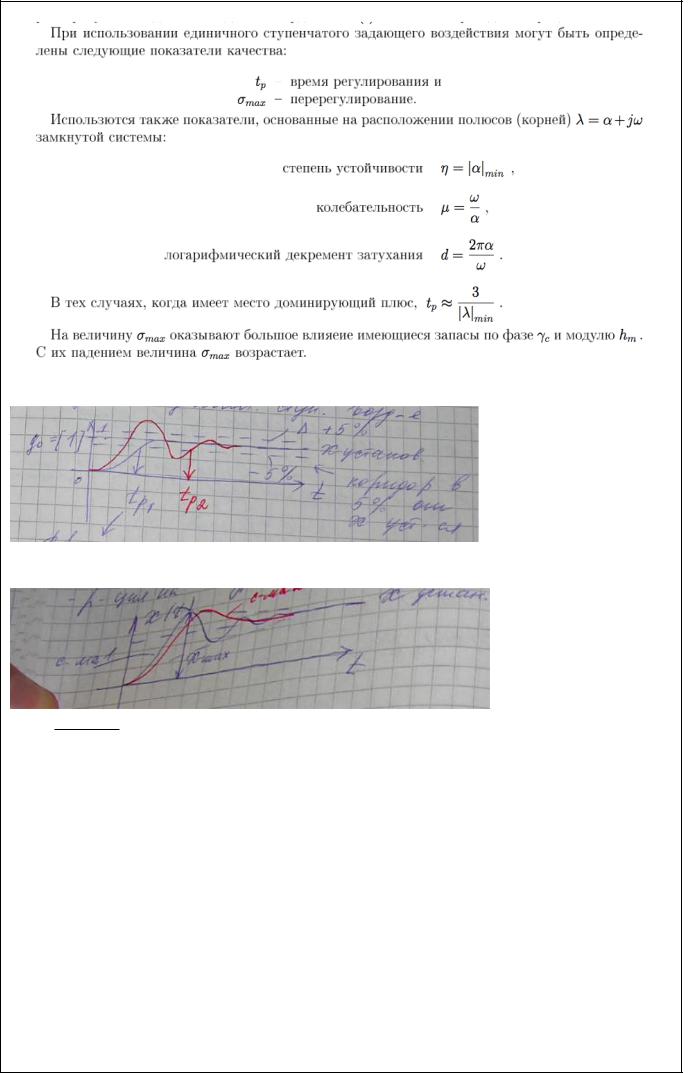
1)Время регулирования.

Подается ступенчатое воздействие.

tр – время вхождения в коридор (5 процентный), после которого функция уже не выйдет из него.

2) Перерегулирование – характеристика процесса , снабженная той или иной сигмой.

max xmax x( ) 100% .Чем ближе полюса к вещественной оси тем меньше xmax. x( )

Сигма и tp определяются полюсами. Расположение полюсов влияет на показатели качества. Чем ближе полюса, тем меньше колебательность. Чем меньше запасы, тем больше перерегулирование.

10