9.Вывод условий принципа максимума для нестационарных задач управления с интегральным критерием качества.

Пусть состояние динамической системы описывается нелинейным дифференциальным уравнением вида =(,,t)

А интегральный критерий качества зависит от времени:

Будем предполагать, что область цели тоже меняется со временем(нестационарна):

Считаем, что конечное время не задано.

Надо получить условия, которым удовлетворяет оптимальный процесс.

Введём в рассмотрение дополнительную переменную состояния, характеризующую изменение времени с начальным условием .

Тогда исходная система дифференциальных уравнений примет вид

Введём в рассмотрение расширенный вектор состояния из (n+1) компоненты.

Тогда задачу можно сформулировать как задачу оптимального управления системой вида

по интегральному критерию качества

Когда область цели задаётся так:

Мы свели нашу задачу к рассмотренной ранее стационарной системе, решение которой уже имеется.

Если — оптимальный процесс, то найдётся такая функцияи константатакие, что будут выполнятся следующие условия:

1.Условие максимума

2.Условие трансверсальности

Так как область начальных состояний от времени не зависит, условие трансверсальности в начале траектории не рассматривается.

3. Оптимальная траектория определяется решением системы канонических дифференциальных уравнений

a)

б)

4. Гамильтониан вдоль оптимальной траектории =0

Перепишем эти условия по отношению к переменным исходной задачи

1.Условие максимума (*) где

Так как явным образом от управления не зависит, условие максимума для эквивалентно условию максимума исходной системы

2.Условие трансверсальности.

Распишем условие трансверсальности, учитывая компоненты расширенных векторов

Условие трансверсальности исходной системы будет иметь вид

(90)

3.Распишем условие 3а), учитывая компоненты расширенных векторов.

(следует из (*))

Распишем условие 3б)

(тоже следует из (*)). Тогдаи(91)

4. Из условия 4 следует, что гамильтониан расширенной системы будет определяться как. =0 Находим из этого соотношения чему будет равен гамильтониан исходной системы:(92)

Проинтегрируем выражение (91):(93)

Выразим из полученного выражения функцию .

Подставим функцию в выражение (92):

, где-условие трансверсальности для. Получили выражение для гамильтониана вдоль оптимальной траектории нестационарной задачи. Если считать, что конечное время задано, условие принципа максимума сохранится за исключением 4-го условия. Так как время фиксировано, а область цели связана с конечным временем движения системы, считаем, что в задаче с фиксированным временем область цели от времени не зависит.

Подставим значение для 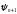из (92) в соотношение (93). Тогда имеем

Отсюда видно, что если задача нестационарна с фиксированным временем движения, то для этой задач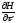и=0, и, следовательно, гамильтониан вдоль оптимальной траектории будет константой.

Вывод: для нестационарных задач управления с интегральным критерием качества, если конечное время нефиксированно, гамильтониан как функция времени равен нулю, а если фиксированно — то постоянной.