11.1 Определение второго замечательного предела

Вторым замечательным пределом называется предел:

(11.1)

Или, грубо говоря, .

11.2 Следствия из второго замечательного предела

1.

2.

3.

4.

5.

6.

7.

Из равенств 3 и 4 получим дополнение к таблице эквивалентных бесконечно малых величин при :

ЛЕКЦИЯ 13

Производная функции одной переменной

13.1 Определение приращения функции

Рассмотрим функцию , непрерывную на некотором отрезке. Рассмотрим два значения аргумента этой функции: исходноеи новое.

Разность называетсяприращением аргумента в точке .

Обозначение:

При этом приращением функции в точке называется разность .

Обозначение:

Из равенств: инайдем переменныеи.

(13.1)

Следовательно, можем записать:

(13.2)

13.2 Определение производной функции

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента,

Когда приращение аргумента стремится к нулю.

Обозначения:

Таким образом, по определению –

(13.3)

Механический смысл производной:

Пусть материальная точка движется по прямой, в одном направлении, по закону , где- время,- путь, проходимый этой точкой за время. Тогда, скоростьданной точки в момент времениесть производная от путипо времени.

(13.4)

Геометрический смысл производной:

Угловой коэффициент касательной к графику функции в точке равен производной данной функции в этой точке.

(13.5)

13.3 Свойства производной функции

13.4 Производные основных функций

13.5 Производные обратных функций

Теорема Если функция на некотором промежутке числовой прямой непрерывна, дифференцируема и имеет в некоторой точке данного промежутка отличную от нуля производную, то функция,обратная этой функции, в соответствующей точке также имеет производную. Причем, производная обратной функции равна .

Доказательство

Рассмотрим функцию . Обратной является функция. Следовательно,

.

Таким образом,

(13.6)

Найдем производные обратных тригонометрических функций.

1.

Таким образом,

2.

Таким образом,

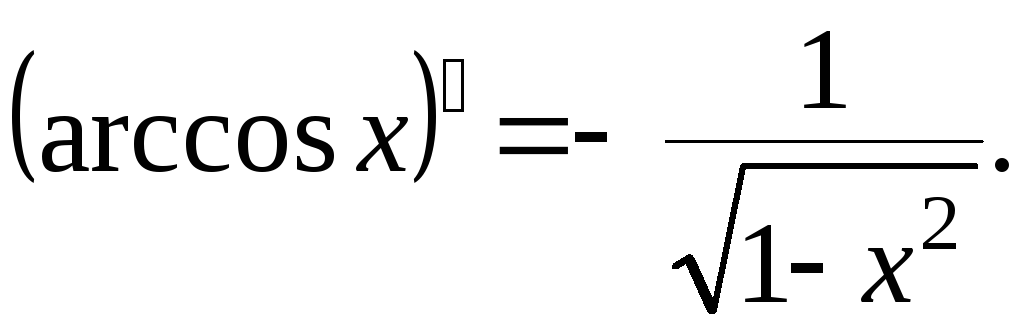
3.

Таким образом,

4.

Таким образом,

ЛЕКЦИЯ 14

Гиперболические функции. Их производные

14.1 Определение гиперболических функций

1. Гиперболический синус

(14.1)

Область определения: .

Множество значений: .

y

0 x

2. Гиперболический косинус

(14.2)

Область определения: .

Множество значений: .

y

1

0 x

3. Гиперболический тангенс

(14.3)

Область определения: .

Множество значений: .

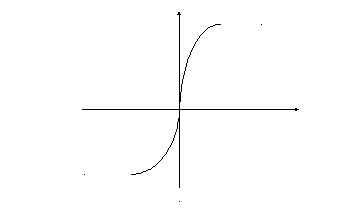
y

0 x

4. Гиперболический котангенс

(14.4)

Область определения: .

Множество значений: , т.к.:

y

0 x