
- •1.6 Полярная и цилиндрическая системы координат
- •1. Полярная система координат.
- •1. Цилиндрические координаты точки в пространстве.
- •2.1 Понятие вектора
- •4.3 Проекция вектора на направление другого вектора
- •5.1 Определение векторного произведения
- •5.2 Вычисление векторного произведения двух векторов
- •5.3 Свойства векторного произведения
- •7.2 Плоскость
- •7.3 Прямая в пространстве
- •7.4 Взаимное расположение прямых и плоскостей в пространстве
- •8.1 Определение предела
- •8.2 Свойства пределов
- •8.3 Бесконечно малые и бесконечно большие величины
- •8.4 Первый замечательный предел
- •9.1 Определение функции одной переменной
- •9.2 Способы задания функции
- •9.3 Основные свойства функции
- •9.4 Основные элементарные функции. Их графики
- •10.1 Односторонние пределы
- •10.2 Определение непрерывности функции
- •10.2 Классификация точек разрыва функции
- •11.1 Определение второго замечательного предела
- •11.2 Следствия из второго замечательного предела
- •13.1 Определение приращения функции
- •13.2 Определение производной функции
- •13.3 Свойства производной функции
- •13.4 Производные основных функций
- •13.5 Производные обратных функций
- •14.1 Определение гиперболических функций
- •14.2 Производные гиперболических функций
- •14.3 Производные сложных функций
- •14.4 Производные высших порядков
- •15.1 Параметрическое задание функций
- •15.2 Производные параметрических функций
- •15.3 Уравнения касательной и нормали к графику функции в заданной точке
- •16.1 Определение дифференциала. Его геометрический смысл
- •16.2 Свойства дифференциала
- •17.4 Теорема Лагранжа
- •17.5 Правило Лопиталя
- •17.6 Производная от функции в степени функции
- •18.1 Определение экстремума
- •18.2 Условия существования экстремума
- •18.3 Наибольшее и наименьшее значения функции на отрезке
- •18.4 Точки перегиба графика функции
- •19.1 Вертикальные асимптоты
- •19.2 Наклонные асимптоты
- •20.1 Определение степенного ряда
- •20.2 Ряд Тейлора
- •20.3 Ряд Маклорена
14.2 Производные гиперболических функций
Заметим сначала, что:

![]() (14.5)
(14.5)
1.
 .
.
2.
 .
.
3.
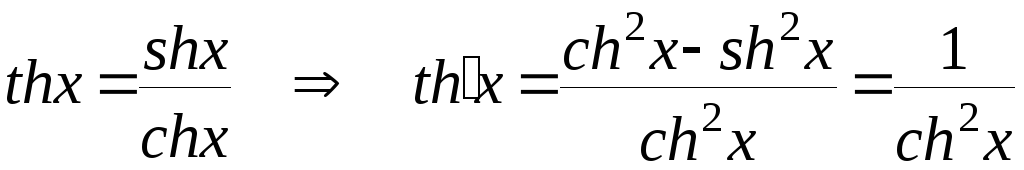 .
.
4.
 .
.
Таким образом, дополним таблицу производных формулами:

14.3 Производные сложных функций
Если заданная функция имеет вид:
![]() ,
то производная этой функции равна
произведению
производной внешней функции
,
то производная этой функции равна
произведению
производной внешней функции
![]() попромежуточному
аргументу
попромежуточному
аргументу
![]() на производную этого промежуточного
аргумента. Таким образом, можем записать:
на производную этого промежуточного
аргумента. Таким образом, можем записать:
![]() (14.6)
(14.6)
Пример. Найти производную функции
![]() .
.
Решение

14.4 Производные высших порядков
Производной второго порядка называется производная от первой производной.
Производной третьего порядка называется производная от второй производной. И т.д.
ЛЕКЦИЯ 15
Функции, заданные параметрически. Их производные
15.1 Параметрическое задание функций
Одним
из способов задания функции является
такой способ, при котором текущие
координаты
![]() и
и![]() рассматриваются как функцииодних
и тех же значений
третьей переменной величины:
рассматриваются как функцииодних
и тех же значений
третьей переменной величины:
 (15.1)
(15.1)
При
этом, уравнения (15.1) называются
параметрическими уравнениями некоторой
линии на плоскости,
а переменная
![]() называетсяпараметром.
называетсяпараметром.
Примеры параметрических уравнений некоторых известных линий:
ОКРУЖНОСТЬ:
 (15.2)
(15.2)
ЭЛЛИПС:
 (15.3)
(15.3)
ЦИКЛОИДА:
 (15.4)
(15.4)
Циклоидой
называется
линия, описываемая окружностью с центром
в точке
![]() ,
радиуса
,
радиуса![]() ,
катящейсябез
скольжения по
оси абсцисс.
,
катящейсябез
скольжения по
оси абсцисс.


![]()
О
![]() х
х
15.2 Производные параметрических функций
Рассмотрим функцию, заданную параметрическими уравнениями:


Таким образом, получили формулу:
 (15.5)
(15.5)
Найдем вторую производную параметрической функции:

Таким образом, получили формулу:
 (15.6)
(15.6)
Темы: «Дифференцирование неявных функций» и «Логарифмическое дифференцирование» Рассматриваются на практических занятиях!
15.3 Уравнения касательной и нормали к графику функции в заданной точке
Рассмотрим
функцию
![]() ,
непрерывную на некотором промежутке
,
непрерывную на некотором промежутке![]() .
Найдем уравнение касательной к графику
этой функции в точке
.
Найдем уравнение касательной к графику
этой функции в точке![]() ,
принадлежащей данному промежутку.
Воспользуемся известным уравнением
прямой на плоскости, проходящей через
заданную точку с заданным угловым
коэффициентом. При этом, из геометрического
смысла производной известно, что угловым
коэффициентом касательной является
производная данной функции, вычисленная
в точке касания. Следовательно, искомым
уравнением является уравнение:
,
принадлежащей данному промежутку.
Воспользуемся известным уравнением
прямой на плоскости, проходящей через
заданную точку с заданным угловым
коэффициентом. При этом, из геометрического
смысла производной известно, что угловым
коэффициентом касательной является
производная данной функции, вычисленная
в точке касания. Следовательно, искомым
уравнением является уравнение:
![]() (15.7)
(15.7)
Нормалью
графика функции в точке
![]() называется прямая, проходящая через
эту точку, перпендикулярно касательной
в данной точке. Следовательно, уравнение
нормали:
называется прямая, проходящая через
эту точку, перпендикулярно касательной
в данной точке. Следовательно, уравнение
нормали:
 (15.8)
(15.8)
ЛЕКЦИЯ 16
Дифференциал
