Задачи для самостоятельного решения

1. Найти поток векторного поля через внешнюю поверхностьS конуса

2. Найти поток векторного поля через верхнюю поверхностьS полусферы .

Ответы

1.  . 2.  .

Занятие 5 Формула Остроградского – Гаусса. Дивергенция

Пример. Найти поток вектора напряженности электростатического поля точечного заряда

через замкнутую поверхность, охватывающую начало координат – точку расположения заряда.

Решение. Сначала найдем поток нашего поля через сферическую поверхность .

.

Так как наше поле и сферическая поверхность симметричны относительно начала координат, в каждой точке поверхности вектор направлен параллельно единичному вектору нормали, а модуль вектораравен, поэтому скалярное полеравнои его можно вынести из-под интеграла.

При вычислении интеграла мы воспользовались формулой площади поверхности шара Можно показать, что такой же результат получится для любой замкнутой поверхности, охватывающей начало координат. Если мы будем вычислять поток нашего поля через замкнутую поверхность, не охватывающую начало координат, по формуле Остроградского - Гаусса то получим нулевой поток, так как дивергенция электростатического поля равна нулю во всех точках кроме начала координат. Область с выколотой точкой не является объемно-односвязной и формула Остроградского – Гаусса не применима для поверхностей, охватывающих выколотую точку (в нашем случае начало координат).

Пример. Найти поток вектора через поверхность части конуса, отсекаемой плоскостью и, в отрицательном направлении орта.

Решение. Воспользуемся формулой Остроградского-Гаусса. Для этого замкнем коническую поверхность, добавив к ней круг радиуса , лежащий в плоскости. Согласно формуле Остроградского-Гаусса, поток полячерез полученную замкнутую поверхность будет определяться тройным интеграломпо конусу. Учитывая, что, тройной интеграл, а, значит, и поток поля через замкнутую поверхность будет равен утроенному объему конуса. (Радиус основания нашего конуса равен, высота конуса также равна.) Теперь вычислим поток поля через замыкающую поверхность (круг радиуса), в положительном направлении орта. Этот поток определяется поверхностным интегралом второго рода

,

где ,и– проекции круга на координатные плоскости. Учитывая, что площадь только проекциине равна нулю и, что значение функциина замыкающем круге равно, получаем поток через замыкающую поверхность. Видим, что поток векторного полячерез замыкающую поверхность равен потоку через всю замкнутую поверхность, то есть поток поля через коническую поверхность равен нулю. Этот результат можно было получить сразу без вычислений. Векторными линиями нашего поля являются лучи, выходящие из начала координат. Они касаются конической поверхности во всех точках. Это значит, что полево всех точках конической поверхностиперпендикулярно единичному вектору нормалии его поток через эту поверхность равен нулю.

Пример. Найти поток вектора через поверхность части параболоида, отсекаемой плоскостью, в отрицательном направлении орта.

Решение. Также как и в предыдущем примере замкнем параболическую поверхность, добавив к ней круг радиуса , лежащий в плоскости. Согласно формуле Остроградского-Гаусса, поток полячерез полученную замкнутую поверхность будет определяться тройным интеграломпо множеству, заключенному внутри замкнутой поверхности. Для вычисления тройного интеграла перейдем к цилиндрической системе координат,,. Учитывая, что, тройной интегралсводим к повторному

.

Теперь вычислим поток поля через замыкающую поверхность, в положительном направлении орта . Этот поток определяется поверхностным интегралом второго рода

,

где ,и– проекции круга на координатные плоскости. Учитывая, что площадь только проекциине равна нулю и, что значение функциина замыкающем круге равно, получаем поток через замыкающую поверхность.

Чтобы получить значение потока через параболическую поверхность надо из потока через замкнутую поверхность вычесть поток через замыкающую поверхность. Окончательно получаем.

Пример. Получить формулу Гаусса - поток напряженности электрического поля через замкнутую поверхностьравен всему заряду, заключенному внутри этой поверхности, деленному на электрическую постоянную вакуума.

Решение. Как мы уже знаем (см. пример 4.45), поле точечного заряда , помещенного в начало координат, определяется выражением

.

В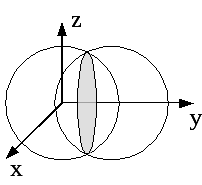ычислить поток этого поля через замкнутую поверхность с зарядомвнутри по теореме Остроградского-Гаусса невозможно, так как поле в точке расположения заряда не определено (область, включающая начало координат, не является объемно-односвязной и теорема Остроградского-Гаусса для нее не применима). Если замкнутая поверхностьявляется сферой с центром в начале координат, то поток напряженности электрического поля вычисляется непосредственно через поверхностный интеграл второго рода. Он равен. Сместим теперь сферу относительно начала координат в какую-нибудь сторону на произвольное расстояние, не превышающее радиус сферы. Получим область, ограниченную поверхностямии, и область, ограниченную поверхностямии. Эти области объемно-односвязные. Запишем дляформулу Остроградского-Гаусса. Тройной интеграл по областиравен нулю, так какравна нулю во всех точках кроме начала координат. Значит правая часть формулы Остроградского-Гаусса равна нулю, то есть поток полячерез поверхностьравен потоку через поверхность. Применяя формулу Остроградского-Гаусса к области, получим, что поток полячерез поверхностьравен потоку через поверхность. Так как несмещенная сфера образована поверхностямии, а смещенная поверхностямии, то потоки полячерез эти сферы одинаковы и равны. Таким образом, поток поля точечного заряда через сферу не зависит от точки расположения заряда внутри сферы. Деформируя нашу сферу произвольным образом добавлением и вычитанием областей,,и т.д., распространим этот результат на любую замкнутую поверхность. Используя аддитивность полей и их потоков (принцип суперпозиции) рассматриваем не один, а много зарядов и получаем теорему Гаусса - поток напряженности электрического поля через любую замкнутую поверхностьравен всему заряду, заключенному внутри этой поверхности, деленному на электрическую постоянную вакуума.