Задачи для самостоятельного решения

В задачах 16 – 30 исследовать сходимость числового ряда с общим членом u_n .

16. . 17. . 18. .

19. . 20. .

21. .22. .23. .

24. .25. .26. .

27. .28. .29. .

30. .

Ответы

16. Сходится. 17. Сходится. 18. Сходится. 19. Сходится при а < e. 20. Сходится при a > e. 21. Сходится при p > 1. 22. Сходится при р > 1. 23. Сходится. 24. Сходится при α > 1. 25. Расходится. 26. Сходится. 27. Сходится. 28. Сходится. 29. Сходится. 30. Сходится.

Знакочередующиеся ряды. Признак Лейбница

Пример. Проверить выполнение условий теоремы Лейбница для ряда . В случае положительного ответа оценить.

Решение. Так как и последовательностьмонотонно убывает, то условия теоремы Лейбница выполнены. Поэтому справедлива оценка остатка ряда по модулю

.

Ответ: удовлетворяет предположениям теоремы Лейбница..

Условная сходимость. Признак Абеля-Дирихле

Пример. Исследовать сходимость ряда .

Решение. Для исследования абсолютной сходимости рассмотрим ряд . Как известно (пример 2.7.2), гармонический рядрасходится. Поэтому у исходного ряда нет абсолютной сходимости. Однако как показано в примере 2.7.1 исходный ряд удовлетворяет предположениям теоремы Лейбница. Поэтому ряд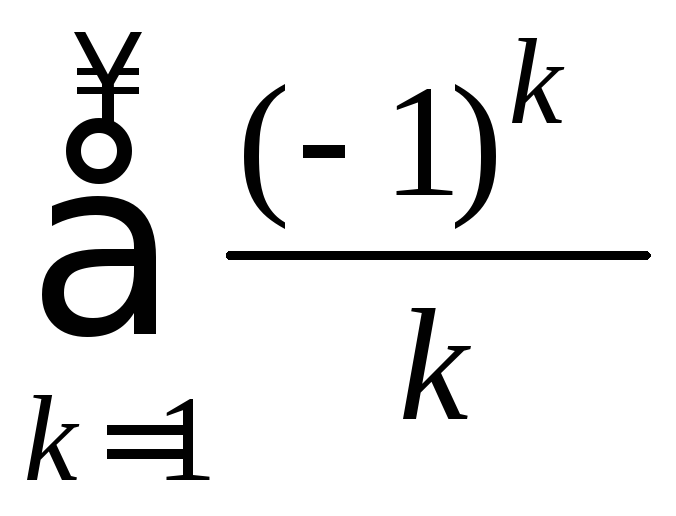сходится.

Ответ: сходится условно.

Для проверки условной сходимости, помимо признака Лейбница, применяются также следующий признак:

Пример. Для произвольно заданного вещественного числа доказать равномерную ограниченность последовательности частичных суммряда.

Решение. Заметим, что . Поэтому для частичной суммы имеет место равенство

.

Для частичной суммы геометрической прогрессии (независимо от знаменателя) справедливо равенство:

.

Поэтому

Следовательно,

.

Отсюда

при всех .

Ответ: .

Пример. Для произвольно заданного вещественного числа доказать равномерную ограниченность последовательности частичных суммряда.

Решение. Заметим, что . Поэтому для частичной суммы имеет место равенство

.

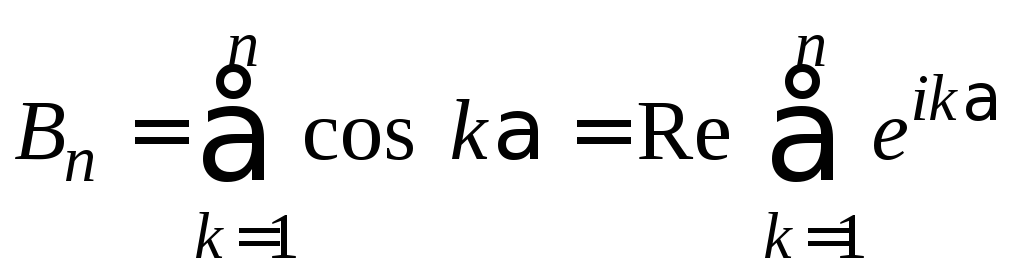Запишем частичную сумму геометрической прогрессии по формуле:

.

Отсюда

Следовательно,

.

Отсюда

при всех .

Ответ: .

Пример. Исследовать сходимость ряда .

Решение. Как показано в примере 2.3.2 ряд расходится. Поэтому расходится ряд.

Отсюда нет абсолютной сходимости у ряда 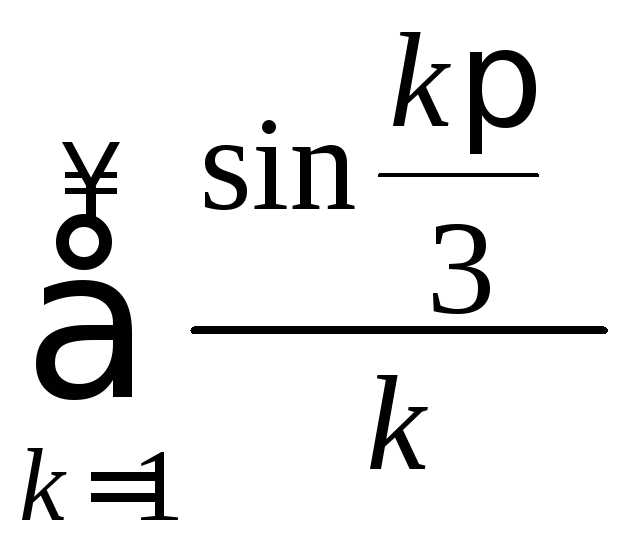. Исследуем условную сходимость по признаку Абеля – Дирихле. Как показано в примере 2.8.2, частичные суммы рядаравномерно ограничены числом. Кроме того, последовательностьмонотонно стремится к. Следовательно, рядсходится по признаку Абеля–Дирихле.

Ответ: сходится условно.

Задачи для самостоятельного решения

В задачах 31 – 45 исследовать абсолютную сходимость числового ряда с общим членом u_n.

31. . 32. . 33. .

34. .35. . 36. .

37. . 38. .

39. . 40. .

41. . 42. .

43. . 44. .

45. .

Ответы

31. Сходится не абсолютно. 32. Сходится абсолютно. 33. Расходится. 34. Сходится абсолютно при α > 1; сходится не абсолютно при 0 < α ≤1; расходится при α ≤ 0. 35. Сходится не абсолютно. 36. Сходится абсолютно. 37. Сходится абсолютно. 38. Сходится абсолютно. 39. Сходится не абсолютно. 40. Сходится абсолютно. 41. Сходится абсолютно. 42. Сходится абсолютно. 43. Сходится абсолютно. 44. Сходится не абсолютно. 45. Сходится абсолютно.