9.3 Прямолінійно-паралельний потік пружної рідини

Розглянемо одновимірний прямолінійно-паралельний потік пружної рідини з напівнескінченного пружного пласта до прямолінійної галереї (рис. 9.7, а). Диференціальне рівняння в цьому випадку набуває вигляду:

. (9.26)

Точні розв’язки цього рівняння дістанемо за умов заданих постійної депресії тиску та постійного дебіту. Задача зводиться до визначення або тиску в будь-якій точці пласта і в будь-який момент часу (чи інакше розподілу тиску в пласті на різні моменти часу) та дебіту галереїабо тиску на стінці галереї.

Задано постійну депресію тиску , тобто. Початкова та граничні умови щодо тискумають вигляд:

(9.27)

Задача може бути розв’язана різними методами. Розв’язок легко отримується на основі аналізу розмірностей. Вводимо безрозмірний тиск

, (9.28)

звідси для умовиідля умови.

Як видно з рівнянь (9.26) і (9.28), безрозмірний тиск залежить відх, t, , тобто. Розмірності цих величин такі:;;. Оскільки маємо три розмірні величини, а серед них є дві величиниз незалежними розмірностями, то згідно з - теоремою з цих величин складаємо один безрозмірний комплекс (маємо: 3 – 2 = 1)

. (9.29)

Для зручнішого подання розв’язку вводимо в рівняння (9.29) постійне число 2, тобто беремо

. (9.30)

при цьому та.

Задача автомодельна, оскільки шуканий тиск залежить тільки від одної змінної, тоді

. (9.31)

Замінюємо тиск р на безрозмірний тиск згідно з рівнянням (9.28), а тоді рівняння (9.26) набуває вигляду:

. (9.32)

За правилом диференціювання складних функцій із виразу (9.31) з урахуванням рівняння (9.30) маємо:

;

;

,

де ;.

Підставляючи знайдені величини ,у рівняння (9.32), одержуємо звичайне диференціальне рівняння:

,

або після спрощення

. (9.33)

При цьому необхідні перші дві умови (9.27) переходять у такі:

. (9.34)

Для розв’язування рівняння (9.33) позначаємо

, (9.35)

тоді рівняння (9.33) записується:

.

Розділивши змінні, знаходимо:

;

;

;

;

, (9.36)

де с₁, с₂ – постійні інтегрування.

Рівняння (9.36) є загальним розв’язком задачі. Знаходимо постійні с₁ і с₂ з умов (9.34):

(9.37)

де , а тоді

;.

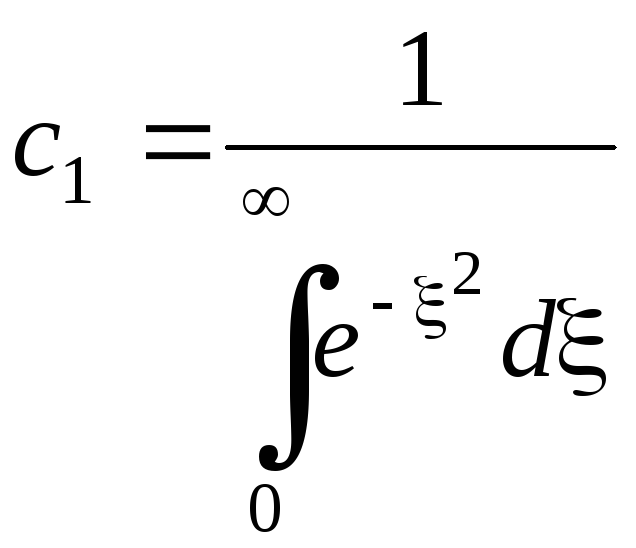Оскільки з інтегрального числення відомо, що

,

то

.

Отже, закон розподілу тиску в пласті за заданої постійної депресії тиску має вигляд:

, (9.38)

або з урахуванням рівняння (9.28)

, (9.39)

де функція називається інтегралом або функцією ймовірностей (функція табульована – подана в таблицях; змінюється в межах від 0 задо 1 за).

Якщо ввести на відміну від рівняння (9.28) інший безрозмірний тиск

, (9.40)

то закон розподілу тиску в пласті за заданої постійної депресії тиску набуде ще й такого вигляду:

, (9.41)

або

. (9.42)

Відзначимо, що в цих розв’язках замість x можна задавати (x – x₀), де x₀ – координата розміщення галереї.

Витрату рідини через поперечний переріз пласта площею F знаходимо, підставляючи похідну із рівняння (9.39) чи (9.42) у формулу закону Дарсі:

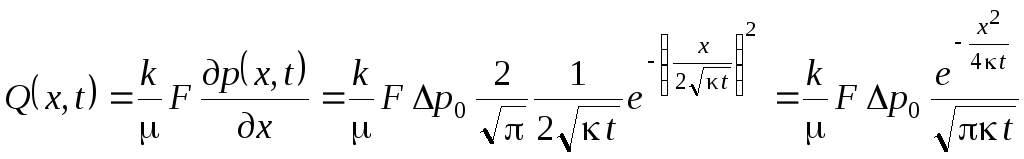. (9.43)

Тут взято знак “+”, оскільки з ростом координати х збільшується тиск р, тобто потік рухається проти осі ОХ.

Поклавши в рівнянні (9.43) , дістаємо формулу дебіту галереї:

, (9.44)

або

, (9.45)

де параметр

(9.46)

є монотонно згасаючою функцією, тобто Q_t в часі зменшується або за, а в початковий момент часудебіт, що є наслідком стрибка тиску на стінці галереї від. Е.Б. Чекалюк запропонував її назвати функцією продуктивності галереї, або функцією припливу.

Якщо позначити

, (9.47)

то формула (9.28) набуде вигляду формули дебіту галереї за усталеної фільтрації. А за неусталеної фільтрації характеризує розмір зони пласта, де має місце рух рідини, або інакше, розмір збуреної зони, причомуза, а.

Розподіл тиску p в напівнескінченному пласті за умови на різні моменти часуt показано на рис. 9.7, б.

Накопичений відбір рідини на момент часу t буде:

(9.48)

тобто є монотонно зростаючою в часі функцією.

2. Задано постійний дебіт галереї .

Початкові та граничні умови в цьому випадку записуємо через швидкість фільтрації v у вигляді:

(9.49)

де

Для зведення диференціального рівняння (9.26) і крайових умов (9.49) до одних змінних величин, тобто до , множимо рівняння (9.26) наі беремо похідну пох, тоді маємо:

;

;

;

, (9.50)

оскільки (взято знак “+”, так як з ростом координатих збільшується тиск р).

Рівняння (9.50) за формою збігається з рівнянням (9.26), а отже загальним розв’язком його буде рівняння (9.36), записане через швидкість фільтрації:

, (9.51)

або

, (9.52)

так як крайові умови мають такий вигляд

для; (9.53)

для,

а постійні інтегрування тоді дорівнюють

;.

Для одержання розподілу тиску в пласті необхідно проінтегрувати рівняння (9.52) пох, вважаючи, що , аt зафіксовано, тобто

Звідси маємо:

Останній доданок інтегруємо частинами, а саме:

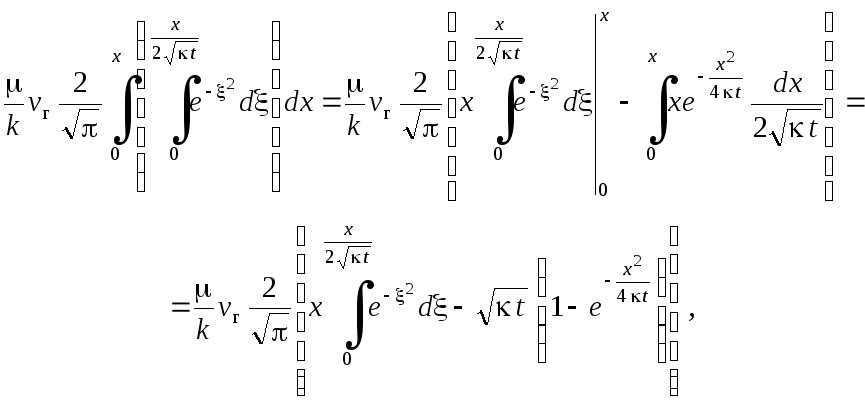
тобто записуємо де;

Тоді в цілому отримуємо:

(9.54)

де ;.

Звідси за ,маємо рівняння розподілу тиску в пласті для випадку заданого дебіту:

. (9.55)

Оскільки для, то із рівняння (9.55) одержуємо формулу тиску на стінці галереї за заданого дебіту. Для цього спочатку в рівняння (9.51) підставляємо граничну умовудлях  . Так як для х   інтеграл імовірностей , то добутокдає невизначеність · 0. Розкриваючи цю невизначеність за правилом Лопіталя, отримуємо, що цей добуток прямує до нуля за х  . Враховуючи, що , отримуємо формулу:

,

звідки тиск на стінці галереї

(9.56)

або депресія тиску

, (9.57)

а дебіт галереї тоді виражається так:

, (9.58)

де (9.59)

є функцією депресії тиску за аналогією з функцією продуктивності ;

. (9.60)

Оскільки зростає у часі, то із формули (9.58) виходить, що для забезпечення постійного дебітутреба збільшувати депресію тиску, тобто зменшувати тискр_г. Але це можливо до певної межі (тиск насичення нафти газом р_нас, руйнування пласта і т. ін.). Тому через деякий час треба переходити до умови постійної депресії тиску , тоді зменшуватиметься дебіт галереїQ_t (рис. 9.7, в).