Билет 19. Вопрос 1. Связь момента импульса твёрдоготела с угловой скоростью еговращения. Тензор инерции. Главные и центральные оси инерции. Оси свободного вращения.

Момент импульса. Тензор инерции.Момент импульса тела относительно неподвижной точки – важнейшее понятие в динамике вращательного движения твердого тела. Он определяется так же, как и для системы материальных точек:

Здесь p_i=m_iv_i– импульс элементарной массыdm_iв лабораторной системе XYZ, а r_i– радиус-вектор массыdm_iс началом в той неподвижной точке, относительно которой вычисляется момент импульса тела. С учетом постоянства расстояний между точками абсолютно твердого тела вектор момента импульса L удается связать с вектором угловой скорости w.Рассмотрим, к примеру, две одинаковые точечные массы m, укрепленные на концах невесомого стержня АВ (рис. 2.3). Стержень с массами вращается с угловой скоростью w вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае:

L=mr_iv_i+mr₂v₂=2mr², здесь учтено, что:r₁=r₂=r, аv₁=v₁=r.

Существенно, что в этом примере век тор L направлен так же, как и. К сожалению, так бывает не всегда. В этом можно убедиться на примере, показанном на рис. 2.4. Получим выражение для L в случае твердого тела произвольной формы, закрепленного в некоторой точке О. Пусть r_i– радиус-вектор элементарной массыm_iтвердого тела, а–угловая скорость. Тогда:

Векторы r_i,  и L можно проектировать как на оси лабораторной системы XYZ, так и на оси системы xyz, жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы xyz заключается в том, что в ней проекции r i являются постоянными величинами (в системе XYZ они зависят от времени), и выражения для компонент L оказываются проще.

ываются центробежными моментами инерции. ЕслиJ_xy=J_yx,J_xz=J_zx,J_zy=J_yz, то тензор наз. симметричным.

Если оси Ox,Oy,Ozсовместить с главными осями инерции, то тензор инарциипримет дигональный вид. ВеличиныJ_xx=J_x,J_yy=J_y,J_xx=J_zв этом случае наз. главными моментами инрции тела, причём:L_x=J_x_xи т. д. Эти оси также называютсяглавными осями тензора инерции. Они жестко связаны с телом.

Направление главных осей тела часто можно определить, пользуюсь соображениями симметрии. Так, например, главные оси однородного прямоугольного параллелепипеда параллельны его рёбрам. К телам такого рода относится, например цилиндр.

Оси свободного вращения.Вращательное движение – это такое, при котором две точки тела остаются всё время неподвижными. Прямая, проходящая через эти точки, называетсяосью вращения.Все точки твердого тела, лежащие на оси вращения, неподвижны. Другие точки твердого тела движутся по окружностям в плоскостях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения. Вращательное двизение твердого тела является плоским.

Вопрос 2. Колебания системы с двумя степенями свободы. Нормальные колебания(моды). Нормальные частоты. Примеры.

Если система обладает несколикими слепенями свободы, то при малых отклонениях от положения равновесия возможны колебания сразу по всем степеням свободы. Обычный маятник может колебаться в двух взаимо перпендкудярных вертикальных плоскостях, проходящих через точку подвеса. Поэтому он имеет две степени свободы. Наличие связи раздичных степеней свободы между собой придает колебанию системы со многими степенями свободы новые физические закономерности.

С

k

k1

k

вязанной системойназывается система со многими степенями свободы,между которыми имеется связи, обеспечивающие возможность обмена энергией между различными степенями свободы. Примером связанной системы с двумя степенями свободы могут служить два маятника, соединенных между собой пружиной.

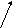
пружина

два пружинных маятника

x1

x2

Несмотря на сложность движения двух связанных маятников, оно всегда может быть представлено как суперпоизция четырех гармонических колебаний, частоты которых называются нормальными частотамисвязанной системы. Число нормальных частот равно числу степеней свободы. В приведенном примере имеем две степени свободы. И можно представить колебание как суперпозицию двух колебаний.

ωI S^I₁(t)=S20sin(ω_I*t+φ_I)

S^I₂(t)=S₁₀sin(ω_I*t+φ_I)

ωI,S^I20/S^I10=1 – первая мода

ωI=√(k/m)

ωIIS^II₁(t)=S^II20*sin(ω_II*t+φ_II)

S^II₂(t)=S^II_10*sin(ω_II*t+φ_II)

ωII,S^II20/S^II₁₀ = -1 – вторая мода

ωII=√((k+2k1)/m)

S₁(t)=S^I10*sin(ω_I*t+φ_I)+S^II10*sin(ω_II*t+φ_II)

S₂(t)=S^I20*sin(ω_I*t+φ_I)+S^II20*sin(ω_II*t+φ_II)

ωI,ωII, S^I20/S^I10, S^II20 / S^II₁₀ } известны

Начальные условия S1(0),S1^'(0)

S₂(0),S₂^'(0)} →S^I10;φ_I

S^II10;φ_II

Еслимаятинки отклонить одинаково в одну сторону, то они колеблются с некоторой частотой ω1, которая называется нормальной. Частота колебаний маятников, отклоненных одинаково в противоположных направлениях, является другой нормальной частотой ω2.

Если ω_I ≈ ω_II , |ω_I – ω_II | <<ω_I ≈ ω_{II ,} тогда отчетливо будут наблюдаться биения.Биение– колебание, которое происходит с медленой частотой и является суммой двух гармонических колебаний с близкими частотами. Это колебание с изменяющейся амплитудой. Оно лишь приблизительно гармоническое с частотой ω_I ≈ ω_II , а его амплитуда изменяется с частотой |ω_I – ω_II |.T_биен=2/(ω_I – ω_{II ).}

_Δω=ω_I – ω_II

<ω>=(ω_I +ω_II)/2

S₁(t)=2*S₁(t)*(cos( _Δω/2)t) *cos(<ω>t)

S₂(t)=2*S₁(t)*(sin( _Δω/2)t) *cos(<ω>t)